二次函数

二次函数

形如 \(y=ax^2+bx+c\) 的函数（\(a\neq 0\)）。

\(y=x^2\) 的图像是一条抛物线，开口向上，关于 \(y\) 轴对称，最低点是图像与对称轴的交点。

为什么对称？

首先，我们容易发现图像一定在 \(x\) 上方。

要满足对称，就是要满足对应点的连线被对称轴垂直平分。

考虑对于 \(x(x\geq 0)\) ，二次函数的函数值是 \(x^2\) ，对于 \(-x\) ，二次函数的函数值仍是 \(x^2\) 。

所以我们发现对于 \(x\) ，\(x\) 和 \(-x\) 的函数值一样。

这就代表直线 \(x\) 与 \(y=x^2\) 的交点 \(a\) ，直线 \(-x\) 与 \(y=(-x)^2\) 的交点 \(a'\) ，有 \(aa'\) 垂直于 \(y\) 轴。（三线合一）

平分易证。

下面是 \(y=-x^2\) 的图像。

显然就是将 \(y=x^2\) 的图像关于 \(x\) 轴对称了一下。

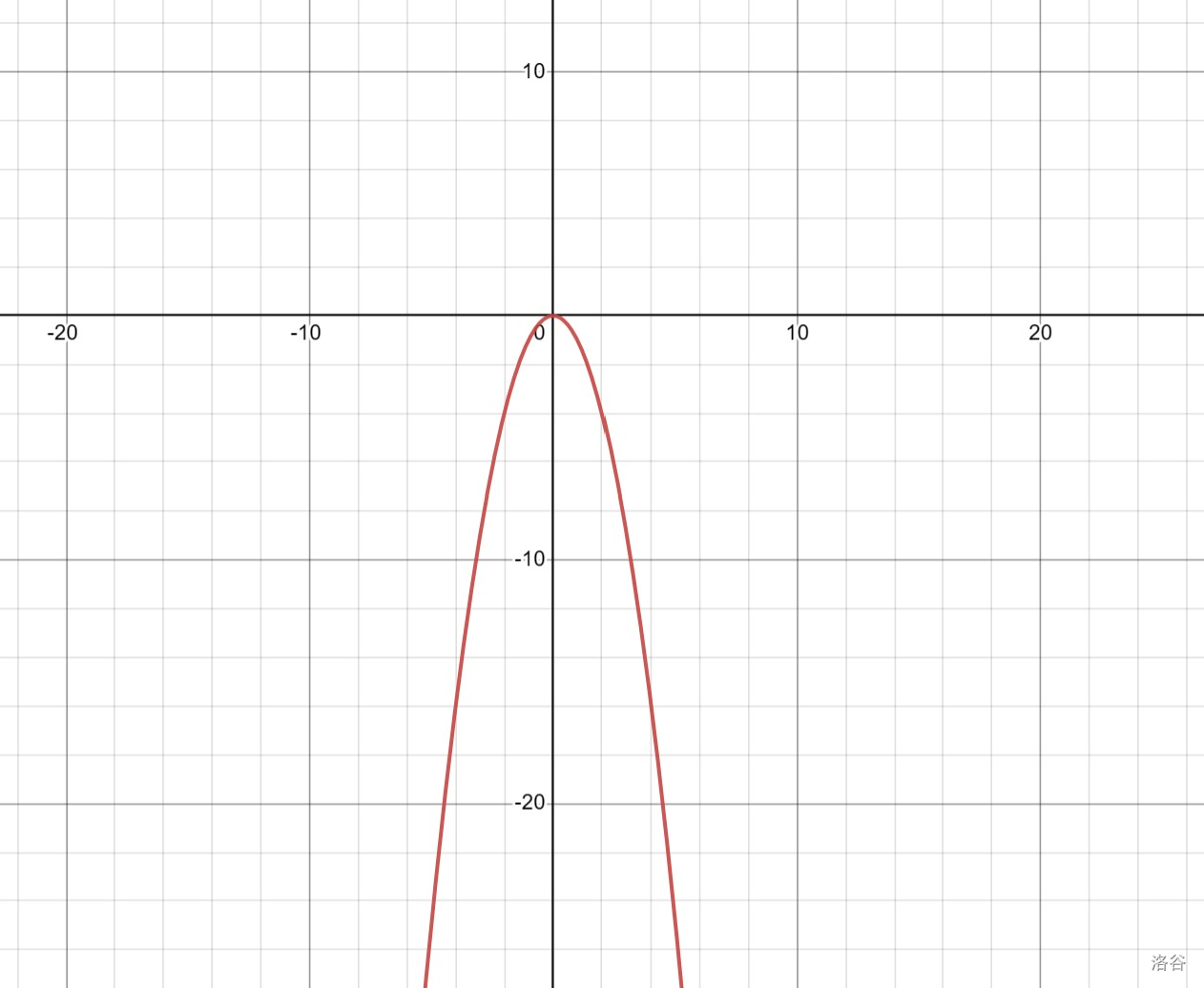
我们又可以证明 \(y=x^2\) 与 \(y=-x^2\) 关于原点成中心对称。

证明其实就是找一组点的关系。

接下来研究 \(y=ax^2\) 的这条图像。

一般的，二次函数 \(y=ax^2\) 的图象是抛物线。我们把二次函数 \(y=ax^2\) 的图像叫做 \(y=ax^2\)

我们发现，对于 \(y=x^2\) 的这条抛物线， \(y=ax^2\) 本质上就是对于对应点 \(x\) 和 \(-x\) ，将其对应的函数值 \(\times a\) （废话） 。这是两者的函数值仍然相等，仍然是轴对称图形，性质没有发生变化。

如果我们借助 Desmos 找到 \(y=ax^2\) 的图像，我们可以发现，函数的开口窄度与 \(a\) 成正比例。

即：随着 \(a\) 的增大，函数开口越来越窄。

这个也容易发现。因为对于 同一个 \(x\) ，当 \(a\) 增大时，\(y\) 也增大，于是在第一象限内的函数的斜率越来越大，整个函数开口越来越小。

抛物线 \(y=ax^2\) 的对称轴是 \(y\) 轴，顶点是原点，当 \(a>0\) 时，开口向上，顶点是最低点，反之亦然。

这个则是由于我们刚才发现 \(y=ax^2\) 相对于 \(y=x^2\) 的性质没有发生变化。

对于 \(y=ax^2+k\) ，，我们利用函数的基本知识可以发现就是将图像向上平移了 \(k\) 个单位，顶点变为 \((0,k)\) 。

请读者自证。

接下来研究 \(y=a(x+k)^2\) 。借助 Desmos ，我们可以发现：

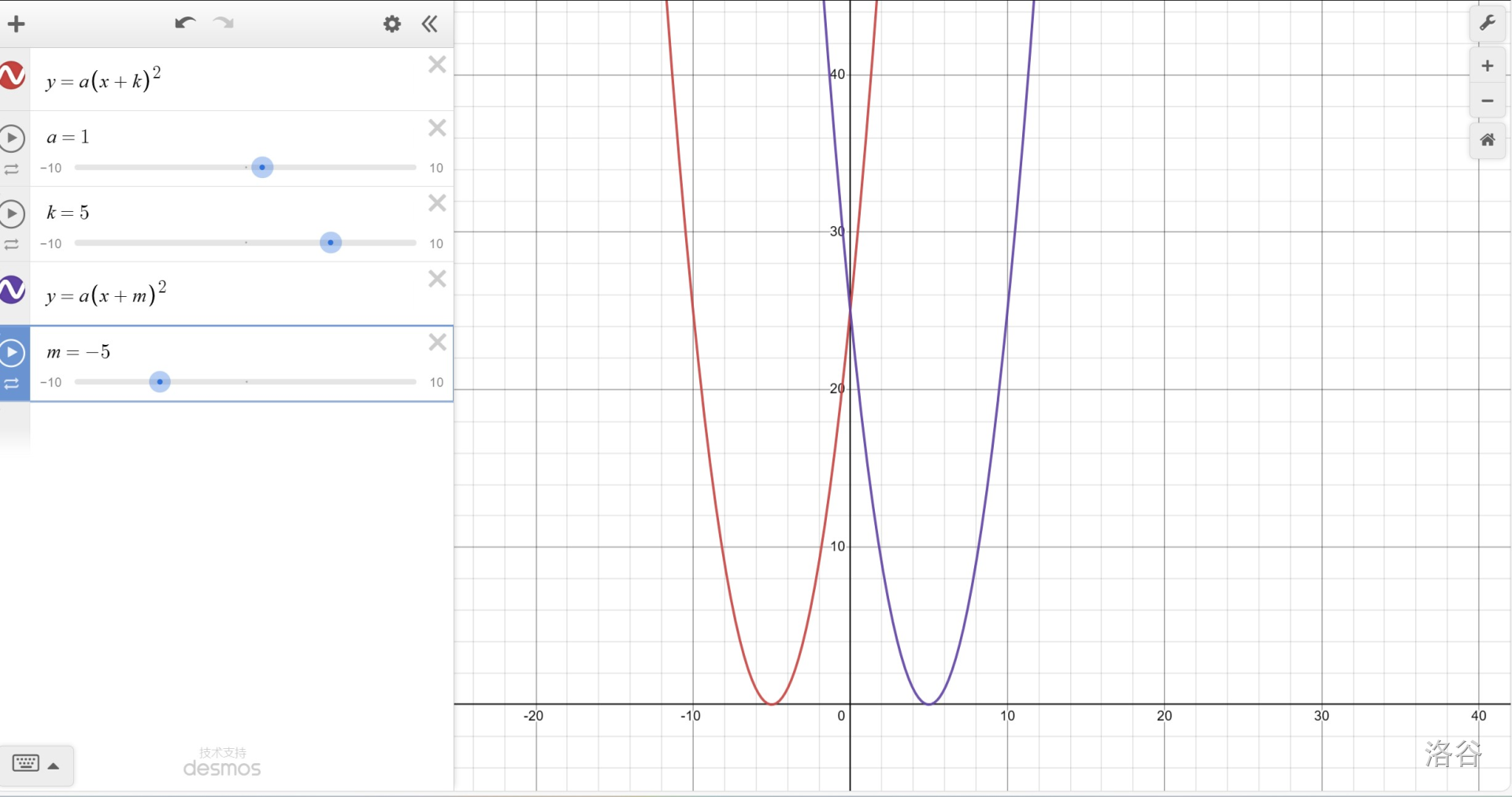
数学直觉告诉我们 \(y=(x+5)^2\) 与 \(y=(x-5)^2\) 可以看作由 \(y=x^2\) 平移得到。

确实是这样的。

因为对于同一个 \(x\) ，函数值变成了 \((x+5)^2\) ，使得该点比原来更向上，可以看作向上平移 \(10x+25\) 得到。

那么往哪平移？

容易发现，对于 \(y=a(x+k)^2\) ，当 \(k>0\) 时，其可以视作由 \(y=ax^2\) 向左平移 \(k\) 个单位得到，因为对于 \(x-k\) ，其函数值才为 \(0\) 。

其余性质与 \(y=ax^2\) 一致。

现在研究 \(y=a(x-h)^2+k\) 。

借助类比，我们可以发现 \(y=a(x+h)^2+k\) 可以视作由 \(y=a(x+h)^2\) 向上平移 \(k\) 个单位得到。而 \(y=a(x+h)^2\) 又可以视作由 \(y=ax^2\) 向左平移 \(h\) 个单位得到，所以 \(y=a(x+h)^2+k\) 可以视作由 \(y=ax^2\) 向左上平移得到。

记住口诀：上加下减，左加右减。

我们发现：

\[ax^2+bx+k=ax^2+2a\times \frac{b}{2a}\times x+a\times (\frac{b}{2a})^2+[k-a\times (\frac{b}{2a})^2]=a[x^2+2\times \frac{b}{2a}\times x+(\frac{b}{2a})^2]+k-a\times (\frac{b}{2a})^2=a(x+\frac{b}{2a})^2+k-a\times (\frac{b}{2a})^2 \]

令 \(h=\frac{b}{2a}\) ，\(p=k-a\times(\frac{b}{2a})^2\) 。

于是，\(ax^2+bx+k=a(x+h)^2+k\) 。

我们经过困难的探索发现（反正笔者是推了 15min），对于所有形式的 \(ax^2+bx+k(a\neq 0)\) （\(a,b,k\) 为常数），都可以化为 \(a(x+h)^2+p\) ，其中 \(h,p\) 是常数，未知数只有 \(x\) 。

所以根据上面得出的 \(y=a(x+h)^2+k\) 的相关性质，我们就可以得到 \(y=ax^2+bx+c\) 的相关性质：

对于抛物线 \(y=ax^2+bx+k\) ，其是轴对称图形，对称轴是一条平行于 \(y\) 轴的直线 \(x=-\frac{b}{2a}\)。抛物线的开口方向取决于 \(a\) ，当 \(a>0\) 时，开口朝上，反之朝下。抛物线可以看作是由 \(y=ax^2\) 向左平移 \(\frac{b}{2a}\) ，向上平移 \(k-a\times(\frac{b}{2a})^2\) 得到，顶点为 \((-\frac{b}{2a},k-a\times(\frac{b}{2a})^2)\) 。

关于顶点，还可以表示为 \((-\frac{b}{2a},\frac{4ak-b^2}{4a})\) ，通过化简可以发现和上面的顶点式等价。

upd：\((-\frac{b}{2a},\frac{4ac-b^2}{4a})\) 是教科书上常用的顶点式，具体推导过程如下：

\(ax^2+bx+c=a\times (x^2+\frac{b}{a}x)+c=a[x^2+2\times \frac{b}{2a}x+(\frac{b}{2a})^2-(\frac{b}{2a})^2]+c=a(x+\frac{b}{2a})^2+\frac{4ac-b^2}{4a}\)

其实就是配方。笔者采取先配方后提项，而教科书采用了相反的方法。

我们已经研究完了二次函数的性质！

确定表达式

我们直接开始研究普遍性的给出不共线三点求出二次函数表达式的问题。

普遍性指三点不具有任何的性质。

设给出的三点为 \((u_1,v_1),(u_2,v_2),(u_3,v_3)\) ，求出经过该三点的二次函数表达式。

不妨设抛物线 \(y=ax^2+bx+c\) 。于是我们将坐标带入，发现：

\(\begin{cases} v_1=a{u_1}^2+bu_1+c\\ v_2=a{u_2}^2+bu_2+c\\v_3=a{u_3}^2+bu_3+c\end{cases}\)

可以发现这是一个很简单的三元一次方程组，消元法来解即可。

与一元二次方程的关系

对于 \(y=ax^2+bx+c\) ，当 \(y=0\) 时，就是关于 \(x\) 的一元二次方程 \(ax^2+bx+c=0\) 的解。

当 \(y=ax^2+bx+c\) 与 \(y=0\) 有两个交点时，代表二次方程有两个实数解；一个交点时，代表有一个实数解；没有交点则代表无实数解。

于是，我们逆向考虑一下，可以通过判断二次方程 \(ax^2+bx+c=0\) 的实数解个数，来判断 \(y=ax^2+bx+c\) 与 \(y=0\) 的交点数。而前者可以通过判断 \(b^2-4ac\) 的正负来判断。

同样，我们可以通过“夹逼”的方法来求二次方程的近似解。