![]()
1 /*
2 POJ2480 Longge's problem
3 http://poj.org/problem?id=2480
4 数论 欧拉函数 线性筛
5
6 求sigma_i=1^n{gcd(i,n)}
7 <=>sigma_d|n{d*phi(n/d)}
8 *
9 *
10 *
11 *
12 */
13 #include <cstdio>
14 #include <algorithm>
15 #include <cmath>
16 #define new
17 #ifdef OLD
18 //250ms
19 using namespace std;
20 const long long Nmax=1000005LL;
21 long long n;
22 int is_prime[Nmax];
23 int prime[Nmax];
24 int cnt;
25 long long phi[Nmax];
26 long long oula(long long n)
27 {
28 if(n==1LL)
29 return 1LL;
30 if(n<Nmax)
31 return phi[n];
32 long long ret=1LL,i;
33 for(i=2LL;i*i<=n;i++)
34 {
35 if(n%i==0LL)
36 {
37 n/=i,ret*=i-1LL;
38 while(n%i==0LL) n/=i,ret*=i;
39 }
40 }
41 if(n>1LL) ret*=n-1LL;
42 return ret;
43 }
44
45 void get()
46 {
47 for(int i=2;i<Nmax;i++)
48 is_prime[i]=1;
49 for(long long i=2;i<Nmax;i++)
50 {
51 if(is_prime[i])
52 {
53 prime[++cnt]=i;
54 phi[i]=(long long)(i-1);
55 }
56 for(int j=1;j<=cnt;j++)
57 {
58 if(i*prime[j]>=Nmax)
59 break;
60 is_prime[i*prime[j]]=0;
61 if(i%prime[j]==0)
62 {
63 phi[i*prime[j]]=phi[i]*(long long)prime[j];
64 break;
65 }
66 else
67 phi[i*prime[j]]=phi[i]*(long long)(prime[j]-1);
68 }
69 }
70 }
71
72 int main()
73 {
74 // freopen("1.in","r",stdin);
75 //scanf("%lld%lld",&a,&b);
76 //printf("%lld\n",gcd(a,b));
77 get();
78 while(scanf("%lld",&n)==1)
79 {
80 //n=read();
81 //printf("%lld\n",n);
82 //if(n==0LL)
83 //break;
84 if(n<Nmax && is_prime[n])
85 {
86 printf("%lld\n",2LL*n-1LL);
87 continue;
88 }
89 long long ans=0LL;
90 for(long long i=1LL;i*i<=n;i++)
91 {
92 if(n%i==0LL)
93 ans+=i*oula(n/i)+n/i*oula(i);
94 if(i*i==n)
95 ans-=i*oula(n/i);
96 }
97 printf("%lld\n",ans);
98 }
99
100 //for(long long n=1;n<=100;n++)
101 //{
102 //long long ans=0LL;
103 //for(long long i=1LL;i<=n;i++)
104 //ans+=gcd(i,n);
105 //printf("%d:%d\n",n,ans);
106 //long long m=n;
107 ////for(long long i=1;prime[i])
108 //}
109 return 0;
110 }
111
112 #endif
113
114 #ifdef new
115 //32ms
116
117 using namespace std;
118 int main()
119 {
120 long long n;
121 while (scanf("%lld", &n) != EOF)
122 {
123 long long i, sqr, p, a, ans;
124 ans = n;
125 sqr = floor(sqrt(n*1.0));
126 for (i = 2; i <= sqr; i++)
127 {
128 if (n%i == 0)
129 {
130 a = 0;
131 p = i;
132 while (n%p == 0)
133 {
134 a++;
135 n /= p;
136 }
137 sqr = floor(sqrt(n*1.0));
138 ans = ans + ans*a*(p-1)/p;
139 }
140 }
141 if (n!=1)
142 ans = ans + ans*(n-1)/n;
143 printf("%lld\n", ans);
144 }
145 return 0;
146 }
147
148 #endif
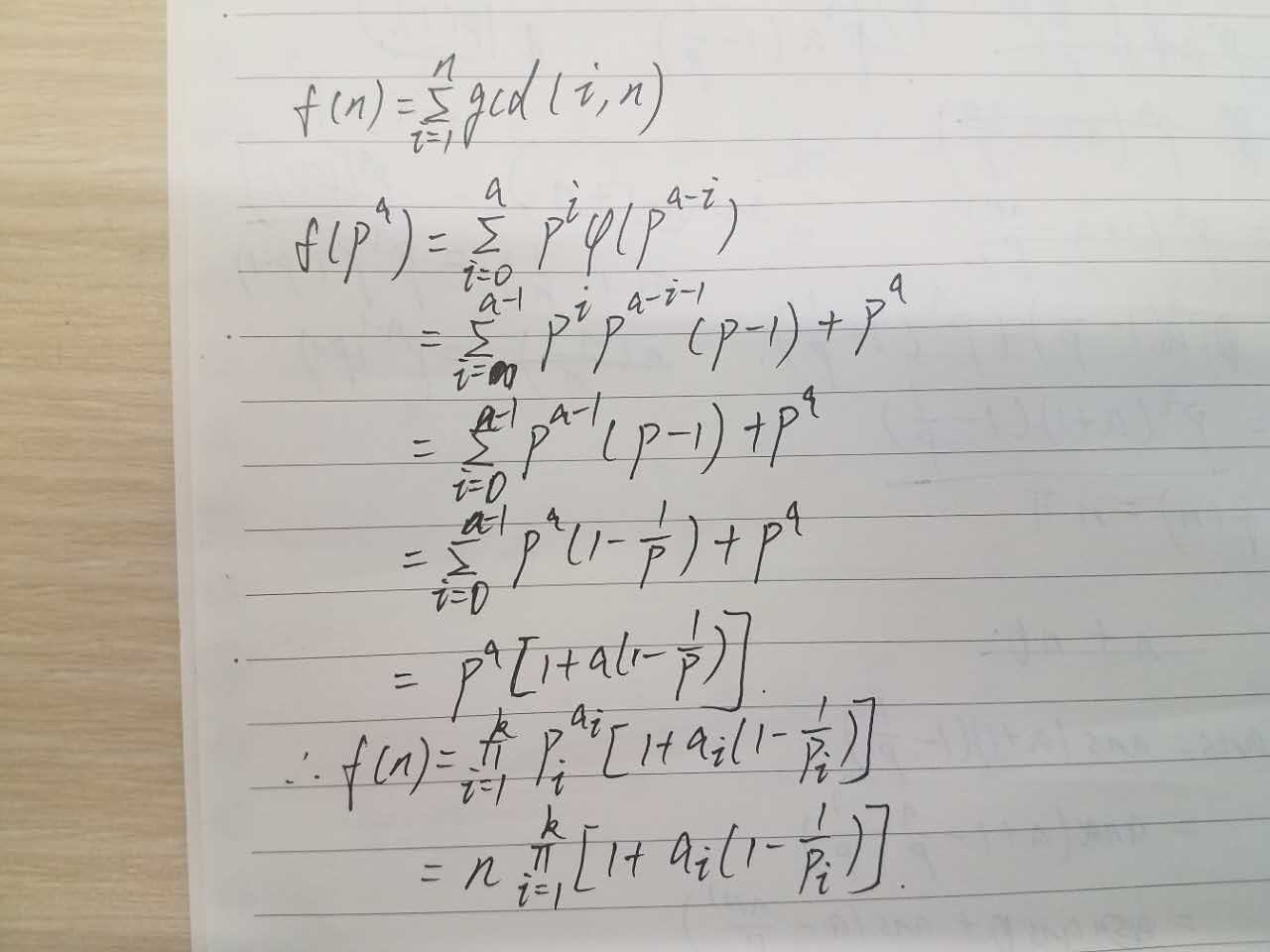

 浙公网安备 33010602011771号
浙公网安备 33010602011771号