1. 问题描述：

　　设集合x，集合y，集合元素若干，求x和y的最长公共子序列。（子序列：给定一个序列，该序列中删去若干元素后得到的序列）

 

备注：

 

  • 　　编程语言：c++
  • 　　编译器：Code::Blocks 16.01
  • 　　操作系统：windows 10

 

源代码：

  1 //最长公共子序列
  2 
  3 /*测试数据
  4 7 6
  5 A B C B D A B
  6 B D C A B A
  7 */
  8 
  9 #include<iostream>
 10 
 11 using namespace std;
 12 
 13 //计算最长公共子序列长度的动态规划算法LSCLength
 14 void LCSLength(int m,int n,char *x,char *y,int **c,int **b)
 15 {
 16     int i,j;
 17     for(i=1; i <= m; i++)
 18         c[i][0] = 0;
 19     for(i=1; i <= n;i++)
 20         c[0][i] = 0;
 21     for(i=1; i <= m; i++)
 22     {
 23         for(j=1; j <= m; j++)
 24         {
 25             if(x[i] == y[j])
 26             {
 27                 c[i][j] = c[i-1][j-1]+1;  //子问题1：c[i][j]值等于斜上方的长度加1
 28                 b[i][j] = 1;
 29             }
 30             else if(c[i-1][j] >= c[i][j-1])
 31             {
 32                 c[i][j] = c[i-1][j];  //子问题2：c[i][j]值等于上面的长度
 33                 b[i][j] = 2;
 34             }
 35             else
 36             {
 37                 c[i][j] = c[i][j-1];  //子问题3：c[i][j]值等于左面的长度
 38                 b[i][j] = 3;
 39             }
 40         }
 41     }
 42 }
 43 
 44 //LCS实现根据b的内容打印出x和y最长公共子序列
 45 void LCS(int i,int j,char *x,int **b)
 46 {
 47     if(i==0 || j==0)
 48         return;
 49     if(b[i][j] == 1)
 50     {
 51         LCS(i-1,j-1,x,b);
 52         cout<<x[i];
 53     }
 54     else if(b[i][j] == 2)
 55         LCS(i-1,j,x,b);
 56     else
 57         LCS(i,j-1,x,b);
 58 }
 59 
 60 int main()
 61 {
 62     int mm,nn;  //mm：xx集合元素个数  yy集合元素个数
 63     char *xx,*yy;
 64     int **cc,**bb;
 65 
 66     cout<<"分别输入x和y集合元素个数："<<endl;
 67     cin>>mm>>nn;
 68 
 69     xx = new char[mm+1];  //xx集合
 70     yy = new char[nn+1];  //yy集合
 71     //输入数据
 72     cout<<"x集合元素："<<endl;
 73     for(int r=1;r<=mm;r++)
 74         cin>>xx[r];
 75     cout<<"y集合元素："<<endl;
 76     for(int r=1;r<=nn;r++)
 77         cin>>yy[r];
 78 
 79     //创建动态二维数组
 80     cc = new int*[mm+1];  //cc[i][j]存储xx和yy的最长公共子序列的长度
 81     bb = new int*[mm+1];  //bb[i][j]记录cc[i][j]的值是由哪个子问题得到的
 82     /*子问题：
 83     1--cc[i][j] = cc[i-1][j-1]+1  （斜上方的长度加1）
 84     2--cc[i][j] = cc[i-1][j]  （等于上面的长度）
 85     3--cc[i][j] = cc[i][j-1]  （等于左边的长度）
 86     */
 87     for(int i=0;i<=mm; i++)
 88     {
 89         cc[i] = new int[nn];
 90         bb[i] = new int[nn];
 91     }
 92 
 93     //赋初值
 94     for(int j=0;j<=mm;j++)
 95     {
 96         for(int k=0;k<=nn;k++)
 97         {
 98             cc[j][k]=-1;
 99             bb[j][k]=-1;
100         }
101     }
102 
103     cout<<endl;
104     LCSLength(mm,nn,xx,yy,cc,bb);
105 
106     //输出二维数组
107     cout<<"c[i][j]存储x和y的最长公共子序列的长度："<<endl;
108     for(int j=0;j<=mm;j++)  //输出cc[i][j]，cc[i][j]存储xx和yy的最长公共子序列的长度
109     {
110         for(int k=0;k<=nn;k++)
111             cout<<cc[j][k]<<"\t";
112         cout<<endl;
113     }
114     cout<<endl;
115 
116     cout<<"b[i][j]记录c[i][j]的值是由哪个子问题得到的："<<endl;
117     cout<<"1--cc[i][j] = cc[i-1][j-1]+1  （斜上方的长度加1）"<<endl;
118     cout<<"2--cc[i][j] = cc[i-1][j]  （等于上面的长度）"<<endl;
119     cout<<"3--cc[i][j] = cc[i][j-1]  （等于左边的长度）"<<endl;
120     for(int j=0;j<=mm;j++)  //输出bb[i][j]，bb[i][j]记录cc[i][j]的值是由哪个子问题得到的
121     {
122         for(int k=0;k<=nn;k++)
123             cout<<bb[j][k]<<"\t";
124         cout<<endl;
125     }
126 
127     cout<<endl;
128     cout<<"最长公共子序列：";
129     LCS(mm,nn,xx,bb);
130     cout<<endl;
131 
132     //释放空间
133     delete[] xx;
134     delete[] yy;
135 
136     for(int i=0;i<=nn;i++)
137     {
138         delete[] cc[i];
139         delete[] bb[i];
140     }
141     delete[] cc;
142     delete[] bb;
143 
144     return 0;
145 }

 

 

 

 
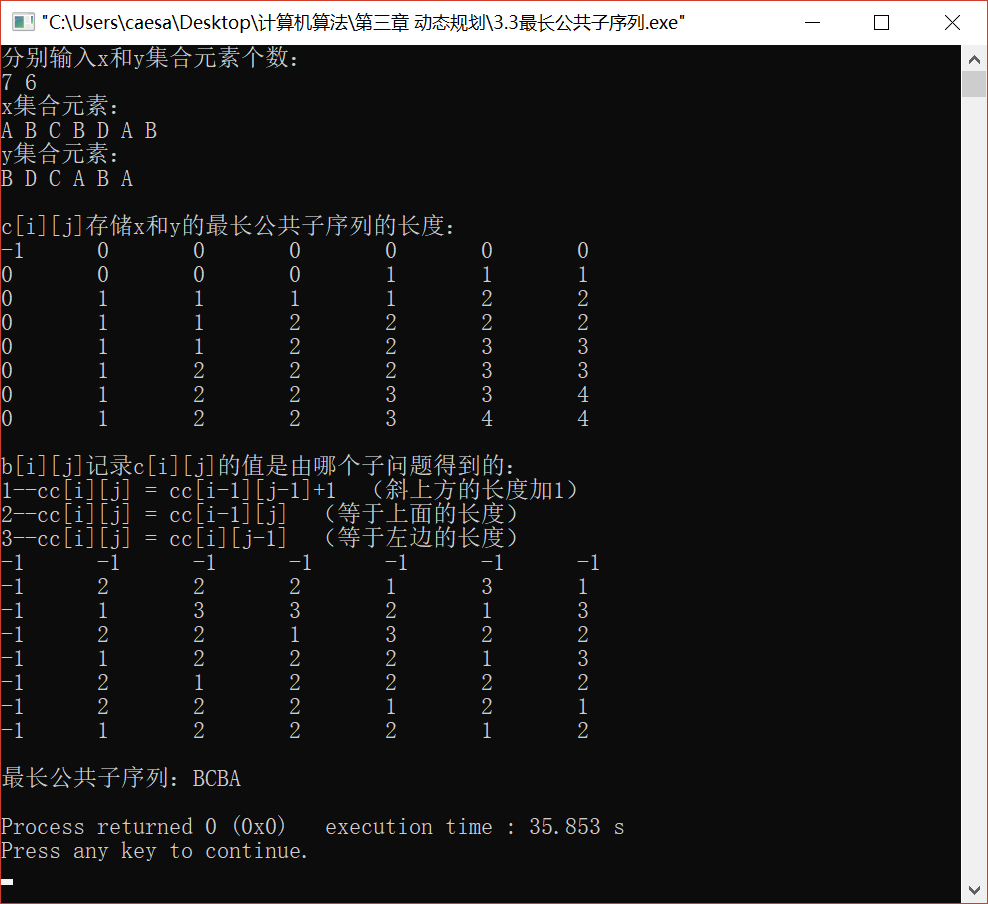
运行界面：