Let’s Get Married

http://acm.hdu.edu.cn/showproblem.php?pid=6912

 

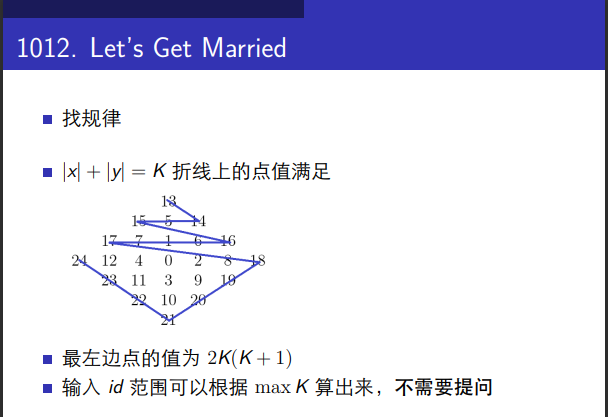
 1.2*k(k+1) ,k代表层数，找规律发现如果一个点的坐标为

2.（x,y)且|x|+|y|=k，id<=2*k*(k+1)

如果给我们的是id,那么我们二分出该值所在层数，然后这里有个技巧我们吧该值减去上一层最大的值，就可以把id小化，同时方便计算左边，

正因为这个处理，我们发现在x周上方的点是左右对称放置的，很容易得到坐标，剩下两个象限里的点，则是按照斜对角变化的，

第三象限的是从左上到右下依次递减，第四象限的则是从左下到右上依次递减。然后在坐标轴上的点即为id-f(n-1).

针对操作二给出坐标求值，就需要用到结论2，先确定上一层的最大值

#include<iostream>
#include<cmath>
#include<cstdio>
using namespace std;
typedef long long ll;
ll nowx,nowy;


ll f(ll x)//返回当前层大的的元素
{
    if(x<=0)
        return 0;
    return 2*(1+x)*x;
}

int find(ll id)//二分查找层数
{
    ll l=0,r=1e9;
    while(l<r)
    {
        ll mid=(l+r)>>1;
        if(f(mid)>=id)
            r=mid;
        else
            l=mid+1;
    }
    return l;
}


void slove1(ll id)
{
    ll n=find(id);
    id-=f(n-1);
    ll x,y;
    if(id==0)
        x=0,y=0;//原点
    else if(id==1)
        x=0,y=n;//y轴上
    else if(id<=2*n-1) //x轴上方
    {
        ll t=id/2;
        ll r=id%2;//判断奇偶数
        if(!r)
            x=t,y=n-t;
        else
            x=-t,y=n-t;
    }
    else if(id<=3*n)
    {
        id-=2*n;
        y=-id;
        x=n-id;
    }
    else if(id<=4*n)
    {
        id-=3*n;
        x=-id;
        y=-(n-id);
    }
     printf("%lld %lld\n",x-nowx,y-nowy);
    nowx=x,nowy=y;
}
void solve2(ll x,ll y)
{
    ll n=abs(x)+abs(y); // |x|+|y|=k,该层最左边的值为2*k*(k+1);
    ll id;
    id=f(n-1);
    if(y>0)
    {
        if(x>0)
            id+=2*abs(x);
        else
            id+=2*abs(x)+1;
    }
    else
    {
        if(x>=0)
            id+=2*n+abs(y);
        else
            id+=3*n+abs(x);
    }
    if(n==0)
        id=0;
     printf("%lld\n",id);
    nowx=x,nowy=y;
}

int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        int op;
        cin>>op;
        if(op==1)
        {
            ll id;
            cin>>id;
            slove1(id);
        }
        else
        {
            ll x,y;
            cin>>x>>y;
            solve2(x,y);
        }

    }
    return 0;
}