2021.10.16

T1:Makik 的能量项链

Problem:

Makik 有一串能量项链，这串项链是从 Mars 母星带来的，作为祖传之宝一直陪伴他。这个项链有 n个能量珠，每个能量珠有一个属性值。于是这 n 个能量珠一共有 k 种属性值（即可能有多个能量珠有同一种属性）。现在 Makik 可以通过特殊的拆解方式，拆解两个位置，使得这一圈能量珠变为两条链状结构。

但是拆解后的能量珠可能会不稳定。Makik 发现当且仅当拆解后的两条链中，没有相同属性的能量珠时，才是稳定结构。

Makik 想知道有多少种拆解方式，以及两条链的长度差的绝对值的最小值。

Solution:

考虑中间的十分，每种颜色值出现了两次

我们可以在一种颜色出现第一次的时候 +1， 出现第二次的时候 -1

那么前缀和相等的一对点一定可以成为一对分割点

如果颜色出现了不止一次的话，+1，-1显然不行

所以我们可以每次加减一个不同的很大整数来避免重复

Code:

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+100;
typedef unsigned long long ull;
typedef long long LL;
const ull base1=19941007;
const ull base2=1321;
int n,k,ans,cnt;
int a[N<<1];
int t[N],temp[N];
int Abs(int x){
    return x<0?-x:x;
}
void force(){
    ans=n;
    for(int i=1;i<=n;++i){
        scanf("%d",&a[i]);
        a[i+n]=a[i];
        t[a[i]]++;
    }
    int flag=1;
    for(int i=1;i<=n;++i){
        for(int j=i;j<=n*2;++j){
            flag=1;
            for(int s=i;s<=j;++s) temp[a[s]]++;
            for(int s=1;s<=k;++s){
                if(temp[s]&&temp[s]!=t[s]){
                    flag=0;
                    break;
                }
            }
            if(flag&&!(j-i+1==n)){
                ans=min(ans,Abs(n-2*(j-i+1)));
                cnt++;
            }
            for(int s=i;s<=j;++s) temp[a[s]]--;
        }
    }
    printf("%d %d",cnt/2,ans);
}
ull Hash1[N],Hash2[N];
void Get_hash(int n){
    Hash1[0]=1;
    Hash2[0]=1;
    for(int i=1;i<=n;++i) Hash1[i]=Hash1[i-1]*base1;
    for(int i=1;i<=n;++i) Hash2[i]=Hash2[i-1]*base2;
}
int b[N];
struct hx{
    ull t1,t2;
    int pos;
    bool operator < (const hx &a) const { 
        if(t1!=a.t1) return t1<a.t1;
        else if(t2!=a.t2) return t2<a.t2;
        else return pos<a.pos;
    }
}T[N];
int main(){
    scanf("%d%d",&n,&k);
    Get_hash(k);
    for(int i=1;i<=n;++i) scanf("%d",&a[i]);
    for(int i=n;i>=1;--i) if(!b[a[i]]) b[a[i]]=i;
    ull s1=0,s2=0;
    for(int i=1;i<=n;++i){
        s1=s1+Hash1[a[i]];
        s2=s2+Hash2[a[i]];
        t[a[i]]++;
        if(b[a[i]]==i){
            s1=s1-Hash1[a[i]]*t[a[i]];
            s2=s2-Hash2[a[i]]*t[a[i]];
        }
        T[i].t1=s1;
        T[i].t2=s2;
        T[i].pos=i;
    }
    sort(T+1,T+1+n);
    LL cnt=0;
    int ans=n,l=1,r=0,ans1,ans2,i,j;
    int mid=(n+1)>>1;
    for(i=1;i<=n;++i){
        j=i;
        while(T[j].t1==T[i].t1&&T[j].t2==T[i].t2&&j<=n) j++; 
        cnt+=1LL*(j-i)*(j-i-1)/2;
        for(l=i,r=i;r<=j-1;r++){
            ans1=ans2=n;
            while(l<r&&T[r].pos-T[l].pos>=mid) l++;
            ans1=Abs(n-2*(T[r].pos-T[l].pos));
            if(l>i) ans2=Abs(n-2*(T[r].pos-T[l-1].pos));
            ans=min(ans,min(ans1,ans2));
        }
        i=j-1;
    }
    printf("%lld %d\n",cnt,ans);
    return 0;
}

T2:Makik 开飞机

Problem:

Makik 在达到世界首富之后，面对自己开遍全球的随处可见的富丽堂皇的金库巨大的银行感到索然无味，于是他买了一架私人定制飞机开始挑战极限：在地球的赤道进行一圈的飞行环游。当然他考虑过带着马仔驾驶飞机进行空中加油，但低调的他还是选择在赤道上自己开的飞机场加油。

现在给出你 Makik 在赤道开的 n 个飞机场，飞机场可以进行飞机的加油。

Makik 有 s 架飞机型号并且知道每种型号每次加油后最长的飞行距离 d，并向你询问每种型号包括最后一次降落加油的降落加油次数最少是多少

Solution:

思博题

倍长之后 O(n) 看一下每个点往后最大能到哪，向他连条边，这样就形成了一棵树

接下来的问题就变成普及组倍增/二分了

Code:

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=2000005;
int n,m,u,s[maxn],f[maxn],st[maxn];
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++){
        int x;
        scanf("%d",&x);
        if(u<x) u=x;
        s[i]=s[i-1]+x;
    }
    for(int i=n+1;i<=n+n;i++) s[i]=s[i-1]+s[i-n]-s[i-n-1];
    for(int i=1;i<=n;i++) st[i]=i,f[i]=0;
    while(m--){
        int d;
        scanf("%d",&d);
        if(d<u){
            puts("NIE");
            continue;
        }
        int j=1;
        for(int i=n+1;;i++){
            while(s[i]-s[j]>d) j++;
            f[i]=f[j]+1;
            st[i]=st[j];
            if(i-st[i]>=n){
                printf("%d\n",f[i]);
                break;
            }
        }
    }
    return 0;
}

T3:Makik 剩单

Problem:

Makik 有一棵圣诞树，这棵树非常巨大，上面满满的陈列着各种剩单礼物，一共有 n 个。

但是冬天到了，由于 Makik 本质是鸽子，所以忘记了浇水，于是整棵圣诞树只有树枝。从图论上看，这也是数学中的树形结构，巧的是，这棵树恰有 n 个节点，n-1 条边，且无环，每个礼物都挂在了节点上，节点之间有边相连通（即点和边构成的树形结构）。

现在 Makik 想知道其中优美圣诞结构的个数。

一个优美圣诞结构定义为：三个圣诞礼物两两之间的距离都相同的结构。

Solution:

很强的一个题，先考虑暴力

暴力01:对每个点都大力BFS，我觉得这个我不用讲

暴力02:树形 DP

考虑这样一个问题，要怎么样的点才能满足三个点两两距离相等呢？

1、存在三个点有共同的 lca。

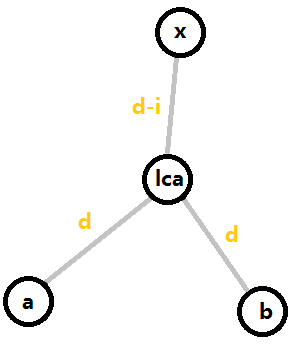
2、存在一个点，使得它到它两颗不同的子树种两点的距离为 d 且它存在 d 级祖先。

大力 DP

f(x,i) 表示以 x 为根的子树中，距离 x 为 i 的点数

g(x,i) 表示以 x 为根的子树中, 形如下图的的 (a,b) 数量

 

其中 d 可以是任意值（说白了就是都考虑进去），或者说只要在上面街上一个长度为 i 的边就可以构成一个合法的三元组。

考虑转移，枚举 x 的下一个儿子 u

g(x,i) += f(x,i)\times f(u,i-1) + g(u,i+1)

f(x,i) += f(u,i-1)

Code:

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=100010;
struct vec{
    int to;
    int fro;
}mp[maxn*2];
int tai[maxn],cnt;
ll memp[maxn*5];
ll *f[maxn],*g[maxn];
int mx[maxn];
int dep[maxn];
ll *wzh=memp+5;
int n;
ll ans;
inline void be(int x,int y){
    mp[++cnt].to=y;
    mp[cnt].fro=tai[x];
    tai[x]=cnt;
}
inline void bde(int x,int y){
    be(x,y);
    be(y,x);
}
void dfs1(int x,int F){
    int i,y;
    mx[x]=x;
    for(i=tai[x];i;i=mp[i].fro){
        y=mp[i].to;
        if(y!=F){
            dep[y]=dep[x]+1;
            dfs1(y,x);
            if(dep[mx[y]]>dep[mx[x]]){
                mx[x]=mx[y];
            }
        }
    }
    for(i=tai[x];i;i=mp[i].fro){
        y=mp[i].to;
        if(y!=F&&(mx[y]!=mx[x]||x==1)){
            y=mx[y];
            wzh+=dep[y]-dep[x]+1;
            f[y]=wzh;
            g[y]=(wzh+=1);
            wzh+=(dep[y]-dep[x])*2+1;
        }
    }
}
void dp(int x,int F){
    int i,j,y,z;
    for(i=tai[x];i;i=mp[i].fro){
        y=mp[i].to;
        if(y==F) continue ;
        dp(y,x);
        if(mx[y]==mx[x]){
            f[x]=f[y]-1;
            g[x]=g[y]+1;
        }
    }
    ans+=g[x][0];
    f[x][0]=1;
    for(i=tai[x];i;i=mp[i].fro){
        y=mp[i].to;
        if(y==F||mx[y]==mx[x]) continue ;
        for(j=0;j<=dep[mx[y]]-dep[x];j++){
            ans+=f[x][j-1]*g[y][j]+g[x][j+1]*f[y][j];
        }
        for(j=0;j<=dep[mx[y]]-dep[x];j++){
            g[x][j-1]+=g[y][j];
            g[x][j+1]+=f[x][j+1]*f[y][j];
            f[x][j+1]+=f[y][j];
        }
    }
}
int main(){
    int i,x,y;
    scanf("%d",&n);
    for(i=1;i<n;i++){
        scanf("%d%d",&x,&y);
        bde(x,y);
    }
    while(wzh!=memp){
        *wzh=0;
        wzh--;
    }
    *wzh=0;
    wzh+=1;
    dep[1]=1;
    dfs1(1,0);
    dp(1,0);
    printf("%lld\n",ans);
    return 0;
}