LGJOI20231012

还行的一场。

A

考虑一个 \(n \times n\) 的矩阵 \(A\)，初始所有元素为 \(0\)。

进行 \(q\) 次操作，每次操作给定参数 \(r, c, l, s\)，将 \(A\) 中左上顶点为 \(r, c\)，直角边长为 \(l\) 的下三角区域加上 \(s\)。

求最终矩阵的元素异或和。

solution:

如果是矩形区域很好做，二维差分即可。

现在只是变成了直角三角形，所以也往差分方向想。

暴力模拟操作，每次输出二维差分数组，可以得到类似这样的东西。

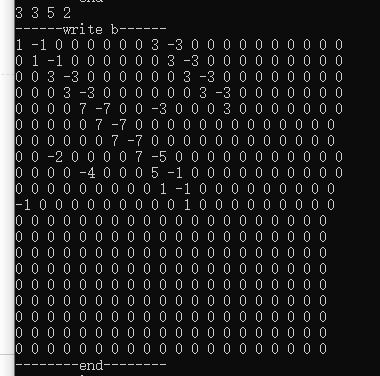
好多信息在斜线上，看起来很难维护。

于是考虑将斜线上的信息转化到直线上。

因为这题求的是三角矩阵，所以模仿着二位前缀和的定义，定义“二维三角前缀和”为每个点左上角的三角形区域的值的和。

int getsum(){
	for(int i = 1; i <= n; i ++)
		for(int j = 1; j <= n; j ++)
			if(i >= 2) a[i][j] = a[i - 1][j] + a[i - 1][j - 1] - a[i - 2][j - 1] + b[i][j];
		    	else a[i][j] = a[i - 1][j] + a[i - 1][j - 1] + b[i][j];
	return 0;
}
int getdel(){
	for(int i = 1; i <= n; i ++)
		for(int j = 1; j <= n; j ++)
			if(i >= 2){b[i][j] = a[i][j] - a[i - 1][j - 1] - a[i - 1][j] + a[i - 2][j - 1];}
			     else b[i][j] = a[i][j] - a[i - 1][j - 1] - a[i - 1][j];
	return 0;
}

像这样进行前缀和和差分即可完成上三角的前缀和。

那么再次尝试输出下差分数组得到：

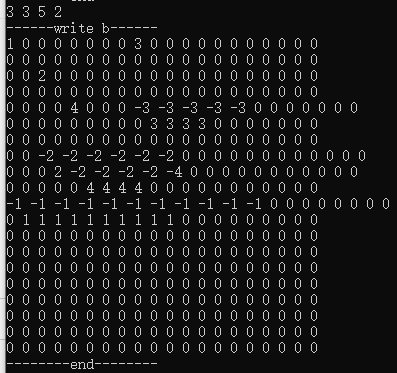
我们发现我们成功把信息转化到了直线上。

对每行再做一次差分，即可维护整个差分数组，最后用三角前缀和反推回去即可。

code

#include<iostream>
#include<fstream>
#include<algorithm>
#define int long long
using namespace std;
int n, N, q, ans;
int s[2050][2050];
int b[2050][2050];
int getsum(){
	for(int i = 1; i <= N; i ++){
		for(int j = 1; j <= N; j ++){
			if(i >= 2)
				b[i][j] = b[i - 1][j] + b[i - 1][j - 1] - b[i - 2][j - 1] + s[i][j];
			else b[i][j] = b[i - 1][j] + b[i - 1][j - 1] + s[i][j];
		}
	}
	return 0;
}
signed main(){
	cin >> n >> q;
	N = n * 2 + 3;
	while(q --){
		int x, y, l, S;
		cin >> x >> y >> l >> S;
		s[x][y] += S, s[x][y + 1] -= S;
		s[x + l][y] -= S, s[x + l][y + l + 1] += S;
		s[x + l + 1][y + 1] += S, s[x + l + 1][y + l + 1] -= S;
	}
	for(int i = 1; i <= N; i ++){
		for(int j = 1; j <= N; j ++)
			s[i][j] = s[i][j - 1] + s[i][j];
	}
	getsum();
	for(int i = 1; i <= n; i ++){
		for(int j = 1; j <= n; j ++)
			ans = ans ^ b[i][j]; 
	}
	cout << ans;
	return 0;
}

---

B

\(\text{Alice}\) 和 \(\text{Bob}\) 玩游戏。

1. \(\text{Alice}\) 先手，\(\text{Bob}\) 后手，轮流进行操作。有一个集合初始为 \(S = \left \{a_1, a_2, \cdots, a_n \right \}\)。

2. 第 \(i\) 轮操作有一个参数 \(b_i\) ……

晚上补。