P5014 水の三角(修改版)

题如其名 2.0。

水の三角(修改版)

这个三角图真好看。。

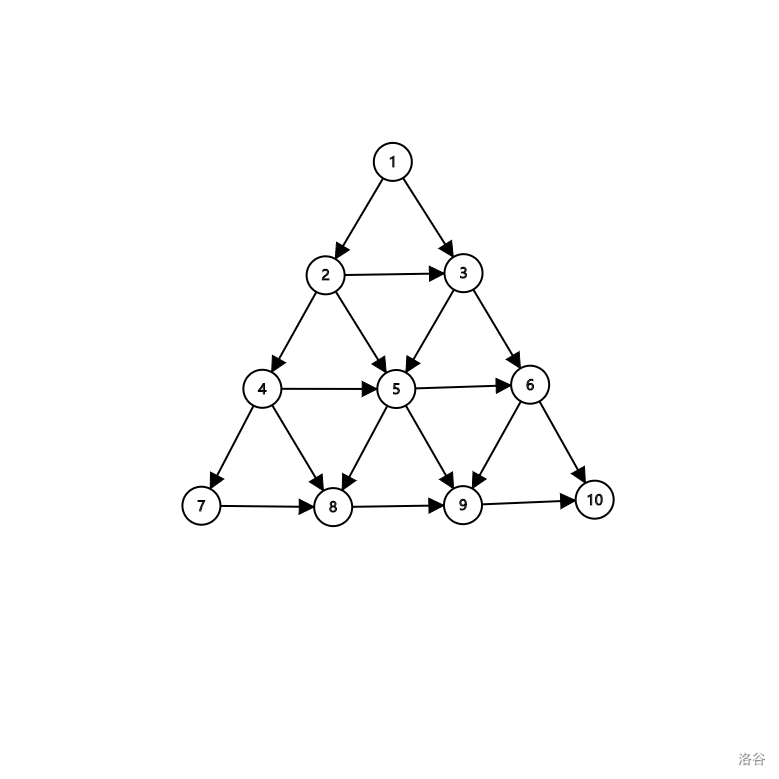
这个是 \({\rm 4}\) 阶三角图。

现在我们定义一个三角图是像上面一样的图。

请求出一个无限大的三角图从 \(1\) 号点走到 \(u\) 号点的方案数。

有 \(T\) 组询问。

\(1 \leq T \leq 100, \qquad 1 \leq u_i \leq 500000500000\)

这个三角图还真不一定好看。。

所以我们把它转化成坐标。定义坐标 \((n, m)\) 表示的是原图第 \(n + 1\) 行的第 \(m + 1\) 个数。将输入的点 \(u\) 转化为 \((n, m)\) ，一定有 \(n \ge m\)，且对于原题的数据范围，\(n, m \le 1e6\)。

然后问题转化成从坐标 \((0, 0)\) 走到 \((n, m)\)，每一步可以向 \((0, 1), (1,0), (1, 1)\) 三个方向走一格，且不能穿过直线 \(y = x\)，求方案数。

如果没有 \((1, 1)\) 这个方向，那么很好用卡特兰数做，见 P1641。表示方案数的式子是：

\[\binom{n + m}{m} - \binom{n + m}{m - 1} \]

考虑加上 \((1, 1)\) 这个方向怎么做。我们发现如果我们走这个方向，那么这一步一定不会穿过 \(y = x\)，因为这条路径本身就与 \(y = x\) 平行。

那很好办。枚举走 \((1, 1)\) 这个方向的步数 \(i\)。

先不考虑这么走的影响，那么将横纵坐标都向原点方向平移 \(i\) 个单位，然后得到只是横纵走的方案数是：

\[\binom{n + m - 2i}{m - i} - \binom{n + m - 2i}{m - i - 1} \]

然后加上向 \((1, 1)\) 方向走的影响。一共走 \(n + m - i\) 步，其中有 \(i\) 步向 \((1, 1)\) 这个方向走。贡献是：

\[\binom {n + m - i}{i} \]

两个乘起来，套上求和，就得到最终答案了。最终答案是：

\[\sum _{i \le m} \left(\binom{n + m - 2i}{m - i} - \binom{n + m - 2i}{m - i - 1}\right) \binom {n + m - i}{i} \]

预处理阶乘和逆元后直接算就行了。时间复杂度 \(O(T\sqrt n)\)。

#include<iostream>
#include<fstream>
#include<algorithm>
#define int long long
using namespace std;
namespace azus{
	int q;
	const int P = 998244353;
	int jc[2000005], inv[2000005];
	int Ksm(int u, int v){
		int ret = 1;
		while(v){
			if(v & 1) ret = 1ll * ret * u % P;
			u = 1ll * u * u % P, v >>= 1;
		}
		return ret;
	}
	int binom(int u, int v){
		return (jc[u] * inv[v] % P) * inv[u - v] % P;
	}
	int n, m;
	int turn(int u){
		for(int i = 1; i <= 1000000; i ++){
			int l = i * (i - 1) / 2 + 1;
			int r = i * (i + 1) / 2;
			if(u >= l && u <= r){
				n = i, m = u - l + 1;
				n --, m --;
				return 0;
			}
		}
		return 0;
	}
	int main(){
		jc[0] = inv[0] = 1;
		for(int i = 1; i <= 2000000; i ++)
			jc[i] = jc[i - 1] * i % P;
		inv[2000000] = Ksm(jc[2000000], P - 2);
		for(int i = 1999999; i >= 1; i --)
			inv[i] = inv[i + 1] * (i + 1) % P;
		cin >> q;
		while(q --){
			int x; cin >> x;
			turn(x);
			int ans = 0;
			for(int i = 0; i <= m; i ++){
				int c1 = binom(n + m - 2 * i, m - i);
				int c2 = binom(n + m - 2 * i, m - i - 1);
				int c3 = binom(n + m - i, i);
				int c4 = (P + c1 - c2) % P;
				ans += (c4 * c3) % P;
				ans %= P;
			}
			cout << ans << "\n";
		}
		return 0;
	}
}
signed main(){
//	ios::sync_with_stdio(0);
//	cin.tie(0), cout.tie(0);
	int T = 1;
	while(T --) azus::main();
	return 0;
}