置换群 / Polya 原理 / Burnside 引理 学习笔记
置换群 / Polya 原理 / Burnside 引理 学习笔记
在 GJOI 上做手链强化,经过长达三小时的 OEIS 和手推无果后开摆,喜提 rnk12,故开始学习置换群相关内容。
笔记主要以 Polya 原理和 Burnside 引理的应用为主,所以会非常简单,很大一部分的群论概念和证明不会写,因为我不会。
基础群论
定义
群论主要研究的是一种叫「群」的代数结构。
群,简单来说是一个集合和一种二元运算构成的二元组 \((G, \cdot)\),并且满足群公理。
群公理:
- 二元运算 \(\cdot\) 要对集合 \(G\) 封闭。
- 满足结合律,即对于元素 \(a, b, c \in G\),要满足 \((a \cdot b) \cdot c = a \cdot (b \cdot c)\)。
- 有单位元,即存在一个元素 \(e\) 满足对于任意 \(a \in G\) 都有 \(e \cdot a = a \cdot e = a\) 成立。这个元素 \(e\) 被称为「单位元」。
- 任意一个元素都有逆元。即对于任意 \(a \in G\),一定能找到一个元素 \(a ^ {-1}\) 满足 \(a \cdot a ^ {-1} = e\),我们称 \(a\) 和 \(a ^ {-1}\) 互为单位元。
子群
对于两个群 \((G, \cdot), (H, \cdot)\),如果 \(H \subseteq G\) 并且这俩群的 \(\cdot\) 指的是同一个二元运算,那么我们称 \((H, \cdot)\) 是 \((G, \cdot)\) 的一个子群。
阶
群的阶指的是群的集合的元素个数,记作 \(|G|\)。
没了。只是学习利用置换群计数且不管证明的话,只知道这些概念够了。
置换群
置换群是一类被系统研究过的群。
置换的概念
置换是从一个 \(1\) 到 \(n\) 的排列到另一个 \(1\) 到 \(n\) 排列的映射。
例如像这样:
这个置换会将原排列的 \(1\) 用 \(4\) 代替,\(2\) 用 \(1\) 代替,\(4\) 用 \(2\) 代替。
例如这个置换接收了一个排列 \((3, 1, 2, 4)\),那么它会将其映射到排列 \((3, 4, 1, 2)\)。
置换群
置换群 \((G, \cdot)\) 中的元素为所有 \(1\) 到 \(n\) 的排列的置换。
两个置换进行 \(\cdot\) 运算可以理解为将这两个置换进行合成。
若 \(a \cdot b = c\),那么我们对任意一个排列 \(x\) 进行一次 \(a\) 置换变成 \(a(x)\),然后再对其进行 \(b\) 置换得到 \(b(a(x))\),得到的结果等于直接对原排列进行 \(c\) 置换 \(c(x)\)。也就是 \(c(x) = b(a(x))\)。
举个例子吧,假设 \(a\) 置换是 \(\large\binom{1, 2, 3, 4}{4, 1, 3, 2}\), \(b\) 置换是 \(\large\binom{1, 2, 3, 4}{4, 3, 2, 1}\)
那么有:
来验证这个群满足群公理。
- 一个置换进行 \(\cdot\) 运算后还是一个置换,显然满足封闭性。
- 试一下就知道结合律是满足的。
- 有单位元,单位元是 \(\large\binom{1, 2, 3, 4}{1, 2, 3, 4}\)。
- 有逆元,交换上下两行即可。
所以这玩意是满足的。
Burnside 引理
设 \(A, B\) 是两个有限集合,\(X\) 是一些 \(A\) 到 \(B\) 的映射的集合。
\(G\) 是 \(A\) 上的置换群,\(X\) 的映射在 \(G\) 的作用下封闭。
\(X / G\) 是 \(G\) 作用在 \(X\) 上的所有等价类的集合。
(如果 \(X\) 中的两个映射经过 \(G\) 的置换后相等,那么这俩映射就在一个等价类中)
那么有:
其中 \(|S|\) 是指集合 \(S\) 的元素个数。\(X^g\) 定义如下。
如果有点难懂的话那就举个例子吧。
(因为 OI Wiki 上的正方体的例子需要思考()所以搬了另一个例子过来)
(出自 集训队论文 符文杰:《Pólya原理及其应用》)
一个简单的例子:
将一个 \(2 \times 2\) 的矩阵黑白染色,问有多少种本质不同的方案?如果两个矩阵可以通过旋转相互吻合,那么算同一种方案。
首先先列出来吧。
不考虑本质不同,一共有 \(16\) 种方案:
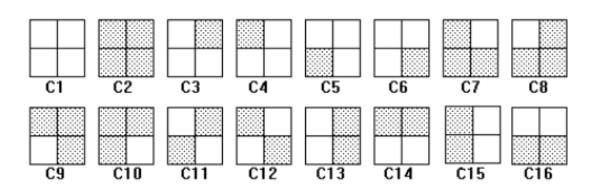
其中本质不同的有 \(6\) 种,其他方案都可以由下面的方案旋转得到。
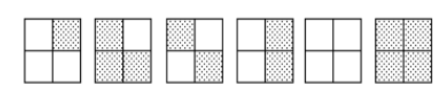
把上面的集合列出来吧。
\(A\):表示四个格子的集合。
\(B\):表示黑白两种颜色的集合。
\(X\):不考虑本质不同,直接在四个格子上染色的方案的集合。每个格子可染可不染,总共有 \(2 ^ 4 = 16\) 种方案。
\(G\):所有旋转操作构成的置换群。集合中有四个元素,分别是:转 \(0 ^{\circ}\),转 \(90 ^{\circ}\),转 \(180 ^{\circ}\),转 \(270 ^{\circ}\)。(本文内旋转默认顺时针)
\(H / G\):本质不同的染色方案的集合。
套公式吧,下面来探究 \(G\) 中每个元素 \(X^g\) 是什么。下面分别称四个格子(左上,右上,左下,右下)为 \(1, 2, 3, 4\) 格子。
- 转 \(90 ^{\circ}\)。也就是 \((1, 2, 3, 4)\) 置换为 \((2, 3, 4, 1)\)。要求 \((1, 2), (2, 3), (3, 4),(4, 1)\) 格子颜色一样,也就是所有格子颜色一样,所以一共有 \(2\) 种方案,也就是图中的 C1 和 C2。
- 转 \(180 ^{\circ}\)。也就是 \((1, 2, 3, 4)\) 置换为 \((3, 4, 1, 2)\)。要求 \((1, 3), (2, 4)\) 格子颜色一样。对于每组格子都能选择两种颜色,所以一共有 \(4\) 种方案,也就是图中的 C1,C2,C11,C12。
- 转 \(270^{\circ}\)。也就是 \((1, 2, 3, 4)\) 置换成 \((4, 1, 2, 3)\)。和第一种情况一样,一共有 \(2\) 种方案,C1 和 C2。
- 转 \(0^{\circ}\)。所有方案都满足,所以有 \(16\) 种。
所以根据公式:
然后我们就得到了本质不同的方案有 \(6\) 种。
这里问题规模较小所以可以枚举解决,但是问题规模增大到 \(20 \times 20\) 甚至 \(200 \times 200\) 的时候靠枚举可就很难解决了。
证明不会。反正 OI 不考证明()
Polya 原理
数有多少个点置换后不动是不是很烦?那么还有更简单的式子。
定义与 Burnside 引理的定义相同。
如果 \(X\) 是 \(A\) 到 \(B\) 所有的映射,那么有:
其中 \(c(g)\) 表示对于元素 \(g\),它能拆成多少个子置换。
举个例子,例如置换
我们能把它拆成三个子置换:
所以 \(c(g) = 3\)。
这就是 Polya 原理。
上面的例题太简单了,让我们把规模增长到 \(3 \times 3\)。
因为所有的染色方案都是允许的,没有说什么某个格子不能涂黑啊、哪个格子不能涂白啊,所以满足 Polya 原理的前置条件。
讨论每个置换的 \(c(g)\)。为了简便,下面不写置换第一行的 \((1, 2,3, 4, \dots, 9)\)
- 转 \(0 ^{\circ}\):置换为 \((1, 2, 3, 4, 5, 6, 7, 8, 9)\),共有 \(9\) 个子置换,\(c(g) = 9\)。
- 转 \(90 ^{\circ}\):置换为 \((3, 6, 9, 2, 5, 8, 1, 4, 7)\),共有 \(3\) 个子置换,分别是 \((1, 3, 7, 9)\) 组成的子置换、\((2, 4, 6, 8)\) 组成的子置换和 \((5)\) 组成的子置换。\(c(g) = 3\)。
- 转 \(180 ^{\circ}\):置换为 \((9, 8, 7, 6, 5, 4, 3, 2, 1)\),共有 \(5\) 个子置换,除了 \(5\) 以外其他数字都能两两分组组成一个子置换。\(c(g) = 5\)。
- 转 \(270 ^{\circ}\):置换为 \((7, 4, 1, 8, 5, 2, 9, 6, 3)\),共有 \(3\) 个子置换,看到自己想必大家都能自己数出来了。\(c(g) = 3\)。
套公式吧。
所以有 \(140\) 种本质不同的染色方案。
感兴趣的读者自己验证吧反正我懒了。
如果你枚举法,那么枚举 \(512\) 种方案非常复杂。即使使用 Burnside 引理,求不动点也就是 \(|X^g|\) 也是很复杂的,这个时候就体现出 Polya 原理的优势了。
例题
P4980 【模板】Polya 定理
给定一个 \(n\) 个点,\(n\) 条边的环,有 \(n\) 种颜色,给每个顶点染色,问有多少种本质不同的染色方案,答案对 \(10^9+7\) 取模
注意本题的本质不同,定义为:只需要不能通过旋转与别的染色方案相同。
板子题。
置换群中的置换有 \(n\) 种,分别为转 \(1\) 格至转 \(n\) 格。
考虑每种置换的 \(c(g)\)。
容易得到,对于转 \(i\) 格而言,\(c(g) = \gcd(i, n)\)。
代入公式中。
这里 \(\varphi\) 函数直接 \(O(\sqrt n)\) 算就行。
时间复杂度 \(O(n ^ {\frac 34} + \sqrt n \log n)\)
P2561 [AHOI2002] 黑白瓷砖
题面是图片所以就自己看吧。
这题也很板。
操作也就只有 \(6\) 种,分别是不变、旋转 \(120 ^{\circ}\)、旋转 \(240 ^ {\circ}\) 以及三个方向的翻转。
因为先翻转后旋转或者先旋转后翻转已经包括在上面的情况之中了。
图形很对称,所以只用考虑不变、旋转 \(120 ^ {\circ}\) 和一个方向的翻转,其他的是一样的。
不变的话有 \(\frac{n(n + 1)}2\) 个子置换。
考虑旋转的情况。画下图,发现所有格子三三匹配构成子置换,或者除了最中间的格子单独构成置换其他三三匹配构成子置换。所以:
- 如果 \(\frac{n (n + 1)}2\) 是三的倍数,那么 \(c(g)\) 就是 \(\frac{n (n + 1)}6\)。
- 否则中间一个点构成子置换,\(c(g)\) 是 \(\frac{n(n + 1) + 2}6\)
所以对于旋转 \(120 ^ {\circ}\) 和旋转 \(240 ^ {\circ}\),其 \(c(g)\) 的值见上方所示。
考虑翻转的情况。画下图,发现中轴线上穿过的格子翻转后不变,其他格子两两匹配构成子置换。
有 \(\left\lceil \frac n2 \right\rceil\) 个格子被中轴线穿过,所以这时候 \(c(g) = \frac{\frac {n(n + 1)}2 + \left\lceil \frac n2 \right\rceil}2\)。
然后套公式就行了。
这题要高精度所以我没写代码。
GJOI 2024/2/15 T2 手链强化
要给一个 \(n\) 个节点的环染色,每个点可以染成 \(k\) 种颜色的一种或者不染色。环上相邻的点不能同时染色。求本质不同方案数。
\(n, m \le 10^9\)
不满足 Polya 原理的前置条件,所以考虑 Burnside 引理。
设 \(f(n)\) 表示 \(n\) 个点的环上不考虑旋转同构满足染色节点不相邻的方案数。
先用 Burnside 引理推下式子。
考虑怎么计算 \(f(n)\)。
很容易想到一个 \(O(n)\) 的 dp。
设 \(f_{i, 0/1}\) 表示考虑前 \(i\) 个点,当前点染色或不染色的方案数。
容易得到状态转移方程:
因为是环,首尾相接而首尾不能同时染色,所以要做两次 dp,第一次钦定第一位不染色,第二次钦定最后一位不染色即可。
但是这样时间复杂度还是很高。
其实这个 dp 方程是简单的递推,矩阵优化即可。
时间复杂度 \(O(n ^ {\frac 34} + \sqrt{n} \log n)\)。
[MtOI2018] 魔力环
要求给一个 \(n\) 个节点的环染上 \(m\) 个黑色节点和 \(n - m\) 个白色节点,并且满足环上不包含一段连续的长度超过 \(k\) 的黑色节点。求本质不同方案数。
\(n, k \le 10 ^ 5\)
一样的。设 \(f(x)\) 表示 \(x\) 个点的环上不考虑旋转同构满足不包含一段连续的长度为 \(k\) 的节点的方案数。
如果我们知道了 \(x\),那么我们能推出在这个环上黑色点和白色点的数量。具体而言,因为对于一个长度为 \(x\) 的等价类,它会在大环中重复 \(\frac nx\) 次,所以会有 \(\frac {mx} n\) 个黑色节点和 \(\frac {(n - m) x }n\) 个白色节点。
那么设 \(S(n, m)\) 表示 \(n\) 个节点其中有 \(m\) 个黑色节点,不考虑旋转同构满足不包含一段连续的长度为 \(k\) 的节点的方案数。
固定白色节点,在白色节点的间隙中插入黑色节点。
因为在一个环上,所以第一个间隙和最后一个间隙本质是相同的,所以第一个间隙和最后一个间隙的黑色珠子数量的和不能超过 \(k\)。
枚举放在第一个间隙和最后一个间隙的黑色珠子数量,然后就能转化为序列上的问题了。
假设第一个间隙和最后一个间隙的黑色珠子数量和为 \(i\),那么问题就转换成了:
在 \(n - m - 1\) 个白色珠子的间隙中插入 \(m - i\) 个黑色珠子,每个间隙中不可以有超过 \(k\) 个黑色珠子,求方案数。
转换为球和盒子的问题,即在 \(n - m - 1\) 个有标号盒子中放入 \(m - i\) 个无标号球,盒子容量上限为 \(k\),求方案数。
设 \(R(n, m)\) 表示 \(n\) 个有标号格子中放入 \(m\) 个无标号球,盒子的容量上限是 \(k\) 的方案数。
容斥一下。枚举有至少 \(i\) 个盒子容量超过 \(k\)。然后问题就变成了 \(n\) 个有标号格子中放入 \(m - i(k + 1)\) 个小球的方案数。这个东西组合数算一下就行了,很简单。
然后套 Burnside 引理的式子就行了。
P1446 [HNOI2008] Cards
给定一个置换群 \(G\)。
问将 \(n\) 张牌染成 \(S_r\) 张红色 \(S_b\) 张蓝色 \(S_g\) 张绿色形成的集合经过置换群 \(G\) 的作用后形成的等价类数量。
\(m = |G| \le 60, \max{S_r, S_g, S_b} \le 20\)
Burnside 引理。
对于一个置换,一种染色方案在这个置换作用下相等,相当于要求这一置换的所有子置换内部染的颜色相同。
假设置换 \(g\) 能拆分成 \(k\) 个子置换,长度分别为 \(l_1, l_2, \dots, l_k\)。
那么我们要算将 \(l\) 数组划分为三个集合的方案,使得这三个集合内部的 \(l_i\) 之和分别为 \(S_r, S_g, S_b\) 的方案数。
这里可以用背包 dp,但是我做题的时候没想到所以用的是搜索。
设 \(cnt_i\) 表示有多少个 \(j\) 满足 \(l_j = i\),\(cntr_i\) 表示有多少个长度为 \(i\) 的置换被染成了红色,\(cntg_i\) 和 \(cntb_i\) 同理。
我们可以直接通过搜索划分 \(S_r\) 和 \(S_g\),枚举所有可能的 \(cntr_i\) 和 \(cntg_i\)。
然后就有 \(cntb_i = cnt_i - cntr_i - cntg_i\)。
那么根据多重排列数,当前 \(cntr\) 和 \(cntg\) 的贡献为 \(\large\prod_{i = 1} ^ n\frac {cnt_i!}{cntr_i!cntg_i!cntb_i!}\)
所以对于置换 \(g\),有:
这个暴力算就行。因为 \(\operatorname{Partitions}(20)\) 在 \(800\) 左右的。
最后带入到 Burnside 引理中即可。
时间复杂度 \(O(nm\operatorname{Partitions} ^ 2(\max(S_r, S_b, S_g)))\)
看似很大过不了,但是完全跑不满,所以完全能过,而且跑得挺快的。
P4128 [SHOI2006] 有色图
用 \(m\) 种颜色将一个顶点数为 \(n\) 的无向完全图的边染色,如果两张图能通过一种将顶点重新标号的方案变为相同则称这两张图本质相同。求本质不同的染色方案数。
\(n \le 53, m \le 1000\)
“什么?有色图?哪里有色图?”
这题的置换是作用在顶点上的,但是这题的染色是在边上的,所以我们需要找到点的置换和边的关系。
假设一个置换 \(g\) 能拆成 \(k\) 个长度为 \(l_1, l_2, \dots, l_k\) 的子置换,套路地讨论 \(X^g\) 的计算方法。
先考虑子置换内的情况。
考虑子置换 \(g_1\),假设其为 \((p_1, p_2, p_3, \dots, p_{l_1})\)
其内部连成的边为 \((p_1, p_2), (p_2, p_3), (p_1, p_3), \dots\)
当我们执行一次置换,排列变成了 \((p_2, p_3, p_4, \dots, p_{l_1}, p_1)\),边变成了 \((p_2, p_3), (p_3, p_4), (p_2, p_4), \dots\)
设 \(c(i, j)\) 表示边 \((i, j)\) 的颜色。
因为我们要让置换后前后不变,所以要满足 \(c(p_1, p_2) = c(p_2, p_3), c(p_1, p_3) = c(p_2, p_4), \dots\)
也就是所有在子置换中距离相同的点形成的边颜色要相同。
形象地,如果我们将 \(p\) 中的点等距的放在一个园上,然后按原完全图进行连边,那么边长相同的边颜色要相同。
边长相同的边有 \(\left\lceil\frac l2\right\rceil\) 组,所以置换内的贡献为 \(\sum _{i = 1} ^ k \left\lceil\frac {l_i}2\right\rceil\)。
然后考虑两个子置换之间的情况。
举个例子吧,假设有两个子置换,其长度分别为 \(2\) 和 \(6\),分别称这两个子置换为 \(a, b\)。
那么,边 \((a_1, b_1)\) 经过置换变为 \((a_2, b_2)\),然后变为 \((a_1, b_3)\),\((a_2, b_4)\),\((a_1, b_5)\),\((a_2, b_6)\),\((a_1, b_1)\)。
上面的边组成一个等价类,其他的边组成一个等价类,共两个。
再举一些例子就能得到对于两个长度为 \(l_i, l_j\) 的子置换,贡献等价类数量为 \(\gcd(i, j)\)。
所以一个置换构成的等价类数量为 \(\sum _{i = 1} ^ k \left\lceil\frac {l_i}2\right\rceil + \sum_{i = 1}^{k} \sum_{j = 1}^k \gcd(l_i, l_j)\)。
所以
回到 burnside 引理的式子:
这明显还是算不了一点的样子嘛!
细看,发现一个置换的 \(|X ^ g|\) 只与其 \(l\) 数组有关。也就是我们可以反过来,枚举 \(l\) 数组,也就是像上题那样枚举 \(n\) 的划分,并且统计有多少个置换的 \(l\) 数组是这样子的。
首先是一个多重排列,把 \(n\) 个数塞到 \(k\) 个子置换里,贡献是:
在每个子置换里分配数的顺序,这相当于一个圆排列,又要乘上一个 \(\prod _{i = 1}^{k} (l_i - 1) !\)。
但是这样会算重,和上题一样,如果有相等的 \(l_i\) 就会出现重复,所以还需要除以 \(\prod_{i = 1} ^{n} cnt_i!\)。
综合起来就是
这里的 \(n!\) 可以和前面的 \(\frac1{n!}\) 约掉。
dfs 即可。实现的比较好的话 \(m\) 的指数是可以在 dfs 过程中算出来的。
时间复杂度是 \(O(\operatorname{Partitions}(n))\)
P4727 [HNOI2009] 图的同构计数
求 \(n\) 个点的本质不同的简单图的个数。两张图本质相同指的是有一种给图中的点重新编号的方案使得这两张图完全一样。
\(n \le 60\)
这题和上题本质相同,所以要除掉(误
维护本质不同的简单图,本质是维护在点置换后一些边是否存在。
考虑回到上题,如果把边存在当作染成黑色,边不存在当作染成白色,那就变成了这题。
所以这题就是上题 \(m = 2\) 的情况,秒了(
[ABC284Ex] Count Unlabeled Graphs
给定整数 \(n\),\(k\) 和质数 \(P\)。
你需要在一个 \(n\) 个节点的无标号无向图上给每一个节点标上一个 \(1\) 到 \(k\) 的数,且每一个数都要用到,求出标号后本质不同的图的数量对 \(P\) 取模。
\(1 \le k \le n \le 30\)
这题在上题的基础上多了一个顶点上要有标号。
容易发现顶点上的标号和边的有无是没有关系的,所以只需要在上题的基础上乘上点标号的方案数就行了。
\(n\) 和 \(k\) 都很小,所以直接 dp。我们要求的相当于 \(n\) 个有标号球放入 \(m\) 个有标号盒子,每个盒子里至少有一个球的方案数。
设 \(f_{i, j}\) 表示 \(i\) 个有标号球放入 \(j\) 个有标号盒子的方案数。
考虑第 \(i\) 个球放哪里。如果前 \(i - 1\) 个球已经放进 \(j\) 个盒子里了,那么这个球随便放,否则这个球只能放在第 \(j\) 个盒子里。
所以有状态转移方程:
然后在算 \(|X^g|\) 的时候,因为置换后要不变,所以每个等价类的顶点都应该标有同一数字。
所以只用在算 \(|X^g|\) 的时候把 \(f\) 数组乘进去就行了。
没了。
真没了。
你问 烷烃计数 烷基计数 烯烃计数 同分异构体计数 呢?
看我什么时候学完多项式再回来填。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号