被数学爆杀了

\(~~~~\) 在做这道题的前一天晚上，笔者在一套含有大量解析几何内容数学考试中获得了92分（满分150分）的好成绩。高出班主任口中班级最高1分（？）。特记之。

题意

\(~~~~\) 给出 \(n\) 个点表示一个陆地的剖面图的顶点。可以选择两个点 \((x_1,y_1)\) 和 \((x_2,y_2)\) 向上立两根 \(h-y_1\) 和 \(h-y_2\) 的柱子，建造一个中空部分为半径 \(r=\frac{(x_2-x_1)}{2}\) 的半圆拱桥。但拱桥不允许与给出的陆地相交。定义建造总代价为 柱子高度的和 \(\times \alpha\) 加上两根相邻柱子之间跨度的平方的和 \(\times \beta\) 。求代价最小且合法方案的代价。
\(~~~~\) \(2\leq n\leq 10^4\).

题解

\(~~~~\) 不难想到暴力 \(dp\) ：记 \(dp_{i}\) 表示在第 \(i\) 个点有立柱子且前面均已造好桥的最小代价。那么枚举上一个点 \(j\) ，对于点对 \((l,r)\) 显然可得圆心 \((\dfrac{x_l+x_r}{2},h-r)\) 。只要对中间一点 \(k\) 有 \(y_k>y_o\) 然后利用距离暴力判断是否对于中间所有点其都在中空部分。

\(~~~~\) 很明显这是一个 \(\mathcal{O}(n^3)\) 的 \(dp\) ，观察数据范围可以发现大概我们需要的是 \(n^2\) 的做法，考虑怎么优化。

\(~~~~\) 很显然如果我们倒着扫做断电的话，如果我们能充分利用中间已经扫过的点那很有可能可以快速判断一个点的合法性。考虑对于中间一个点 \((x,y)\) ，右端点的横坐标为 \(x_r\) ，左端点的横坐标为 \(x_l\) ，那么：

\[(x-\frac{l+r}{2})^2+(y-h+\frac{r-l}{2})^2 ≤(\frac{r-l}{2})^2 \]

\(~~~~\) 暴力拆开化简（使用WolframeAlpha）得到下式：

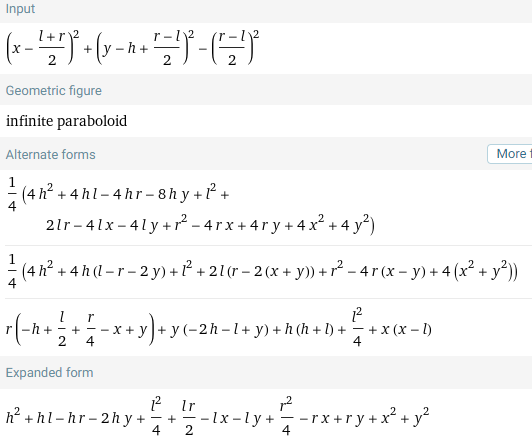
\(~~~~\) 然后手动整理一下：

\[l^2+(2r-4x-4y+4h)l+r^2+4x^2-4xr+4y^2-8yh+4yr+4h^2-4hr\leq 0 \]

\(~~~~\) （其实手化的时候我也拆到这么散，所以数学92分情有可原）

\(~~~~\) 然后就可以解得 \(l\) 的范围进行一个缩小范围。

\(~~~~\) 然后需要注意的就是当当前这个中间点 \(i\) 有 \(r< h-y_i\) 时那这个右端点不应该被更新，看一下几何关系就可以知道。

代码

#include <bits/stdc++.h>
#define ll long long
using namespace std;
template<typename T>void read(T &x)
{
    T f=1;x=0;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
    while(s>='0'&&s<='9') {x=x*10+s-'0';s=getchar();}
    x*=f;
}
int n,h,a,b;
ll dp[10005],X[10005],Y[10005];
inline ll Squ(int x){return 1ll*x*x;}
int main() {
	read(n);read(h);read(a);read(b);
	for(int i=1;i<=n;i++) read(X[i]),read(Y[i]);
	dp[1]=a*(h-Y[1]);
	for(int r=2;r<=n;r++)
	{
		dp[r]=1e18;
		double L=X[r]-2*h+2*Y[r],R=X[r];
		for(int i=r-1;i>=1;i--)
		{
			ll A=1,B=2*X[r]-4*X[i]-4*Y[i]+4*h,C=Squ(X[r])+4ll*Squ(X[i])-4ll*X[i]*X[r]+4ll*Squ(Y[i])-8ll*(Y[i]*h)+4ll*Y[i]*X[r]+4ll*Squ(h)-4ll*h*X[r];
			ll Delta=Squ(B)-4ll*A*C;
			if(Delta<0) break;
			L=max(L,1.0*(-B-sqrt(Delta))/(2ll*A));
			if(X[r]-X[i]>=2ll*(h-Y[i])) R=min(R,1.0*(-B+sqrt(Delta))/(2ll*A));
			if(L<=X[i]&&X[i]<=R&&dp[i]<=1e18) dp[r]=min(dp[r],dp[i]+1ll*a*(h-Y[r])+1ll*b*Squ(X[r]-X[i]));
		}
	}
	if(dp[n]==1e18) puts("impossible");
	else printf("%lld",dp[n]);
	return 0;
}