状压dp-其一
关于二进制
判断包含关系
如果集合A是集合B的子集,那么集合A的每一个元素都属于集合B。
那么,集合A与集合B的交集即为集合A,而它们的并集即为集合B。
用位运算描述,若(A&B)==A,则A∈B; 若(A|B) ==B,则A∈B。
在C++中,只需判断:
if( (A&B)==A ) 则集合A是集合B的子集
else 则集合A不是集合B的子集
或者在C++中判断:
if( (A|B)==B ) 则集合A是集合B的子集
else 则集合A不是集合B的子集
考虑总共有5个元素构成的全集U={5,4,3,2,1},他们表示5个学生的学号。
若知道喜欢踢足球的学生的学号对应的二进制数写成十进制数后是10,
也知道喜欢打篮球的学生的学号对应的二进制数写成十进制数后是14,
问喜欢踢足球的学生是不是喜欢打篮球的学生的子集?
根据上面的判断方法,设a=10, b=14,
if( (a&b) == a) 则喜欢踢足球的是喜欢打篮球的子集
else 则喜欢踢足球的不是喜欢打篮球的子集
全集
若要研究的问题总共有n个元素。那么全集U为{n,n-1,......2,1},全集对应的二进制数是11…1 (共n个1)。
这样一个集合的二进制对应的十进制数是多少呢? 容易得知,是, 则 (1<<n) - 1。
补集
若集合A是集合U的子集,那么A在U中的补集为U中不属于A的元素的集合。
由于A中的元素必定存在于U中,这等价于不同时存在于A和U但至少存在于其中一个集合的元素的集合,
也就二进制异或运算的结果。用位运算描述,A在U中的补集 = A^U。
差集
集合A与集合B的差集,即为属于集合A但不属于集合B的元素的集合。
也就是说,我们从集合A中去掉同时属于A和B的元素,得到的就是A与B的差集,即它们的交集在A中的补集。
用位运算描述,A-B=A^(A&B)。
例题一 原子弹(程序填空)
最近,火星研究人员发现了N个强大的原子。他们互相都不一样。
这些原子具有一些性质。当这两个原子碰撞时,其中一个原子会消失,产生大量的能量。
研究人员知道每两个原子在碰撞时的能释放的能量。
你要写一个程序,让它们碰撞之后产生最多的总能量。
【输入格式】
第一行是整数N(2 <= N <= 10),这意味着有N个原子:A1到AN。
然后下面有N行,每行有N个整数。
在第i行中的第j个整数表示当i和j碰撞之后产生的能量,并且碰撞之后j会消失。
所有整数都是正数,且不大于10000。
【分析题目】
举例分析问题 ,N=3, M数组如下
0 3 7
2 0 6
5 2 0
考虑用动态规划。
用f{3,2,1}表示原问题,则状态是一个集合。
如何找子问题?
取集合里面的两个原子弹出来碰撞, 这样会有一个原子弹消失,那么原子弹的集合就会少一个元素,从而变成了子问题。
(1)那原子弹1碰撞原子弹2,得到能量3,原子弹2消失,变成子问题: f{3,1}, 记 A = 3 + f{3,1}
(2)那原子弹1碰撞原子弹3,得到能量7,原子弹3消失,变成子问题: f{2,1}, 记 B = 7 + f{2,1}
(3)那原子弹2碰撞原子弹1,得到能量2,原子弹1消失,变成子问题: f{3,2}, 记 C = 2 + f{3,2}
(4)那原子弹2碰撞原子弹3,得到能量6,原子弹3消失,变成子问题: f{2,1}, 记 D = 6 + f{2,1}
(5)那原子弹3碰撞原子弹1,得到能量5,原子弹1消失,变成子问题: f{3,2}, 记 E = 5 + f{3,2}
(6)那原子弹3碰撞原子弹2,得到能量2,原子弹2消失,变成子问题: f{3,1}, 记 F = 2 + f{3,1}
原问题f{3,2,1} = max( A, B, C, D, E, F), 所以只有能求出ABCDEF,就能求出原问题。
下面分析如何A,其他BCDEF同理求。
A = 3 + f{3,1},只要求出子问题f{3,1}就能求出A。
如何求f{3,1}? 分两种情况:
(1)原子弹1碰撞原子弹3,得到能量7,原子弹3消失,变成子问题:f{1},易知f{1} = 0
(2)原子弹3碰撞原子弹1,得到能量5,原子弹1消失,变成子问题:f{3},易知f{3} = 0
所以 A = 3 + f{3,1} = max(7+0, 5+0) = 3 + 7 = 10。
同理可以求出:
B= 7 + f{2,1} = 7 + 3 = 10
C = 2 + f{3,2} = 2 + 6 = 8
D = 6 + f{2,1} = 6 + 3 = 9
E = 5 + f{3,2} = 5 + 6 = 11
F = 2 + f{3,1} = 2 + 7 = 9
所以原问题f{3,2,1} = max(A,B,C,D,E,F) = max(10,8,9,11,9) = 11
通过上面的分析可以发现, 子问题集合的元素个数比原问题集合的元素个数少。
所以我们计算顺序是: 先算集合元素个数少的,再算集合元素个数多的。
集合元素的个数L 集合对应的f值
L=1
f{1} = 0
f{2} = 0
f{3} = 0
L=2
f{2,1} = 3
f{3,1} = 7
f{3,2} = 6
L=3 f{3,2,1} = 11
这种计算顺序(即动态规划的阶段)虽然正确性没问题,但是比较麻烦。
因为状态是一个集合,表示起来比较麻烦, 例如 f{3,1},在C++如何表示?
f[{3,1}]?这样肯定不行(除非用f是map类型), f数组的下标希望是整型。
接下来,我们换一种计算顺序,不再是从集合元素个数从少算到多。
用新的计算顺序来计算上面的样例:
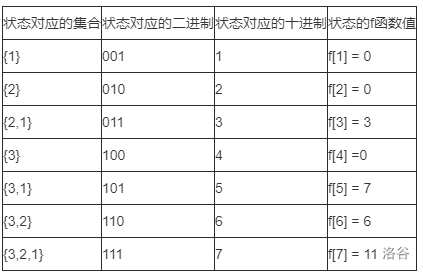
可以发现,上面的计算顺序是按照十进制数1至7所对应的集合的来计算。
这样编程就容易了:
for(int i=1; i<=7; i++) f[i] = max( ...... );
但是有一个问题,在计算f[i]时,会不会出现后效性?(动态规划要满足无后效性)
for(int i=1; i<=7; i++)
{
f[i] = ?;
因为i是从小到大的计算顺序,所以在计算f[i]时,必须保证f[i]的值只和f[0],f[1],f[2],...f[i-1]有关,
f[i]的值不能和f[i+1],f[i+2],......有关。
即f[i]无后效性。
}
幸运的是,f[i]的计算过程确实是无后效性。
下面看看计算f[7]时,是如何计算的。
首先,十进制数7表示的二进制数是111,所以111表示的集合是{3,2,1}。
求f[7]实际就是求f{3,2,1},根据前面的分析可以知道:
取集合里面的两个原子弹出来碰撞, 这样会有一个原子弹消失,那么原子弹的集合就会少一个元素,从而变成了子问题。
(1)那原子弹1碰撞原子弹2,得到能量3,原子弹2消失,变成子问题: f{3,1} = f[5], 记 A = 3 + f[5]
(2)那原子弹1碰撞原子弹3,得到能量7,原子弹3消失,变成子问题: f{2,1} = f[3], 记 B = 7 + f[3]
(3)那原子弹2碰撞原子弹1,得到能量2,原子弹1消失,变成子问题: f{3,2} = f[6], 记 C = 2 + f[6]
(4)那原子弹2碰撞原子弹3,得到能量6,原子弹3消失,变成子问题: f{2,1} = f[3], 记 D = 6 + f[3]
(5)那原子弹3碰撞原子弹1,得到能量5,原子弹1消失,变成子问题: f{3,2} = f[6] , 记 E = 5 + f[6]
(6)那原子弹3碰撞原子弹2,得到能量2,原子弹2消失,变成子问题: f{3,1} = f[5] , 记 F = 2 + f[5]
所以f[7]只与子问题f[3]、f[5]、f[6]有关。
因为 for(int i=1; i<=7; i++) f[i] = max( ...... ); 所以在计算f[7]时,f[3]、f[5]、f[6]肯定已经计算出来了。
其实很容易知道,如果f[j]是f[i]的子问题,那么j一定小于i。证明?
其实很简单,因为j是i去掉1个原子弹之后得到的集合,所以j对应的二进制数一定小于i对应的二进制数,
那么j对应的十进制数也一定小于i对应的十进制数。
所以本题的程序框架是:
int s = (1<<N) - 1; //即s是一个十进制数,s代表全集,包含N个原子弹,s={N,N-1,......,2,1},
// 集合、 二进制数、 十进制数, 三者是一一对应的关系!
for(int i=1; i<=s; i++) //按照十进制数从1至s的顺序来计算f[i]
{
第一步:把十进制数i对应的集合,所包含的原子弹分离出来并保存到临时数组A。
例如: i = 22,那么A[] = {5,3,2},则十进制数22所代表的集合包含了第2,3,5个原子弹。
可以通过枚举第j个原子弹是否属于十进制数i所表示的集合,从而产生A数组。
int tot = 0; //临时变量,表示十进制数i所表示的集合,总共包含tot个原子弹。
for(int j=N; j>=1; j--) //判断十进制数i所表示的集合是否包含第j个原子弹
{
int C = 1<<(j-1);
if( (i&C) > 0) A[++tot] = j; //说明十进制数i所表示的集合包含第j个原子弹
}
第二步: 从A数组里面任意取出两个原子弹(不妨假设是X和Y),分别用X碰撞Y,用Y碰撞X,都能变成子问题。
for(int u = 1; u < tot; u++)
for(int v = u + 1; v <= tot; v++)
{
int X = A[u];
int Y = A[v];
(1)用X碰撞Y,得到能量M[X][Y], 子问题是什么?
因为碰撞后第Y个原子弹消失,那么子问题就是从十进制数i代表的集合里面去掉第Y个原子弹,如何表示子问题的状态呢?
第Y个原子弹对应的二进制数是: 1 << (Y-1) , 不妨记为 Z = 1<<(Y-1);
根据前面所学的集合与二进制的关系,子问题的状态为: i - Z = i ^ Z, 即i异或Z
所以 f[i] = max(f[i], M[X][Y] + f[i^Z]);
(2)用Y碰撞X,得到能量M[Y][X], 子问题是什么?
因为碰撞后第X个原子弹消失,那么子问题就是从十进制数i代表的集合里面去掉第X个原子弹,如何表示子问题的状态呢?
第X个原子弹对应的二进制数是: 1 << (X-1) , 不妨记为 Z = 1<<(X-1);
根据前面所学的集合与二进制的关系,子问题的状态为: i - Z = i ^ Z, 即i异或Z
所以 f[i] = max(f[i], M[Y][X] + f[i^Z];
}
}
cout<<f[s]<<endl;
时间复杂度: O(2^n * n * n )
例题二 O - Matching
题目大意
有n本不同的书,编号1至n。
有n个不同的书包,编号1至n。
冬令营开始了,有n个学生,每个学生将会获得1个书包和1本书。
给出二维数组a[1...n][1...n],如果a[i][j]=1表示第i本书和第j个书包是兼容的,
若a[i][j]=0表示第i本书和第j个书包是不兼容的。
每个学生收到的1个书包和1本书必须是兼容的。
n本书和n个书包之间,有多少种不同的匹配方案。
1<=n<=21
做法
我们记f[i][j]为现在到第i个人,还剩下二进制集合j的书(0为可以选,1为已经被选),答案即为f[n][(1<<n)-1]
时间复杂度O(2^n * n)
实际上我们还可以发现我们可以去掉第i个人的那一维(
代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=24,p=1e9+7;
int n,x,a[maxn],f[maxn][(1<<21)+10],d[(1<<21)+10];
int check(int num){
int cnt=0;
while(num!=0){
if(num&1)cnt++;
num=num/2;
}
return cnt;
}
signed main(){
cin>>n;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
cin>>x;
if(x==1)a[i]+=(1<<(j-1));
}
}
for(int i=1;i<(1<<n);i++)d[i]=check(i);
f[0][0]=1;
for(int i=1;i<=n;i++){
for(int j=1;j<(1<<n);j++){
if(d[j]!=i)continue;
for(int k=1;k<=n;k++){
int Num=(1<<(k-1));
if((j&Num) && (a[i]&Num))f[i][j]=(f[i][j]+f[i-1][j^(j&Num)])%p;
}
}
}
cout<<f[n][(1<<n)-1];
return 0;
}
例题三 U - Grouping
题目大意
有n只兔子,编号1至n。
给出二维数组a[1...n][1...n]其中a[i][j]表示第i只兔子和第j只兔子的兼容度,
数据保证a[i][i]=0, a[i][j] = a[j][i]。
现在你需要把这n只兔子分成若干组,使得每只兔子仅属于一个组。
当分组结束后,对于1<=i<j<=n,你将会获得a[i][j]元钱,前提是第i只兔子和第j只兔子分在了同一组。
应该如何分组,才能使得最终赚的钱最多
1<=n<=16
做法
与上一题类似的,我们记f[i]为二进制集合i(1为已选,0为未选)的分配方案的最大值,对于一个状态,我们枚举他的子集,使子集内的分在一组
时间复杂度为O(3^n)
代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=16;
int n,a[maxn+5][maxn+5],f[(1<<maxn)+10],s[maxn+5],d[(1<<maxn)+10];
signed main(){
cin>>n;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
cin>>a[i][j];
f[0]=0;
for(int i=1;i<(1<<n);i++){
int len=0;
for(int j=1;j<=n;j++)
if(i&(1<<(j-1)))
s[++len]=j;
for(int j=1;j<=len;j++)
for(int k=j+1;k<=len;k++)
d[i]+=a[s[j]][s[k]];
// cout<<i<<" "<<d[i]<<endl;
for(int j=i;j!=0;j=(j-1)&i)
f[i]=max(f[i],f[i^j]+d[j]);
}
cout<<f[(1<<n)-1];
return 0;
}
例题四 开锁
题目大意
有n把锁,编号1至n。有m把钥匙,第i把钥匙的价格是p[i],第i把钥匙可以开k[i]把锁,
分别可以开第c[i][1],c[i][2],...第c[k[i]]把锁。
问你如果购买钥匙,用最少的费用把n把锁全部打开。
如果无论无何也不能把n把锁全部打开,输出-1。
1<=n<=12
做法
显然
代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=12;
int n,m,f[(1<<maxn)+10],p,N,x;
int main(){
cin>>n>>m;
memset(f,0x3f,sizeof f);
f[0]=0;
for(int i=1;i<=m;i++){
cin>>p>>N;
int Num=0;
for(int j=1;j<=N;j++){
cin>>x;
Num+=(1<<(x-1));
}
for(int j=0;j<(1<<n);j++){
f[j|Num]=min(f[j|Num],f[j]+p);
}
}
if(f[(1<<n)-1]==1061109567)cout<<-1;
else cout<<f[(1<<n)-1];
return 0;
}
例题五 旅行商
题目大意
有三维立体空间里,有n个城市,第i个城市的坐标是(x[i],y[i],z[i])。
从第i个城市到第j个城市的距离dis[i][j] = abs(x[j]-x[i]) + abs(y[j]-y[i]) + max(0,z[j]-z[i]),其中abs是求绝对值。
你需要从1号城市出发,遍历每一个城市至少一次,最后回到1号城市,问最少的旅行距离。
2<=n<=17
做法
我们记f[i][j]为二进制集合为i(1为已去,0为未去),最后到j的最短距离
时间复杂度为O(2^n * n^2)
代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=17;
int n,f[(1<<maxn)+10][maxn+5];
int d[maxn+5][maxn+5];
struct node{
int x,y,z;
}a[maxn+5];
int main(){
cin>>n;
memset(f,0x3f,sizeof f);
for(int i=1;i<=n;i++){
cin>>a[i].x>>a[i].y>>a[i].z;
}
f[1][1]=0;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(i==j)continue;
d[i][j]=abs(a[j].x-a[i].x)+abs(a[j].y-a[i].y)+max(0,a[j].z-a[i].z);
}
}
for(int i=1;i<(1<<n);i++){
for(int j=1;j<=n;j++){
if(!(i&(1<<(j-1))))continue;
for(int k=1;k<=n;k++){
if(!(i&(1<<(k-1)))||k==j)continue;
f[i][j]=min(f[i^(1<<(j-1))][k]+d[k][j],f[i][j]);
}
}
}
int minn=1e9;
for(int i=2;i<=n;i++){
minn=min(minn,f[(1<<n)-1][i]+d[i][1]);
}
cout<<minn;
return 0;
}
例题六 不同排列
题目大意
有n个学生,学号1至n。你现在需要把这n个学生从左往右排成一行形成队伍,要满足如下所有m个条件:
第i个条件的格式是x[i],y[i],z[i],表示队伍的前x[i]学生当中,学号小于y[i]的学生不能超过z[i]人。
求满足上面所有m个条件的队伍有多少种不同的方案。
2<=n<=18
做法
我们记f[i]为二进制集合为i(1为已用,0反之)的方案数
若不符合条件,则直接令之为0
代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=18;
int n,m,s[maxn+5],f[(1<<maxn)+5],b[maxn+5];
struct node{
int x,y,z;
}a[105];
bool cmp(node x,node y){
return x.x>y.x;
};
string chang(int num){
string s(n,'0');
int i=1;
while(num!=0){
s[n-i]=char(num%2+'0');
num=num/2;
i++;
}
return s;
}
signed main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
cin>>a[i].x>>a[i].y>>a[i].z;
}
sort(a+1,a+m+1,cmp);
f[0]=1;
for(int i=1;i<(1<<n);i++){
int cnt=0;
s[0]=0;
for(int j=1;j<=n;j++){
s[j]=s[j-1];
if(i&(1<<(j-1)))cnt++,s[j]++;
}
bool flag=true;
for(int j=1;j<=m&&a[j].x>=cnt;j++){
if(s[a[j].y]>a[j].z){
flag=false;
break;
}
}
if(!flag){
f[i]=0;
continue;
}
f[i]=0;
for(int j=1;j<=n;j++){
if(i&(1<<(j-1)))f[i]+=f[i^(1<<(j-1))];
}
}
cout<<f[(1<<n)-1]<<endl;
return 0;
}
例题七 序列
题目大意
有两个序列:a[1...n]和b[1...n]。你需要把序列a变成序列b。
每次你可以对序列a进行如下两种操作之一:
1、选择一个下标i(1<=i<=n),你可以让a[i]减少1或者让a[i]增加1,本次费用为X。
2、选择一个下标i(1<=i<n),你可以交换a[i]和a[i+1]的值,本次费用为Y。
你可以进行任意多次上述操作,求最少的费用使得a变成b一样。
2<=n<=18
做法
从后往前考虑,我们记f[i][j]为匹配到第i个数,还有集合j(0为可用,1不可用)可以选(这里的第一维似乎也可以省略),我们从集合j中选一个数使之与i匹配
时间复杂度为O(2^n * n)
代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=18;
int n,X,Y,f[maxn+5][(1<<maxn)+10],a[maxn+5],b[maxn+5],d[(1<<maxn)+18];
int check(int num,bool flag){
int ans=0;
string s(n,'0');
int i=-1;
while(num!=0){
ans+=num%2;
if(flag)s[++i]=char(num%2+'0');
num/=2;
}
if(flag){
cout<<s<<endl;
return -1;
}
return ans;
}
signed main(){
cin>>n>>X>>Y;
memset(f,0x3f,sizeof f);
f[n+1][0]=0;
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=n;i++)cin>>b[i];
for(int i=1;i<(1<<n);i++)d[i]=check(i,false);
for(int i=n;i>=1;i--){
for(int j=1;j<(1<<n);j++){
if(d[j]!=n-i+1)continue;
int cnt=1;
for(int k=1;k<=n;k++){
if(j&(1<<(k-1))){
f[i][j]=min(f[i][j],f[i+1][j^(1<<(k-1))]+abs(cnt-i)*Y+abs(b[i]-a[k])*X);
}
else cnt++;
}
// cout<<i<<" "<<check(j,true)<<" "<<f[i][j]<<endl;
}
}
cout<<f[1][(1<<n)-1];
return 0;
}
例题九 接龙
题目大意
有n个字符串,第i个字符串是S[i]。每个字符串都是由不超过10个小写英文字母构成。
现在A和B两人要玩字符串接龙游戏,A是先手。
每次当前玩家从剩下的字符串当中选中一个拿出来(不妨假设选中的是S[j]),
接龙到前面的字符串(不妨假设上一个被选出来的字符串是s[i]),
那么S[j]的首字母必须等于S[i]的末尾字母,这样才算接龙接得上。
如果轮到当前玩家了,而当前玩家却发现从剩下得字符串当中找不到能接得上龙得字符串,那么游戏结束,当前玩家输。
假设A和B都用最优策略玩游戏。
如果A能胜利输出"First",如果B能勝利輸出"Second"。
1<=n<=16
做法
显而易见,不写了(
代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=16;
int n;
struct node{
int fir,en;
}a[maxn+10];
string s;
int f[30][(1<<maxn)+10];
string change(int num){
string s(n,'0');
int i=-1;
while(num!=0){
s[++i]=num%2+'0';
num=num/2;
}
return s;
}
int check(bool whi,int num,int last){
if(f[last][num]!=-1)return f[last][num];
bool flag=false;
for(int i=1;i<=n;i++)
if(!(num&(1<<(i-1)))&&(last==0||last==a[i].fir))flag=flag|( whi^(check(!whi,num^(1<<(i-1)),a[i].en)));
if(flag)f[last][num]=(1^whi);
else f[last][num]=(0^whi);
// cout<<whi<<" "<<change(num)<<" "<<char(last-1+'a')<<" ";cout<<(whi^f[last][num])<<endl;
return f[last][num];
}
int main(){
memset(f,-1,sizeof f);
cin>>n;
for(int i=1;i<=n;i++){
cin>>s;
a[i].fir=s[0]-'a'+1;
a[i].en=s[s.size()-1]-'a'+1;
}
if(check(false,0,0)==1)cout<<"First\n";
else cout<<"Second\n";
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号