树状数组(Binary indexed tree)
原理
我们想要快速求数组中下标为 x ~ y 的数的和,大家第一时间都会想到用前缀和,时间复杂度为O(1)
但如果说要在线对数组进行修改的话,那用修改前缀和数组就会用O(n)的复杂度,对于q次询问,时间复杂度为O(qn),速度极不理想
这是我们就可以使用树状数组来维护
树状数组支持单点修改,单点查询,区间修改,区间查询等操作
首先我们要知道:
树状数组有一个很关键的东西,叫做lowbit,
lowbit是将一个二进制数的所有高位一都去掉,只留下最低位的1,
比如lowbit(5)=lowbit(0101(二进制))=0001(二进制)
我们看看树状数组对应的位置及其lowbit
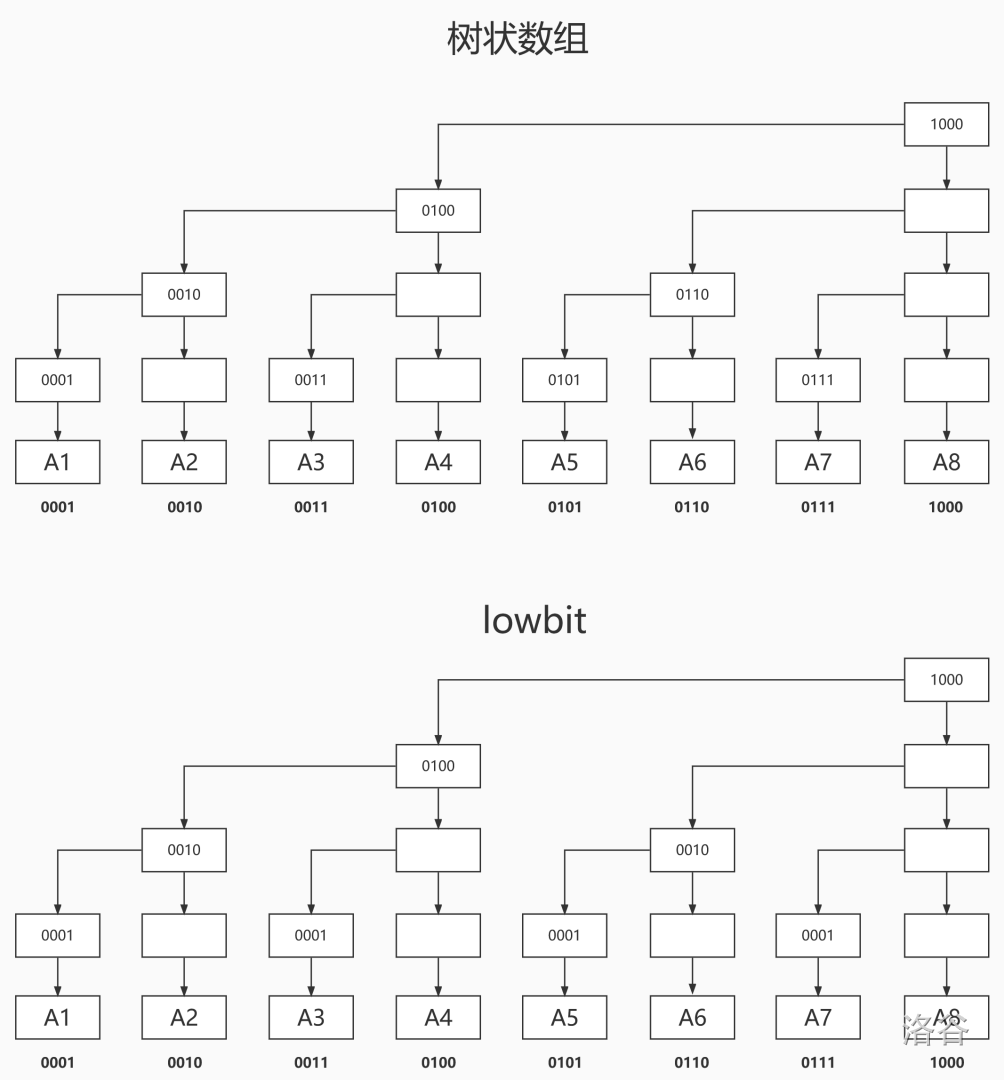
我们会发现,树状数组上的8号位(1000),它的lowbit值为8(1000),管辖着A[ 1 ~ 8 ]的节点
而树状数组上的6号位(0110),它的lowbit值为2(0010),管辖着A[ 5 ~ 6 ]的节点
树状数组上的3号位(0011),它的lowbit值为1(0001),管辖着A[ 3 ~ 3 ]的节点
......
可以猜想,树状数组上的k号位,它的lowbit值为lowbit(k),将会管辖着A[ k-lowbit(k)+1 ~ k ]的节点
所以说,要实现求 1 ~ k 的和,我们可以变为计算A[1 ~ k - lowbit(k) ]与A[ k - lowbit(k) + 1 ~ k]的和
而求A[1 ~ k - lowbit(k) ]的和也是如此,递归下去就可以得到结果
时间复杂度为O(logn)
单点修改+区间查询
那如何进行单点修改呢?
我们若对A2进行修改,如图,树状数组中2(0010),4(0100),8(1000)号位都会被修改
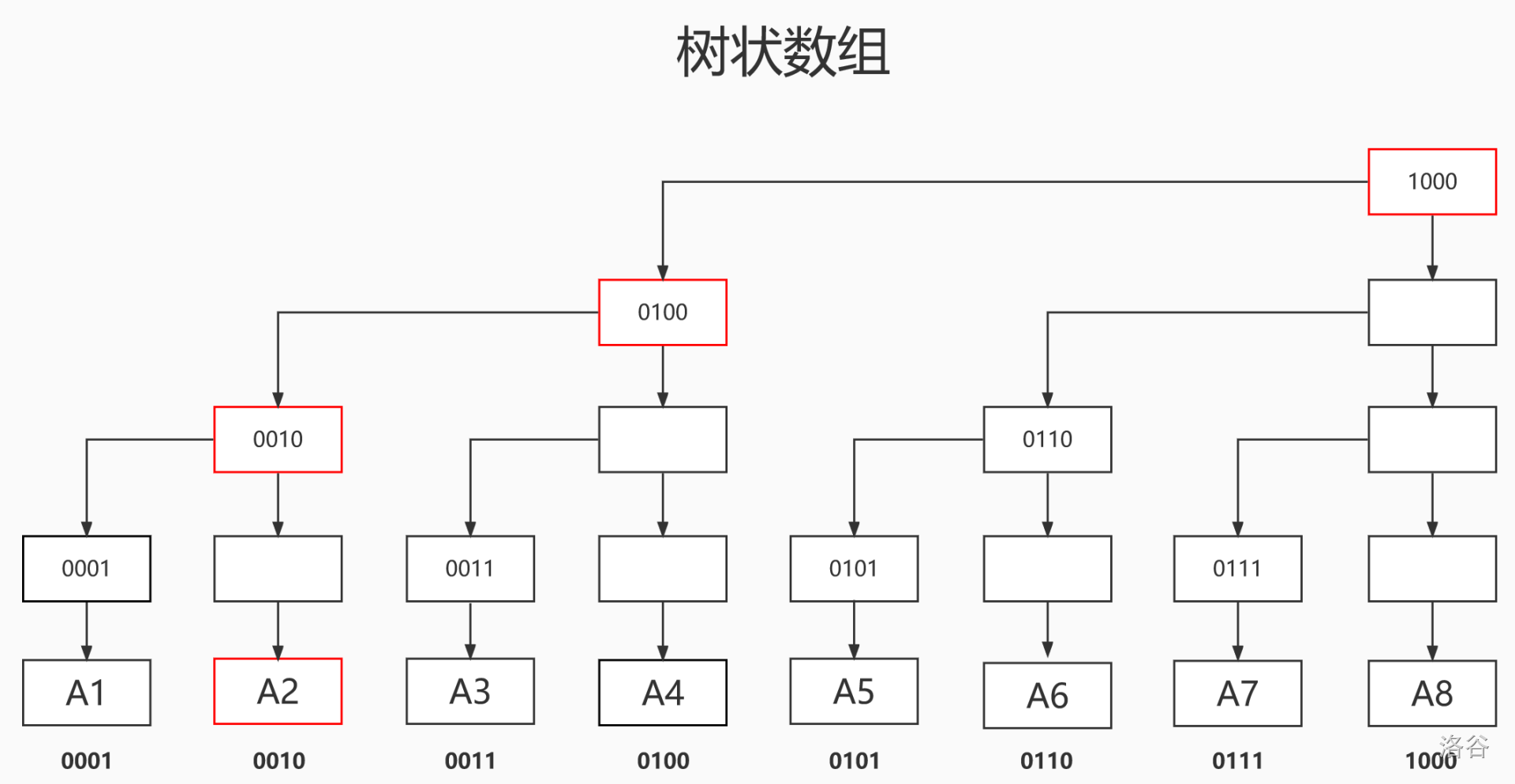
若对A5进行修改,如图,会对5(0101),6(0110),8(1000)号位造成影响

我们发现,当k号位被修改时,k + lowbit(k) 号位也会被修改,如此递归,到不能修改为止
时间复杂度为O(logn)
所以,对于q次询问,树状数组的时间复杂度只用O(qlogn)
说了那么多,那lowbit该如何实现呢?
这是,前人的智慧就凸显出来了:
lowbit(x)= x & (-x)
上代码:
#include<bits/stdc++.h>
using namespace std;
const int maxn=5*1e5+5;
int n,m,q,x,y;
struct node{
node(){
memset(a,0,sizeof a);
}
int a[maxn];
int sum(int x){
int ans=0;
for(;x;x-=x&(-x))ans+=a[x];
return ans;
}
void update(int x,int c){
for(;x<=n;x+=x&(-x))a[x]+=c;
}
}T;
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>x;
T.update(i,x);
}
while(m--){
cin>>q>>x>>y;
if(q==1)T.update(x,y);
else cout<<T.sum(y)-T.sum(x-1)<<endl;
}
return 0;
}
单点修改,查询1-n的最大值
struct Fenwick_tree{
int a[maxn+5],tr[maxn+5];
void update(int now,int c){
now++;
a[now]=c;
while(now<=K){
tr[now]=a[now];
for(int i=1;i<(now&(-now));i=(i<<1)){
tr[now]=max(tr[now],tr[now-i]);
}
now+=now&(-now);
}
}
int check(int now){
now++;
return tr[now];
}
}T;
区间修改 + 单点查询
通过“差分”(就是记录数组中每个元素与前一个元素的差),可以把这个问题转化为问题1。
查询
\(设原数组为a[i], 设数组d[i]=a[i]−a[i−1](a[0]=0),则 a[i] = \sum_{j = 1}^{i}d[j],可以通过求d[i]的前缀和查询。\)
修改
\(当给区间[l,r]加上x的时候,a[l] 与前一个元素 a[l−1] 的差增加了x,a[r+1] 与a[r] 的差减少了x。\)
\(根据d[i]数组的定义,只需给d[l] 加上 x, 给d[r+1] 减去 x 即可。\)
区间修改 + 区间查询
这是最常用的部分,也是用线段树写着最麻烦的部分——但是现在我们有了树状数组!
怎么求呢?我们基于问题2的“差分”思路,考虑一下如何在问题2构建的树状数组中求前缀和:
位置p的前缀和 =
在等式最右侧的式子\(\sum_{i = 1}^{p} \sum_{j = 1}^{i} d[j]\)中,$d[1] \(被用了\)p\(次,\)d[2]\(被用了\)p−1$次……那么我们可以写出:
位置p的前缀和 =
那么我们可以维护两个数组的前缀和:
一个数组是 \(sum1[i]=d[i]\),
另一个数组是 \(sum2[i]=d[i]∗i\)。
查询
位置p的前缀和即:$ (p + 1) * sum1\(数组中\)p$的前缀和 - \(sum2\)数组中\(p\)的前缀和。
区间\([l, r]\)的和即:位置\(r\)的前缀和 - 位置\(l-1\)的前缀和。
修改
对于\(sum1\)数组的修改同问题2中对d数组的修改。
对于\(sum2\)数组的修改也类似,我们给 $sum2[l] \(加上\) l * x\(,给\) sum2[r + 1] \(减去\) (r + 1) * x$。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号