线性筛,整除分块,欧拉函数与莫比乌斯反演
埃氏筛法
说到筛质数,就不得不提到大名鼎鼎的埃氏筛法了
思想非常简单,就是对于每一个素数pri[i],我们都把它的倍数筛去,
譬如对于素数2来说,我们就把\(2*2, 2*3, 2*4, 2*5 .... 2*n\) 的数全部筛掉
代码
void zhishu(int n){
for(int i=2;i<=n;i++){
if(p[i]==0)
for(int j=i*2;j<=n;j+=i)
p[j]=1;
}
}
实际上我们可以发现,对于30来说,它被2筛过,被3筛过,被5筛过,
显然这种算法并不是最优的,因为对于同样的一个数,它被筛了多次
它的时间复杂度是\(O(n\ log\ log n)\)
线性筛
分析
对于每一个数,我们都希望它只被它最小的质因子筛掉,
譬如说我们希望18被2筛掉,而不是被3筛掉,
而30被2筛掉,不是被3,5筛掉
举个例子,当\(pri[]={2,3,5},i=6\)时,我们先把$12=2*6 $筛去,
但是我们发现,对于$18=3 * 6 $来说,我们没有必要把18筛掉,
因为$ 18=3* 6=3(3 2)=2 * 9 $,也就是说当i=9的时候,我们会把\(18=2* 9\)筛掉,所以现在就没有必要筛掉18
对于 i%prime[j] ==0 就break的解释 :
当 i是prime[j]的倍数时,i = k * prime[j],
如果继续运算 j+1,i * prime[j+1] = prime[j] * k * prime[j+1],
这里i * prime[j+1] 应该被 prime[j] 筛掉而不是prime[j+1]
所以才跳出循环。
因此,对于任意一个数,它都会只访问一次,所以时间复杂度就达到了\(O(n)\)的级别
欧拉筛还有一个优点,就是它在筛质数的过程中会把质数都存储下来,就比埃氏筛法更加的方便
线性筛的本质就是对于一个i,我们先把质数表中和i互质的数筛掉,然后再筛一个最大公约数为当前质数的数就退出循环
代码
void ols(){
for(int i=2;i<=n;i++){
if(!d[i])pri[++len]=i;
for(int j=1;pri[j]*i<=n&&j<=len;j++){
d[pri[j]*i]=true;
if(i%pri[j]==0)break;
}
}
}
欧拉函数
欧拉函数\(φ(n)\)表示小于等于n,且与n互质的正整数的个数。
如何求\(φ(n)\)?
比如\(φ(12)\)
把12质因数分解,\(12=2^2*3\),其实就是得到了2和3两个互异的质因子
然后把2的倍数和3的倍数都删掉
2的倍数:\(2,4,6,8,10,12\)
3的倍数:\(3,6,9,12\)
但是是6和12重复减了
所以还要把即是2的倍数又是3的倍数的数加回来
所以这样写\(12 - \frac{12}{2} -\frac{ 12}{3} +\frac{ 12}{2*3}\)
这是容斥原理!
特别地, \(\varphi(1) = 1\)

代码
//求n的欧拉函数值: phi[n]
int getPhi(int n){
int ans = n;
for(int i = 2; i*i <= n; i++){
if(n % i == 0){
ans = ans * (i-1)/i;
while(n % i == 0) n /= i;
}
}
if(n > 1) ans = ans * (n-1)/n ;
return ans;
}
//时间复杂度:sqrt(n)
欧拉函数的一些性质
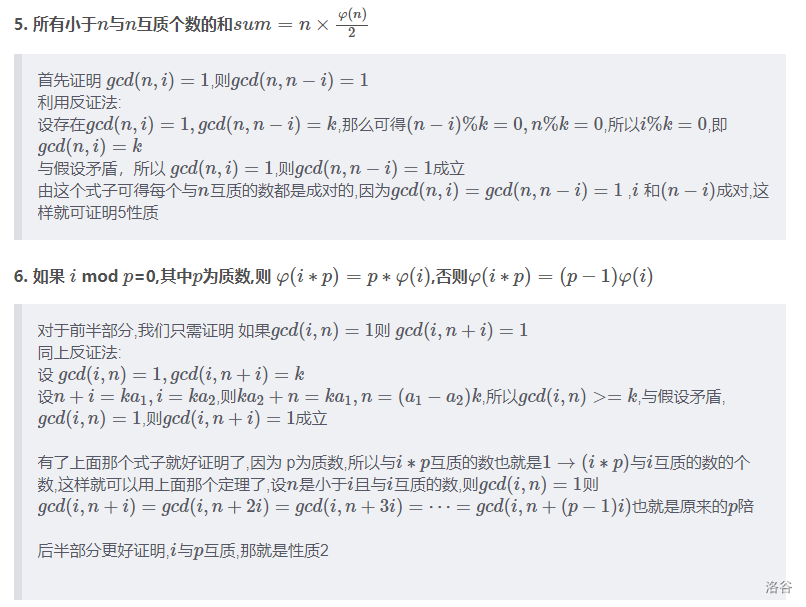
性质
1、\(对于任意一个质数p,\varphi(n)=n-1\)
2、\(当gcd(n,m)=1时,\varphi(nm)=\varphi(n)\varphi(m)\)
3、\(若n=p^k 其中p为质数,则\varphi(n)=p^k-p^{k-1}=(p-1)p^{k-1}\)
4、$n= p_1{k_1}p_2 \dots p_{m-1}{k_{m-1}}p_m 其中 p_m^{k_m} 为n所分解的质因数(k_m为每个质因数的个数) ,则\varphi(n) = n \prod_{i=1}^m(1- \frac{1}{p_i}) $
5、\(所有小于n与n互质的数的和sum=n \times \frac{\varphi(n)}{2}=\sum\limits_{d=1}^{n}[gcd(d,n)=1]\)
6、\(如果i\mod p = 0,其中p为质数则\varphi(i*p)=p*\varphi(i)否则\varphi(i*p)=(p-1)\varphi(i)\)
7、\(n= \sum_{d|n}\varphi(d)\)
8、$欧拉定理:对于互质的整数a,m,有a^{\varphi(m)} \equiv 1 $
9、\(欧拉降幂公式 A^K\equiv A^{K \%\phi(m) +\phi(m)}(\mod \ m);\)$ K > \phi(m) $
10、\(\varphi(a*b)=\varphi(a)*\varphi(b)*\frac{d}{\varphi(d)},其中d=gcd(a,b)\)
证明


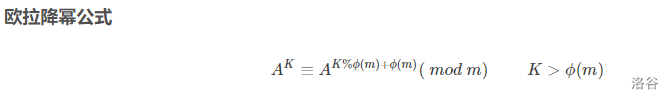

积性函数
定义
性质
若$ f(n)$和 \(g(n)\) 都是积性函数,则以下函数也为积性函数:
积性函数的证明

P1403 [AHOI2005]约数研究(数据范围1e7)



艾佛森括号
此处 \(P\)是一个可真可假的命题。
整除分块
时间复杂度
时间复杂度\(O(\sqrt n)\),证明见下
引理
证明


关于右端点r的证明
\(首先,我们已经知道上一个端点的r,那我们现在的l=r+1,因此我们可以得到现在的值\)\(k=\left \lfloor \dfrac nl\right\rfloor\)
而\(\lfloor\frac{n}{l}\rfloor=\lfloor\frac{n}{r}\rfloor=k\)
实际上就是\(k \leq \frac{n}{l} \leq \frac{n}{r} < k+1\)
显然,我们需要找到一个r,使得\(r*k\leq n\),所以\(r=\left \lfloor \dfrac nk\right\rfloor\)
所以最终我们就有
\(r=\left \lfloor \dfrac {n}{\left \lfloor \dfrac nl\right\rfloor}\right\rfloor\)
例题一 H(n)
代码
#include<bits/stdc++.h>
using namespace std;
long long t,n,ans,l,r,k;
int main(){
cin>>t;
while(t--){
cin>>n;
r=0;
ans=0;
while(r+1<=n){
l=r+1;
k=n/l;
r=min(n,n/k);
ans+=k*(r-l+1);
}
cout<<ans<<endl;
}
return 0;
}
例题二 P2261 [CQOI2007]余数求和
分析
对于这题而言,我们显然有
\(ans=\sum\limits_{i=1}^{n}k-i*\lfloor\frac{k}{i}\rfloor=n*k-\sum\limits_{i=1}^{n}i*\lfloor\frac{k}{i}\rfloor\)
所以我们只用分块计算\(\sum\limits_{i=1}^{n}i*\lfloor\frac{k}{i}\rfloor\)即可
显然,对于其中的第一项\(i\)我们可以很好地进行计算,主要是后面的\(\sum\limits_{i=1}^{n}\lfloor\frac{k}{i}\rfloor\)我们要如何计算
考虑我们已知\(l\),求\(r\),显然,当前的\(num=\lfloor\frac{k}{l}\rfloor\)
而\(\lfloor\frac{k}{l}\rfloor=\lfloor\frac{k}{r}\rfloor=num\),实际上就是\(num \leq \frac{k}{l} \leq \frac{k}{r} < num+1\)
因此就有\(num \leq \frac {k}{r}\),所以$r \leq \frac {k}{num} \(,最终有\)r=\lfloor\frac{k}{num}\rfloor $
所以最终是\(r=\left \lfloor \dfrac {k}{\left \lfloor \dfrac kl\right\rfloor}\right\rfloor\),而不是\(r=\left \lfloor \dfrac {n}{\left \lfloor \dfrac kl\right\rfloor}\right\rfloor\)
还有一个问题,当\(num=0\)时,求和项一定为0,所以我们不用去计算它的\(r\),还要注意\(r\)要和\(n\)取\(min\)
实际上我们还可以这样考虑:当$n\leq k \(时,直接计算便可,当\)n > k\(时,\)\lfloor\frac{k}{i}\rfloor=0\(所以显然是\)r=\left \lfloor \dfrac {k}{\left \lfloor \dfrac kl\right\rfloor}\right\rfloor$
代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,k,l,r,num=0,ans=0;
signed main(){
cin>>n>>k;
r=0;
while(r+1<=n){
l=r+1;
num=k/l;
if(num==0)break;
r=min(n,k/(k/l));
ans=ans+(r+l)*(r-l+1)/2*num;
}
cout<<n*k-ans;
return 0;
}
扩展
分块的实质就是把能分块的求出来,然后剩下的项我们先预处理前缀和,然后计算贡献
有时候我们要求形如\(\sum\limits_{T=1}^{n}\left\lfloor\frac{n}{T}\right\rfloor\left\lfloor\frac{m}{T}\right\rfloor\)的式子,实际上就是把相交的部分一起计算
理论上时间复杂度最大为\(O(4\sqrt n)\)
代码
cin>>n>>m;
if(n>=m)swap(n,m);
int l,r=0,num1,num2,r1,r2;
while(r+1<=n){
l=r+1;
num1=n/l,num2=m/l;
r1=n/num1,r2=m/num2;
r=min(n,min(r1,r2));
ans+=num1*num2*(sum_f[r]-sum_f[l-1]);
}
cout<<ans<<endl;
莫比乌斯函数


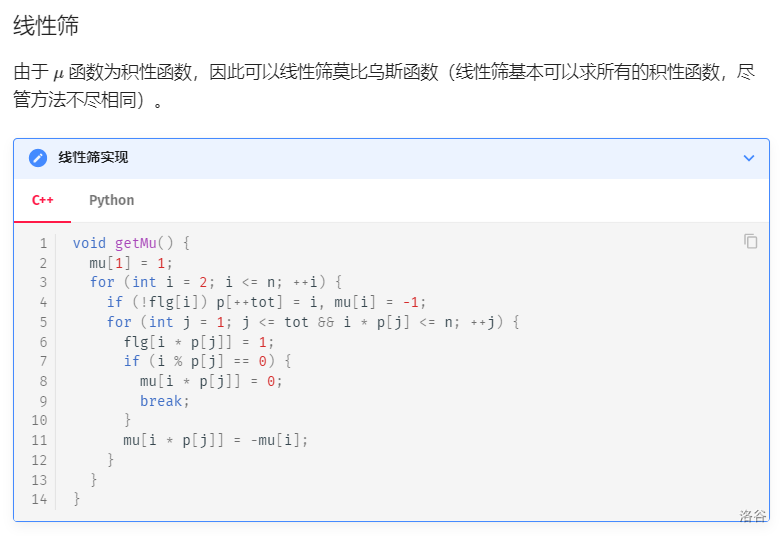
莫比乌斯反演
其实并没有什么用
形式一
如果有
$ f(n)=\sum\limits_{d|n}g(d)$
就有
$ g(n)=\sum\limits_{d|n} \mu(d)f(\frac{n}{d})$
\(这种形式下,数论函数f(n)称为数论函数 g(n) 的莫比乌斯变换,数论函数 g(n)称为数论函数 f(n)的莫比乌斯逆变换(反演)。\)
形式二
如果有
$ f(n)=\sum\limits_{n|d}g(d)$
就有
$ g(n)=\sum\limits_{n|d} \mu(\frac{d}{n})f(d)$
做题中最重要的公式
1、$ [n=1]=\sum\limits_{d| n} \mu(d)$
证明:

2、$ n=\sum\limits_{d|n}\varphi(d)$
设一个集合\({1/n,2/n,3/n,...,(n-1)/n,n/n}\)
对于上述的分式集合,若我们都将其化简至最简形式,设其中一个最简形式是a/b,那么我们一定有:
$b|n $①
\((a,b)=1\) ②
\(a<=b\) ③
由②③可得,对于一个确定的b,它对应的a的个数为\(\varphi(b)\)(根据欧拉函数的定义:φ(n)=1到n中与n互质的数的个数)
那么我们再考虑,每一个最简形式a/b都是互相不同的,因为它们都是最简形式
而且,对于上述分数集合来说每一个元素都可以化简成最简形式(完备性),而元素的个数正好就是n
于是定理得证
3、\(\frac{\varphi(n)}{n}=\sum\limits_{d|n}\frac{\mu(d)}{d}\)
考虑证明该式子
欧拉函数的定义式\(\varphi(n)=\sum\limits_{i=1}^{n}[gcd(n,i)=1]\)
莫比乌斯函数的求和式$ [n=1]=\sum\limits_{d| n} \mu(d)$
我们用\(gcd(n,i)\)代替\(n\)就有
$ [gcd(n,i)=1]=\sum\limits_{d|gcd(n,i)} \mu(d)$
所以
所以就有\(\frac{\varphi(n)}{n}=\sum\limits_{d|n}\frac{\mu(d)}{d}\)
手推式子(默认\(n\leq m\))
一些基础的东西
1、\([n|\gcd(a,b)]\iff[n|a][n|b]\)
令\(a=dp,b=dq\),其中\(\gcd(p,q)=1\)
考虑证明充分性
当\(n|\gcd(a,b)\)时,就相当于\(n|d\)
\([n|\gcd(a,b)]=[n|d]\)
\([n|a][n|b]=[n|dp][n|dq]\)
若\([n|d]=1,则[n|dp][n|dq]=1\)
若\([n|d]=0,则n \nmid d,若要使[n|dp][n|dq]=1,则要n\mid p 且n\mid q ,又因\gcd(p,q)=1,所以n=1,[n|d]=1,矛盾\)
所以充分性得证
考虑证明必要性
若有\([n|a][n|b],则有[n|dp][n|dq]\)
若\(n|d,则命题得证\)
若\(n\nmid d,则有[n|p][n|q],且[n|\gcd(a,b)]=0\)
若此时\([n|p][n|q]=1,则由\gcd(p,q)=1,有n=1,但此时[1|\gcd(a,b)]=1,矛盾\)
故得证
2、\(f(x)=\sum\limits_{i=1}^{n}[x|i]=\lfloor \frac nx \rfloor\)
用人话来说就是求1到n中x的倍数,证明显然
例题一 P3935 Calculating
若\(x\)分解质因数的结果为\(x=\prod\limits_{i=1}^{z}{p_i}^{k_i}\),令\(f(x)=\prod\limits_{i=1}^{z}(k_i+1)\)
求\(\sum\limits_{i=l}^{r}f(i)\)对\(998244353\)取模的结果
上面的可以简化为:
考虑求
最后再数论分块即可。
时间复杂度 \(\mathcal O(\sqrt{n})\)。
例题二 P2260 [清华集训2012]模积和
求
mod 19940417 的值
首先不妨设\(n<m\)
注意到后面的\(i \neq j\),则可以将式子变成
然后显然就有
根据取模的定义,\(a \bmod b=a-b \times \left\lfloor\frac{a}{b}\right\rfloor\),就有
拆括号
例题三
考虑使用公式$ [n=1]=\sum\limits_{d| n} \mu(d)$进行化简
例题四
化简
方法一(采用欧拉函数):
方法二(采用莫比乌斯函数):
例题五
化简
方法:
例题六 P1829 [国家集训队]Crash的数字表格 / JZPTAB
求(对 20101009 取模):
方法:
易得:
例题七
题目描述
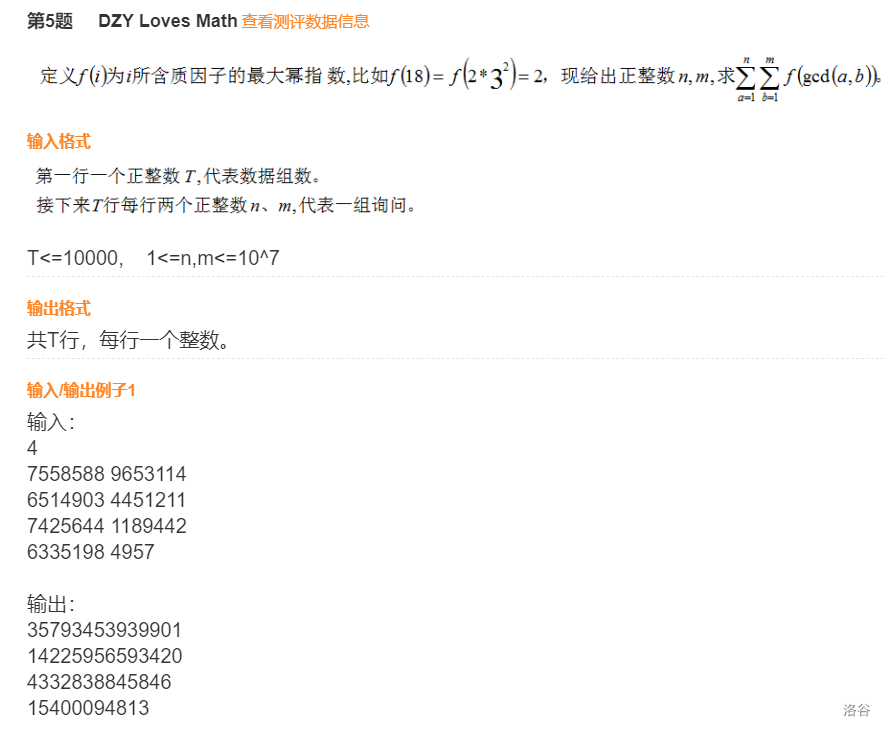
分析
实际上这个就是例题五,重要的是我们要怎么处理最后的$$\sum\limits_{k|T}\mu(\frac{T}{k})f(k)$$
考虑如下操作
代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=1e7+10,maxm=664579+10;
int g[maxn],gg[maxn],MAX[maxn],f[maxn],sum_f[maxn];
bool vis[maxn]={false};
int pri[maxm],cnt=0;
int T,n,m;
void init(){
g[1]=1;
gg[1]=1;
MAX[1]=0;
f[1]=-1;
sum_f[1]=0;
for(int i=2;i<=maxn;i++){
if(!vis[i]){
pri[++cnt]=i;
g[i]=i;
gg[i]=1;
MAX[i]=1;
f[i]=1;
// cout<<i<<" ";
}
for(int j=1;j<=cnt&&pri[j]*i<=maxn;j++){
int num=pri[j]*i;
vis[num]=true;
if(i%pri[j]==0){
g[num]=pri[j]*g[i];
gg[num]=gg[i]+1;
MAX[num]=max(MAX[num/g[num]],gg[num]);
f[num]=(f[num/g[num]]!=0&&(gg[num]==MAX[num/g[num]]||num/g[num]==1))?(-f[num/g[num]]):0;
break;
}
g[num]=pri[j];
gg[num]=1;
MAX[num]=max(MAX[num/g[num]],1ll);
f[num]=(f[num/g[num]]!=0&&(gg[num]==MAX[num/g[num]]||num/g[num]==1))?(-f[num/g[num]]):0;
}
sum_f[i]=sum_f[i-1]+f[i];
// cout<<i<<" "<<g[i]<<" "<<gg[i]<<" "<<MAX[i]<<" "<<f[i]<<endl;;
}
return ;
}
signed main(){
// cin>>n>>m;
init();
cin>>T;
while(T--){
int ans=0;
cin>>n>>m;
if(n>=m)swap(n,m);
int l,r=0,num1,num2,r1,r2;
while(r+1<=n){
l=r+1;
num1=n/l,num2=m/l;
r1=n/num1,r2=m/num2;
r=min(n,min(r1,r2));
ans+=num1*num2*(sum_f[r]-sum_f[l-1]);
}
cout<<ans<<endl;
}
// cout<<cnt<<endl;
// cout<<ans;
return 0;
}
例题八 P3312 [SDOI2014]数表
代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=1e5+10,maxm=664579+10,maxT=2*1e4+5;
int g[maxn],mu[maxn],ANS[maxn];
bool vis[maxn]={false};
int pri[maxm],cnt=0;
int TT,n,m;
struct edge{
int v,pos;
}f[maxn];
bool cmp2(edge x,edge y){
if(x.v==y.v)return x.pos<y.pos;
return x.v<y.v;
}
void init(){
mu[1]=1;
g[1]=1;
f[1].v=1;
f[1].pos=1;
for(int i=2;i<=maxn;i++){
if(!vis[i]){
pri[++cnt]=i;
mu[i]=-1;
g[i]=i;
f[i].v=i+1;
// cout<<i<<" ";
}
for(int j=1;j<=cnt&&pri[j]*i<=maxn;j++){
int num=pri[j]*i;
vis[num]=true;
if(i%pri[j]==0){
mu[num]=0;
g[num]=g[i]*pri[j];
f[num].v=f[i].v+f[num/g[num]].v*g[num];
break;
}
mu[num]=-mu[i];
g[num]=pri[j];
f[num].v=f[i].v*(pri[j]+1);
}
f[i].pos=i;
// cout<<i<<" "<<g[i]<<" "<<f[i].v<<endl;;
}
return ;
}
struct node{
int x,y,lim,pos;
}a[maxn];
bool cmp1(node x,node y){
return x.lim<y.lim;
}
struct Tree{
int tr[maxn];
void update(int now,int num){
for(;now<=maxn;now+=now&(-now))tr[now]+=num;
return ;
}
int check(int now){
int ans=0;
for(;now>0;now-=now&(-now))ans+=tr[now];
return ans;
}
}T;
signed main(){
// cin>>n>>m;
init();
sort(f+1,f+maxn+1,cmp2);
// for(int i=1;i<=maxn;i++)cout<<f[i].pos<<" "<<f[i].v<<endl;
cin>>TT;
for(int i=1;i<=TT;i++){
cin>>a[i].x>>a[i].y>>a[i].lim;
a[i].pos=i;
if(a[i].x>a[i].y)swap(a[i].x,a[i].y);
}
sort(a+1,a+TT+1,cmp1);
int now=0;
for(int i=1;i<=TT;i++){
while(f[now+1].v<=a[i].lim){
now++;
// cout<<f[now].pos<<" "<<f[now].v<<endl;
for(int j=1;j*f[now].pos<=maxn;j++)
T.update(j*f[now].pos,f[now].v*mu[j]);
}
// cout<<"FA";
int ans=0;
int l,r=0,num1,num2,r1,r2;
while(r+1<=a[i].x){
l=r+1;
num1=a[i].x/l,num2=a[i].y/l;
r1=a[i].x/num1,r2=a[i].y/num2;
r=min(a[i].x,min(r1,r2));
ans+=num1*num2*(T.check(r)-T.check(l-1));
}
ANS[a[i].pos]=ans;
}
for(int i=1;i<=TT;i++)cout<<(ANS[i]%(1<<31))<<"\n";
return 0;
}
做题中我们如何预处理前缀和
对于式子
显然是积性函数
我们可以在线性筛的过程中计算出来
我们分类讨论
1,当\(T\)为质数时,\(f(T)=\mu(1)*1+\mu(T)*T=1-T\)
2,当\(i\)与\(p\)互质时,\(f(i*p)=f(i)*f(p)\)
3,当\(\gcd(i,p)=p\)时:设\(i=p^m*i'\)
所以对于这种要预处理的式子,我们先讨论\(n=p(p为质数)\)的情况,然后讨论另外的情况


 浙公网安备 33010602011771号
浙公网安备 33010602011771号