二叉树

二叉树：

　　满足以下条件的树就是二叉树：

　　1. 本身是有序树 （ 二叉树的数据结构是树）

　　2. 树中包含各个节点的度不超过2. 度只能是 0 ，1，2

 

二叉树的五种基本形态 ：

　　1. 空树

　　2. 只有根节点的树

　　3. 有根且只有左子树

　　4. 有根且只有右子树

　　5. 有根且有一个左子树，有一个右子树

 

二叉树特点：

　　1. 二叉树中，第 i 层最多有 2^i–1 个结点。
　　2. 如果二叉树的深度为 K，那么此二叉树最多有 2^k–1个结点。
　　3. 二叉树中，终端结点数（叶子结点数）为 n0，度为 2 的结点数为 n2，则 n0=n2+1。

　　性质 3 的计算方法为：对于一个二叉树来说，除了度为 0 的叶子结点和度为 2 的结点，剩下的就是度为 1 的结点（设为 n₁），那么总结点 n=n₀+n₁+n₂。

满二叉树：

　　如果二叉树中除了叶子结点，每个结点的度都为 2，则此二叉树称为满二叉树。

　　

 

 

　　

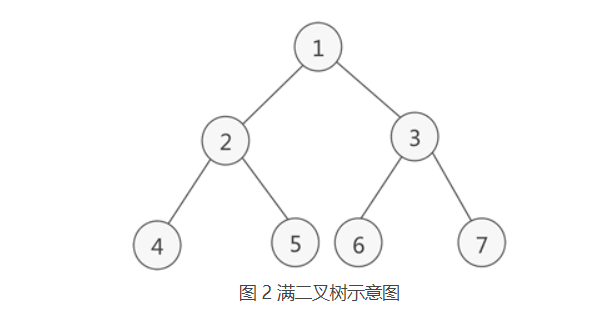
完全二叉树：

　　如果二叉树中除去最后一层节点为满二叉树，且最后一层的结点依次从左到右分布，则此二叉树被称为完全二叉树。

 

 

 

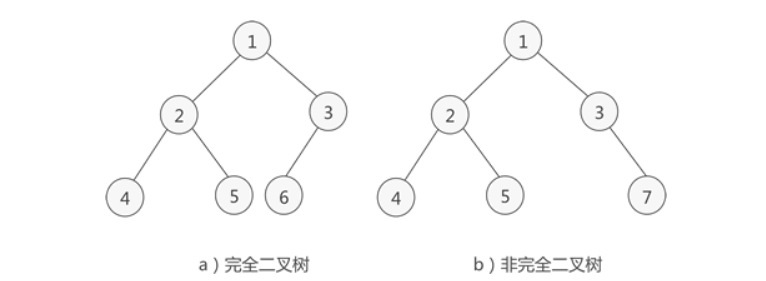
 　　完全二叉树除了具有普通二叉树的性质，它自身也具有一些独特的性质，比如说，n 个结点的完全二叉树的深度为 ⌊log₂n⌋+1。

　　⌊log₂n⌋ 表示取小于 log₂n 的最大整数。例如，⌊log₂4⌋ = 2，而 ⌊log₂5⌋ 结果也是 2。

 　　对于任意一个完全二叉树来说，如果将含有的结点按照层次从左到右依次标号（如图 3a)），对于任意一个结点 i ，完全二叉树还有以下几个结论成立：

　　

　　　　当 i>1 时，父亲结点为结点 [i/2] 。（i=1 时，表示的是根结点，无父亲结点）
　　　　如果 2*i>n（总结点的个数） ，则结点 i 肯定没有左孩子（为叶子结点）；否则其左孩子是结点 2*i 。
　　　　如果 2*i+1>n ，则结点 i 肯定没有右孩子；否则右孩子是结点 2*i+1 。

 

二叉排序树

　　又叫二叉搜索树,  二叉查找树

　　二叉排序树或者是一棵空树； 或者是具有下列性质的二叉树：

　　　　(1)若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；

　　　　(2)若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；

　　　　(3)它的左、右子树也分别为二叉排序树。

平衡二叉树

• 1. 是「二叉排序树」
• 2. 任何一个节点的左子树或者右子树都是「平衡二叉树」（左右高度差小于等于 1）