KMP算法讲解

什么是 KMP 算法

KMP 算法要解决的问题就是在字符串中的模式串定位问题。说简单点就是我们平时常说的关键字搜索。模式串就是关键字（接下来称它为 \(P\) ），如果它在一个主串（接下来称为 \(T\) ）中出现，就返回它的具体位置，否则返回 \(-1\) （常用手段）。

暴力思路

假设现在文本串 \(T\) 匹配到 \(i\) 位置，模式串 \(P\) 匹配到 \(j\) 位置，则有：

• 如果当前字符匹配成功（即 \(T[i] == P[j]\) ），则 i++,j++，继续匹配下一个字符
• 如果失配（即 \(T[i]! = P[j]\) ），则 \(i\) 回溯， \(j\) 被置为 \(1\)，即 i=i-j+1,j=1

code:

int i=1,j=1;
while(i<=n && j<=m){
    if(T[i]==P[j]) i++,j++;
    else i=i-j+1,j=1;
}
if(j>n) return i-j;
else return -1;

时间复杂度： \(O(n m)\)

正解

首先，为什么暴力的模式匹配这么慢呢？你再回头看一遍就会发现，原来是回溯的步骤太多了。所以我们应该尽量减少回溯的次数。

观察下图的例子：

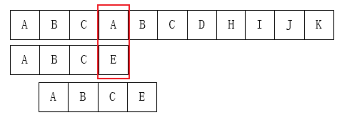
我们发现，如果是人来找，肯定不会再将 \(i\) 放回第 \(2\) 位了，因为在主串匹配失败的位置以前除了第一个 A 外没有其他 A 了。

我们为什么能知道主串前面只有一个 A ？ 因为我们已经知道前面三个字符都是匹配的！。移动过去肯定也是不匹配的！

所以，有一个想法， \(i\) 不移动，只移动 \(j\) 。

由此 KMP 诞生了。

所以，整个 KMP 的重点就在于当某一个字符与主串不匹配时，我们应该知道 \(j\) 指针要移动到哪？

那么我们先自己找一下 \(j\) 的移动规律。

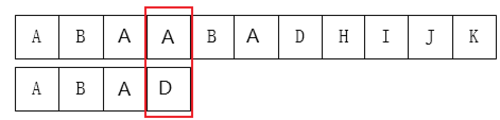
如图：A 和 D 不匹配了，我们要把 \(j\) 移动到哪？显然是第 \(2\) 位。为什么？因为前面有一个 A 相同，

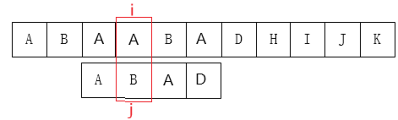
至此我们可以大概看出一点端倪，当匹配失败时， \(j\) 要移动的下一个位置 \(k\)。存在着这样的性质：\(j\) 前面的 \(k\) 个字符和 \(i\) 之前的最后 \(k\) 个字符是一样的。

又看到上图，发现之所以可以直接把 \(j\) 移到 \(k\) ，是因为我们已经保证上述性质。即保证 \(P\) 的前缀一定在 \(T\) 上以 \(i\) 结尾的后缀上匹配成功了。我们再观察一下 \(T\) 上以 \(i\) 结尾的后缀，发现一个点 —— \(T\) 以 \(i\) 为结尾的后缀必然在 \(P\) 的前缀中

看图理解：

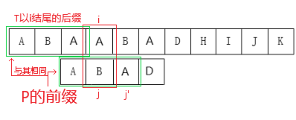
其中 \(j'\) 表示上一次匹配时的 \(j\) 。

于是我们发现，这不就是在求公共前后缀吗？

那么我们定义一个 \(ne\) 数组，（后文用 \(k\) 表示）， 那么 \(ne_j\) 的值（即 \(k\) ）表示，当 \(P_j \ne T_i\) 时，\(j\) 指针的下一步移动位置。

那具体如何求解 \(ne\) 数组呢？

先来看一种情况：当 \(j\) 为 \(1\) 时，如果这时候不匹配，怎么办？

\(j\) 已经在最左边了，不可能再移动了，这时候要应该是 \(i\) 指针后移，所以有 ne[1]=0

那么 \(j \ne 1\) 呢？

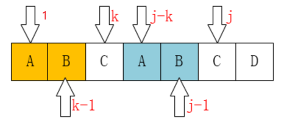
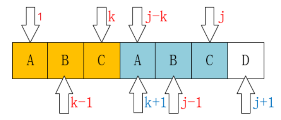
请仔细对比这两个图。

我们发现一个规律：

​ 当 \(P_k = P_j\) 时，

​ 有 \(ne_{j+1} = ne_{j} + 1\)

其实这个是可以证明的：

​ 因为在 \(P_j\) 之前已经有 \(P_{0 \sim k-1} = P_{(j-k) \sim (j-1)}\) 。（\(ne_j = k\)）

​ 这时候现有 \(P_k = P_j\)，我们是不是可以得到 \(P_{0 \sim (k-1)} + P_k = P_{(j-k) \sim (j-1)} + P_j\)。

​ 即 \(P_{0 \sim k} = P_{(j-k) \sim j}\)

​ 即 $ ne_{j+1} = k + 1 = ne_j + 1$。

还是看图会容易理解些......

当 \(P_k \ne P_j\)

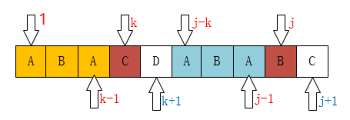
像这种情况，如果你从代码上看应该是这一句：j=ne[j]，为什么呢？

现在你应该知道为什么要 j=ne[j]了，像上边的例子，我们已经不可能找到 [ A，B，A，B ] 这个最长的后缀串了，但我们还是可能找到 [ A，B ] 、 [ B ] 这样的前缀串的。所以这个过程像不像在定位 [ A，B，A，C ] 这个串，当 C 和主串不一样了（也就是k位置不一样了），就该把指针移动到 \(ne_j\) 了。

有了 \(ne\) 数组之后就一切好办了，我们可以动手写 KMP 了

 	ne[1]=0;//初始化
    for(int i=2,j=0;i<=m;i++){//求ne数组
        while(j && v[i]!=v[j+1]) j=ne[j];
        if(v[i]==v[j+1]) j++;
        ne[i]=j;
    }
    for(int i=1,j=0;i<=n;i++){
        while(j && u[i]!=v[j+1]) j=ne[j];
        if(u[i]==v[j+1]) j++;
        if(j==m) cout<<i-j+1<<'\n';//输出P在T中的位置
    }

对于 \(ne\) 数组的使用，按照之前所说，只要当前 \(T_i \ne P_j\) ，就开始下一轮匹配。将 \(j\) 指针一直跳 \(ne_j\) ，直到 \(T_i=P_{j+1}\) （即当前位匹配成功），就继续向后匹配。

例题

P4391 [BalticOI 2009] Radio Transmission 无线传输

这是一道经典 KMP 的应用，对于理解 \(ne\) 数组有着很大帮助。

我们尝试求题目所给的字符串的 \(ne\) 数组，当我们看到 \(ne_n\) 时，有一个惊人的发现：

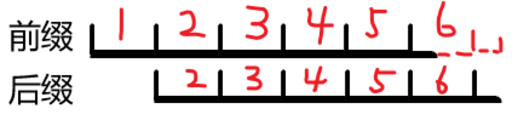
对于 \(ne_n\) （即上图所示），我们将其前缀和后缀分为很多相同的小块，即题目中所求的小块。

如图，我们发现，图中第一块小块的长度就是 \(n-ne_n\) ！！！就是字符串原长度减去 \(ne_n\) 的后缀的长度。

从而，我们知道了原字符串除去公共前后缀（图中的后缀）中的一个剩下的就是循环子串。

那么 \(ans=n-ne_n\)

P5256 [JSOI2013] 编程作业

这道题的难点在于相等的定义有所改变。

那如果相等的定义不变，这道题该怎么做呢？

很明显，用 KMP 直接匹配就可以了。

那我们现在的问题就变成了如何去将相等转化为 KMP 中可以使用的相等

直接给思路： 将每个点从字符变成当前这个字符到下一个与他相同的字符的距离。如果之后没有与他相同的，那直接置为 \(0\) ，不用管他。接下来直接进行 KMP 就可以了。

之所以能想到这个方法，是因为在题目中，字符是什么并不重要，重要的是其所在的所有位置，即当前字符与和他相同字符的关联。