计算二叉树最大宽度

求非空二叉树的宽度

非递归实现

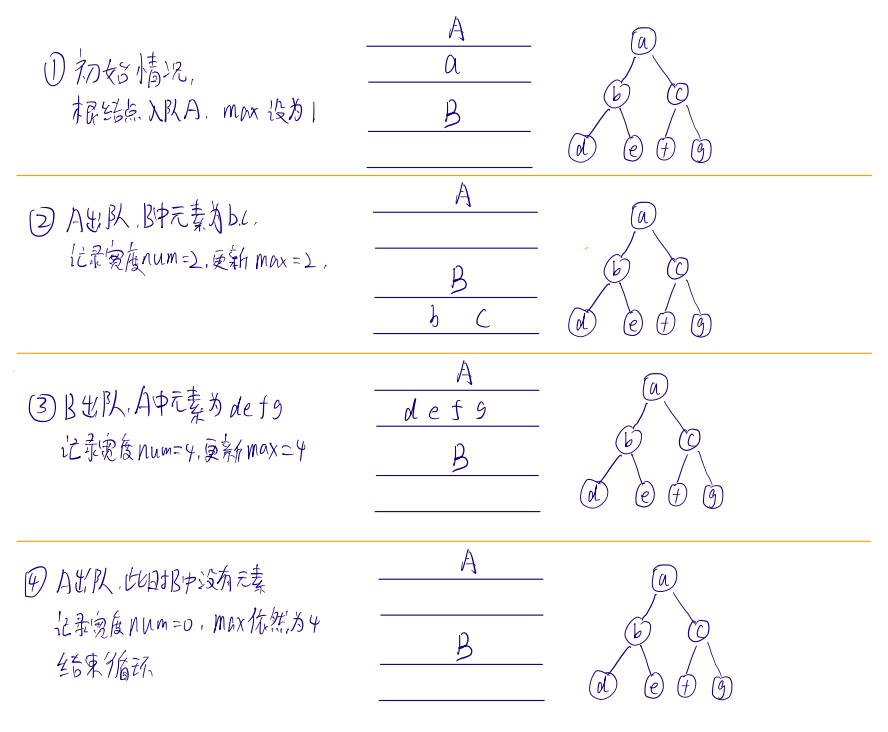
算法思想：层序遍历二叉树，并用两个队列A,B交替存储结点，当队列A中元素为空时队列B就存储了下一层的所有结点，同理，队列B为空时队列A也就存储了下一层的所有结点。记录每层的最大宽度并与当前最大宽度比较并更新最大宽度，遍历完所有结点后即可求出最大宽度。

int BTWidth(BiTree bt){
    int max=0,num=0;
    InitQueue(A); InitQueue(B);          //初始化A B两队列
    EnQueue(A,bt); max++;                //先让根节点入队，并让max=1
    BiTree p;                            //定义p指针用来出队或入队
    while(!IsEmpty(A)||!IsEmpty(B)){     //当两个队列都为空时结束循环
        if(!IsEmpty(A)){
            num=0;
            while(!IsEmpty(A)){              //A出队，记录B中的宽度
                DeQueue(A,p)                 //让A的对头出队并用p指向他
                if(p->lchild){               //若有左孩子，则左孩子进入队B
                    EnQueue(B,p->lchild);   
                    num++;
                }    
                if(p->rchild){               //若有右孩子，则右孩子进入队B
                    EnQueue(B,p->rchild);
                    num++;
                }
            }
            max=(max>num)?max:num;       //更新最大宽度(与B中宽度比较)
        }
        if(!IsEmpty(B)){
            num=0;
            while(!IsEmpty(B)){              //B出队，记录A中的宽度
                DeQueue(B,p)                 
                if(p->lchild){               //若有左孩子，则左孩子进入队A
                    EnQueue(A,p->lchild);
                    num++;
                }
                if(p->rchild){               //若有右孩子，则右孩子进入队A
                    EnQueue(A,p->rchild);
                    num++;
                }
            }
            max=(max>num)?max:num;       //更新最大宽度(与A中宽度比较)
        }
    }
    return max;
}

递归实现

引用自https://blog.csdn.net/mcb199175mcb/article/details/12031217

算法思想:开辟一个数组count[二叉树高度],遍历每一个节点,然后根据当前节点所在层次i,则执行count[i]++;

最后遍历完求出最大的count即为二叉树宽度

代码如下

int  count[100];
int MAX=-1;
 
void FindWidth(BitNode T,int k)       //k用来记录深度
{
	if(T==NULL)  return;
	count[k]++;
	if(MAX<count[k]) MAX=count[k];
	FindWidth(T->lchild,k+1);
	FindWidth(T->rchild,k+1);
}
 
//MAX即为所求宽度