求树的高度和结点层数

求树的高度

递归实现

代码思路：检查结点的左右子树，让高度较大的子树加上1即为树的高度，然后递归的重复此过程

int Btdepth(BiTree T){
    if(T==NULL)                      //递归的出口
        return 0;
    ldep=Btdepth(T->lchild);         //左子树的高度
    rdep=Btdepth(T->rchild);         //右子树的高度
    if(ldep>rdep)                    //返回较大子树的高度加上1
        return ldep+1;
    else
        return rdep+1;
}

非递归实现

代码思路：层序遍历二叉树，若遍历完一层的最后一个结点时让记录的高度加1

1. 用层序遍历二叉树，需要用到队列，并用front和rear来表示当前队列中的情况
   (注意front和rear初始为-1，因为需要判定front==last时到达此层最后一个结点)
2. 用一个last指针指向每层的最后一个结点，初始时指向根节点last=0，即队中Q[0]的位置
3. 用level来记录当前树的高度

int Btdepth(BiTree T){
    if(T==NULL)
        return 0;           //如果为空树返回高度0
    int front=-1,rear=-1;   //初始化队列中的参数
    int level=0,last=0;     //初始化树的高度和last标记
    BiTree Q[Maxsize];      //设置队列，因为要存放的元素是树的结点所以用BiTree来定义
    Q[++rear]=T;            //先让根节点入队
    BiTree p;               //用一个p指针来遍历二叉树
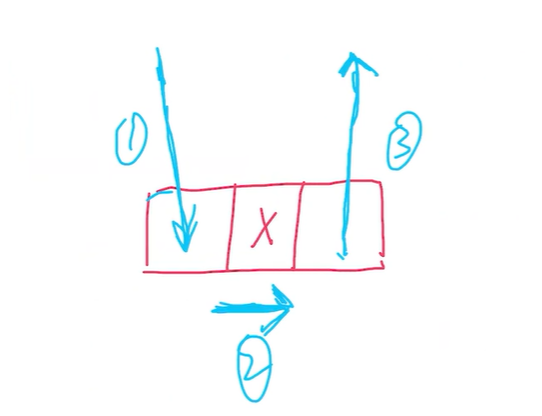
    while(front<rear){      //当队不空时循环
        p=Q[++front];                  //出队
        if(p->lchild)                  //若有左孩子则左孩子入队
            Q[++rear]=p->lchild;
        if(p->rchild)                  //若有右孩子则右孩子入队
            Q[++rear]=p->rchild;
        if(front==last){               //若此次出队的结点是此层最后一个结点
            level++;                   //树的高度加1
            last=rear;                 //让last指向下一层的最后一个结点
        }
    } 
    return level;
}

小疑问

Q：为什么last每次都能指向每层的最后一个结点呢φ(゜▽゜*)♪？

A：我们不妨来模拟一下，每次front移动的时候都会让rear指向它最后一个孩子（从左向右数），当front第一次等于last的时候，rear指向第二层的最后一个，当front第二次等于last的时候，rear指向第三层的最后一个结点，以此类推每次front指向上一层的最后一个结点的时候rear就指向下一层的最后一个结点啦Ψ(￣∀￣)Ψ，此时只要让last等于rear就能更新每层最后一个结点。

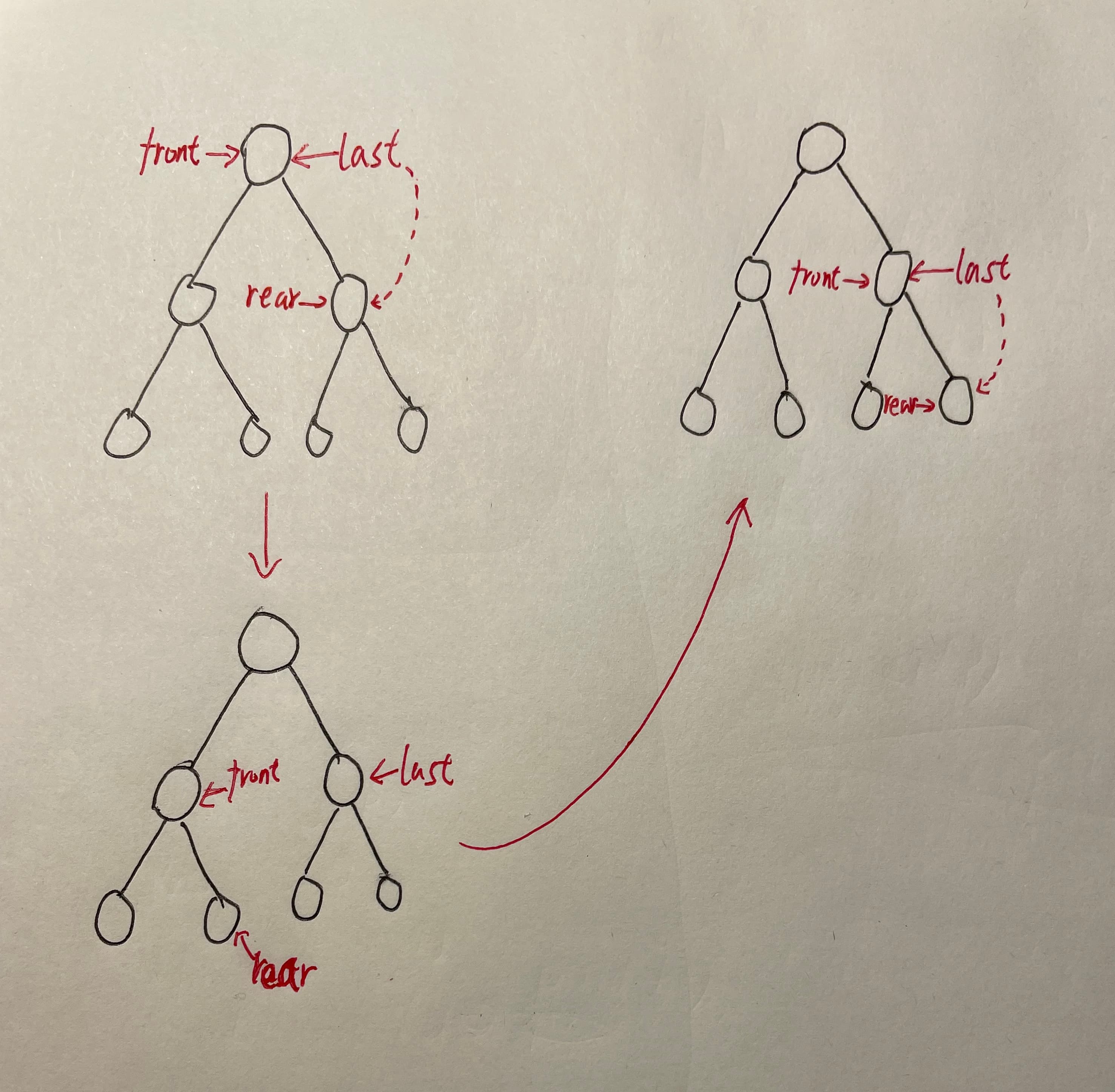
（注意front和rear本身直接表示的是队列中对头与队尾的元素，但是我们可以把它映射为二叉树中结点的位置）

计算二叉树某一结点的层数

例：计算指定结点*x所在的层次

递归实现

算法思想：在树的先序遍历中第一次遍历到该结点时指针是向下走的，第三次遍历到该结点指针向上走退回到该结点的父结点，所以让第一次遍历到时层数加1，第三次遍历到时层数减1

代码如下：

int h=1;
int fun(BiTree p,int x){
    if(p!=NULL){
        if(p->data==x)           //若找到则返回层数
            return h;
        ++h;                     //向下遍历层数加1
        fun(p->lchild,x);
        fun(p->rchild,x);
        --h;                     //向上返回层数减1
    }
}

非递归实现

算法思路：与求二叉树的高度算法类似，只不过在出入队的过程中判断是否为目标结点

int fun(BiTree T,BiTree x){
    int front=-1,rear=-1;   //初始化队列中的参数
    int level=1,last=0;     //初始化树的层数和last标记(初始根结点层数为1)
    BiTree Q[Maxsize];      //设置队列，因为要存放的元素是树的结点所以用BiTree来定义
    Q[++rear]=T;            //先让根节点入队
    BiTree p;               //用一个p指针来遍历二叉树
    while(front<rear){      //当队不空时循环
        p=Q[++front];                  //出队
        if(p==x)                       //若出队元素是x结点，则返回层数结束循环
            return level;
        if(p->lchild)                  //若有左孩子则左孩子入队
            Q[++rear]=p->lchild;
        if(p->rchild)                  //若有右孩子则右孩子入队
            Q[++rear]=p->rchild;
        if(front==last){               //若此次出队的结点是此层最后一个结点
            level++;                   //树的层数加1
            last=rear;                 //让last指向下一层的最后一个结点
        }
    } 
}

附 求结点在排序二叉树中的层次

求给定结点p在二叉排序树的层次

算法思想：由于排序二叉树的结点有明确的大小逻辑关系，所以不用像普通二叉树一样一次遍历整颗二叉树，只需判断待查找元素值与当前元素值来确定查找方向。

代码如下：

int level(BiTree bt,BiTree p){
    int n=0;                         //统计查找次数
    BiTree t=bt;
    if(bt!=NULL){
        n++;
        while(t->data!=p->data){
            if(p->data<t->data)      //在左子树查找
                t=t->lchild;
            else
                t=t->rchild;         //在右子树查找
            n++;                     //层次加1
        }
    }
    return n;
}

本篇随笔部分内容引用自B站UP主:计算机考研大师兄Day（48）_哔哩哔哩_bilibili