XMOJ 题目笔记
☆ 符号代表该比赛的订正已完成。
5 月 Div.2 ☆
场切:ABCDE
F 想出正解了,但是没写对拍 100->72,痛失 AK。
5 月 Div.1
场切:A(状压 DP)
B
TODO:
C
TODO:
D
简要题意:给定 \(n\)。你需要找一个数 \(w\),以 \(w\) 为参数画格子:在前 \(\lfloor \frac n w \rfloor\) 行每行画 \(w\) 个格子;紧接下来的一行画 \(n \bmod w\) 个格子紧贴左侧;以从上往下为第一关键字,从左往右为第二关键字,依次在格子中写上 \(1 \sim n\) 的数字。(下方有图解释)从 \(1\) 开始走,可以走到相邻(四连通)格子,不能走到质数格,目标为走到 \(n\)。找一个最小的 \(w\),使得目标被满足。保证 \(n\) 不为质数。可以证明答案必然存在。\(n \le 10^{24}\)。
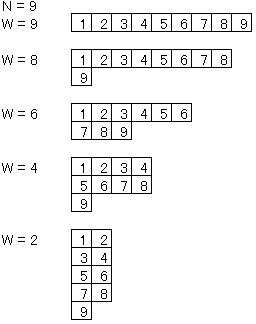
先写 BFS 暴力,观察可得,数据较小时无规律,数据较大时答案好像只有 \(8\) 和 \(14\)。
接下来不难了啊,我怎么就把这题给弃了呢!但凡仔细分析一下可知,\(n\) 足够大时,\(n \bmod 8 = 1\) 且 \(n-8\) 为质数时答案为 \(14\),否则答案为 \(8\)。
MR 判质数即可。(根据 OEIS A014233,\(10^{24}\) 范围内确定性判素可以用前 \(13\) 个质数)
6 月 Div.1
场切:A(环上 DP)
B
没想出正解,但是骗分骗到 48,非常好。
TODO:
C 跳房子游戏
想出正解了,但是 100->10。
简要题意:求 \(x\) 是数列 A010062(递推式:\(a_1 = 1, a_i = a_{i-1} + \text{popcount}(a_{i-1})\))的第几项(或报告 \(x\) 不在该数列中)。\(x \le 10^{12}\)。
TODO:
D 背景墙
简要题意:已知 \(n,m,k\),求用 \(k\) 种不同颜色给 \(n \times m\) 的方格染色本质不同的方案数(\(\bmod 10^9 + 7\))。两种方案本质不同,当且仅当两种方案不能通过上下左右的循环移位得到。\(n,m,k \le 10^9\)。
前置知识:Burnside 引理。
令 \((a,b)\) 表示向右移 \(a\) 位,向下移 \(b\) 位的置换。
根据 Burnside 引理,可知答案为 \(\frac 1 {nm} \sum\limits_{(a,b)} \left( (a,b) \text{下的置换不变元个数} \right)\)。
\((a,b)\) 作用下的轨道长均相同,为 \(L = \text{lcm}(\frac n {\gcd(a,n)}, \frac m {\gcd(b,m)})\)。轨道个数为 \(\frac {nm} L\)。
对于置换不变元,同一根轨道上必须染同样颜色,每根轨道的染色方案互相独立,置换不变元个数为 \(k^{\frac {nm} L}\)。
指数太抽象,所以幂运算用 \(\text{pow}\) 代替。
实现精细一点,分解质因数顺便把 \(\varphi\) 处理好,复杂度 \(O(d(n)d(m)(\log n + \log m))\)。
7 月 TG Day 1 图论 ☆
切 BCDEF。
A 最短路
XMOJ3353 是 BZOJ 原题。
简要题意:给定图,求 \(1 \to n\) 最短路。\(n \le 10^6, m \le 10^7\)。每个数据中有部分为随机生成。空间 256MB。
用 vector 存图会爆空间,需要用链式前向星。
直接二叉堆优化 Dijkstra 可过(\(O(m \log m)\) 为什么能过啊喂)。用 pbds 配对堆会 MLE。
卡常数:dis[n] 被求出之后直接退出 Dijkstra。
7 月 TG Day 2 膜你赛
一道都没场切。A 其实是会的,但是懒得写高精度。
A 是 NOIP 2006 原题,直接贴洛谷链接:P1066 [NOIP2006 提高组] 2^k进制数。场上懒得写高精度,用 int128 得 80pts。这样的策略事后证明是对的,我赛后高精度调了半天。
B
是 USACO 原题,直接贴洛谷链接:P3047 [USACO12FEB] Nearby Cows G
TODO:
C
TODO:
D
是 USACO 原题,直接贴洛谷链接:P1848 [USACO12OPEN] Bookshelf G
TODO:
7 月 TG Day 3 数据结构
切 ABCE。
TODO:
7 月 TG Day 4 膜你赛 ☆
个人评价:T1 绿、T2 绿、T3 黄、T4 黄。
场切:A(种类并查集)
C(二分)6e5 2log 被卡常 100->80,非常生气。
D(树状数组)场上写对忘交了 100->15,很傻逼。
B 幸福的道路
简要题意:给定一棵 \(n\) 个节点的树,边权非负。完成两个任务:(1)对于每个点 \(i\),求出以 \(i\) 为端点的最长树链长 \(D_i\)。(2)求出 \(D\) 中最大值减最小值 \(\le m\) 的最长区间,输出这个最长区间的长度。\(n \le 10^6\)
任务(1)的做法:两次 DFS 找到任意一条直径 \(AB\),可以证明 \(D_i = \max(\text{dis}(A,i), \text{dis}(B,i))\)。时间复杂度 \(\Theta(n)\)。
任务(2)的做法:显然可以双指针,为了在双指针的同时维护区间内的最值,用两个单调队列。时间复杂度 \(\Theta(n)\)。
7 月 TG Day 5 树上问题
个人评价:T1 蓝 / 紫、T2 绿、T3 蓝 / 紫、T4 黄。
切 BD。
A 异象石
几乎是 SDOI 原题(只是答案要除以 \(2\)),直接贴洛谷链接:P3320 [SDOI2015] 寻宝游戏 & CF176E Archaeology
观察到,设当前点集按 DFS 序排序后为 \(\{P_1, P_2, \cdots, P_m\}\),则当前的答案为 \(\frac 1 2 \sum\limits_{i=1}^m \text{dis}(P_i, P_{i \bmod m + 1})\)。加入和删除用平衡树维护即可。
B 逃学的小孩(这题切了)
场上猜结论猜对了(喜)。
是 NOI 2003 原题,直接贴洛谷链接:P4408 [NOI2003] 逃学的小孩
TODO:
C 树网的核
场上猜结论猜到只要任选一条直径了(喜)。
是 NOIP 2007 原题,直接贴洛谷链接:P1099 [NOIP2007 提高组] 树网的核
TODO:
*E 货车运输
是 NOIP 2013 原题,直接贴洛谷链接:P1967 [NOIP2013 提高组] 货车运输
TODO:
7 月 TG Day 6 膜你赛 ☆
个人评价:T1 橙 / 黄、T2 绿、T3 蓝、T4 绿。
场切 ACD。
B 数组开小了 1,改完就过了,编辑距离为 2,非常生气。
7 月 TG Day 7 DP
个人评价:T1 黄、T2 橙、T3 橙、T4 绿、T5 黄、T6 绿、T7 紫。
切 ABCEF。
D 决斗
简要题意:TODO:。\(n \le 300\)
环上 DP,断环成链,把链延长成原来的两倍。
设 \(f_{l,r}\) 为 \(l,r\) 两人是否能够把中间所有人干掉(为 \(0\) 或 \(1\))。可以 \(O(n^3)\) 分类讨论转移。
\(i\) 能存活到最后,当且仅当 \(f_{i,i+n} = 1\)。
*G 邮局
是 IOI 2000 原题,直接贴洛谷链接:P4767 [IOI2000] 邮局 加强版
TODO:
7 月 TG Day 8 膜你赛
个人评价:T1 绿、T2 绿、T3 绿、T4 绿 / 蓝。
场切 AD。
A(这题切了)
简要题意:给定 \(n,m\)(\(n \le 10^7, m \le 10^{14}\)),求:
\(n \le 10^7\),所以可以枚举 \(i\)。问题变为求 \(\left(\sum\limits_{j=1}^m d(i \times j)\right) \bmod 2\)。注意到 \(d(x) \bmod 2 = 1\) 当且仅当 \(x\) 为完全平方数,设 \(i\) 可表示为 \(f_i \times a^2\) 其中 \(f_i\) 不含平方因子,有:
\(f_i\) 可线性筛预处理。时间复杂度 \(\Theta(n)\)。
B
TODO:
C
KE 哥哥评价为唐题。
TODO:
7 月 TG Day 9 强连通分量
切 AB。
C 中队长
唐。
*D 最大半连通子图
7 月 TG Day 10 膜你赛
个人评价:T1 绿、T2 绿、T3 蓝、T4 绿。
场切 AB。
A 鼎纹(这题切了)
是原题,直接贴洛谷链接:P3585 [POI2015] PIE
简要题意:给定一个 \(n \times m\) 的图案 \(A\)(为一个 \(01\) 矩阵,\(1\) 表示黑块,\(0\) 表示透明)和一个 \(a \times b\) 的图案 \(B\)(同上),求:是否能用若干个图案 \(B\) 叠在一起(不允许旋转和翻面;不允许有格子叠了多个黑块,即所有的图案 \(B\) 的黑块不能重叠)。\(n,m,a,b \le 10^3\)。
好题。
TODO:
B 千帆渡(这题切了)
TODO:
C 旷野大计算
TODO:
D 线性规划问题
TODO:
7 月 TG Day 11 割点割边 ☆
切 ABCDE。
懒得评,题目不好。
7 月 TG Day 12 膜你赛
场切 ABC。
TODO:
A
B
7 月 TG Day 13 哈希/ST表
个人评价:T1 黄 / 绿、T2 绿、T3 蓝 / 紫、T4 紫。
切 AB。
B 是原题,直接贴洛谷链接:P3501 [POI2010] ANT-Antisymmetry & SP15569 STC02 - Antisymmetry
C 好点对
TODO:
\(f_i\) 是 \(i\) 为左端点的方案数,\(g_i\) 是 \(i\) 为右端点的方案数,用单调栈可以 \(O(n)\) 求。
对于每个询问,ST 表求出最大值的下标 \(p\),\(\sum\limits_{i=L}^{p-1} f_i + \sum\limits_{i=p+1}^{R} g_i\) 即为答案。
D 超级钢琴
是 NOI 2010 原题,直接贴洛谷链接:P2048 [NOI2010] 超级钢琴
TODO:
7 月 TG Day 14 膜你赛
个人评价:T1 绿、T2 绿、T3 蓝 / 紫、T4 蓝。
场切 D。
A 最长公共子序列
简要题意:给定一个长为 \(n\) 的数组 \(a\) 和一个长为 \(m\) 的数组 \(b\)。保证 \(a\) 中元素互不相同,\(b\) 中元素互不相同,但是 \(a\) 和 \(b\) 的元素可能有重复。求 \(a\) 与 \(b\) 的最长公共子序列(即 LCS)大小。\(n,m \le 3 \times 10^5\),值域 \(10^9\)。
朴素 DP 是没有前途的!因为朴素 DP 无法考虑到互不相同的特殊性质,即问题变为了朴素 LCS,据说可以归约到 OV 所以复杂度不可能再往下降了。可以优化到 \(O(\frac {nm} w)\),有模板题 LibreOJ6564,然而不足以通过本题。
不妨设 \(a\) 和 \(b\) 有 \(t\) 个公共元素,那么问题变为了两个长度为 \(t\) 的排列的 LCS。抄洛谷模板 P1439 【模板】最长公共子序列 即可。时间复杂度 \(O(n \log n)\)。
【重要部分】对拍
在场上做这题时,我的对拍犯了一个严重的错误,这是我的数据生成器:
mt19937 Rand(time(0));
void RandA(int n) {
uset<int> A;
uniform_int_distribution<int> dist(1, 1e9);
rep(i, 1, n) {
int a = dist(Rand);
while (A.find(a) != A.end())
a = dist(Rand);
A.insert(a);
cout << a << " \n"[i == n];
}
}
int main() { ios::sync_with_stdio(0); cin.tie(0);
int n = RandLR(1, 3000), m = RandLR(1, 3000);
cout << n << " " << m << endl;
RandA(n), RandA(m);
return 0;
}
这样随出来的 \(a\) 和 \(b\) 的 LCS 几乎永远是 \(0\),对拍永远能过,因此我在场上没有发现自己代码的问题,100->30。
B 训练
简要题意:你希望在 \(m\) 单位时间(即 \([0, m-1]\) 的区间)里获得尽量多的经验值。有 \(n\) 个物品,在第 \(x\) 单位时间使用第 \(i\) 个物品会消耗 \(c_i\) 单位时间(即时间变为 \(x+c_i\))获得 \(a_i - b_i (x + c_i)\) 的经验值。每个物品只能最多使用一次。\(n \le 10^3\),\(m \le 3 \times 10^3\),\(a_i \le 10^6\)。保证 \(a_i - b_i (x + c_i)\) 在任何时刻都不为负数。多测,\(5\) 组数据。
邻项交换贪心。
若 \(i\) 在前 \(j\) 在后,则贡献为 \(a_i - b_i (x_0 + c_i) + a_j - b_j (x_0 + c_i + c_j)\)。
若 \(j\) 在前 \(i\) 在后,则贡献为 \(a_j - b_j (x_0 + c_j) + a_i - b_i (x_0 + c_j + c_i)\)。
不妨设 \(i\) 在前 \(j\) 在后,相减得 \(- b_j c_i > - b_i c_j\),即 \(\frac {b_i} {c_i} > \frac {b_j} {c_j}\)。
排序后类似 01 背包 DP 即可。\(O(nm)\)。
C 鱼
XMOJ4714 懒得写简要题意。
TODO:
D 计树(这题切了)
是 HNOI 2004 原题,直接贴洛谷链接:P2290 [HNOI2004] 树的计数
简要题意:一棵 \(n\) 个节点的树,已知第 \(i\) 个节点的度数为 \(d_i\),求总共有几棵满足要求的树。保证答案不超过 \(10^{17}\)。\(n \le 150\)。
根据 Prufer 序列可得答案为 \(\frac {(n-2)!} {\prod\limits_{i=1}^n (d_i - 1)!}\)。
- 法 1:高精度计算即可。
- 法 2:计算分子分母中每个质因子出现次数。
- 法 3:把答案对一个大于 \(10^{17}\) 次方的质数取模,除法可以使用逆元。需要用
__int128。 - 法 4:根据多重组合数公式推导过程,答案可写为 \(\prod\limits_{i=1}^n \binom {\sum\limits_{j=1}^i (d_j - 1)} {d_i - 1}\),使用杨辉三角预处理组合数即可。
7 月 TG Day 15 真题
洛谷评价:T1 蓝、T2 绿、T3 蓝、T4 蓝。
A 以前做过,直接抄了。
B 时间复杂度错误的做法洛谷上过去了,XMOJ 机子太慢没卡过去。。。
A
是 CSP-S 2021 原题,直接贴洛谷链接:P7914 [CSP-S 2021] 括号序列
TODO:
B
是 CSP-S 2019 原题,直接贴洛谷链接:P5658 [CSP-S2019] 括号树
TODO:
C
是 CSP-S 2019 原题,直接贴洛谷链接:P5664 [CSP-S2019] Emiya 家今天的饭
TODO:
D
是 NOIP 2018 原题,直接贴洛谷链接:P5021 [NOIP2018 提高组] 赛道修建
TODO:

 浙公网安备 33010602011771号
浙公网安备 33010602011771号