AoPS - Chapter 3 More Triangles

本章主要讲解正弦定理、余弦定理、海伦公式、Stewart's Theorem。

本文在没有特殊说明时，默认在 \(\triangle ABC\) 中：

• \(a\) 为角 \(A\) 对边，\(b\) 为角 \(B\) 对边，\(c\) 为角 \(C\) 对边。
• \(r\) 为内切圆半径（inradius），\(R\) 为外接圆半径（circumradius）。
• \([ABC]\) 为 \(\triangle ABC\) 的面积。
• \(s\) 为半周长（semiperimeter）。

余弦定理（law of cosines）

书上给了一个运用圆幂定理（the Power of a Point Theorem）的方法，但是太过复杂，事实上直接解三角形即可证。

\[c^2 = a^2 + b^2 - 2ab \cos C \]

\[\cos C = \dfrac {a^2 + b^2 - c^2} {2ab} \]

一般用于：

• 已知 SAS 求 S
• 已知 SSS 求 A

经典结论

• \(c^2 < a^2 + b^2\) 当且仅当 \(\angle C\) 为锐角（acute angle）
• \(c^2 > a^2 + b^2\) 当且仅当 \(\angle C\) 为钝角（obtuse angle）

正弦定理（law of sines）

\[\dfrac a {\sin A} = \dfrac b {\sin B} = \dfrac c {\sin C} = 2R \]

一般用于：

• 已知 ASA / AAS 求 S
• 已知 SAS / SSA 求 A

经典结论

小角对小边，大角对大边。（\(\angle_A > \angle_B\) 当且仅当 \(a > b\)）

正切定理（law of tangents）

\[\dfrac {a-b} {a+b} = \dfrac {\tan \frac {A-B} 2} {\tan \frac {A+B} 2} \]

三角形的面积公式

\[[ABC] = \dfrac 1 2 ab \sin C = \dfrac {abc} {4R} = rs = \dfrac {a^2 \sin B \sin C} {2 \sin A} = 2R^2 \sin A \sin B \sin C \]

海伦公式（Heron's formula）

\[[ABC] = \sqrt {s(s-a)(s-b)(s-c)} \]

展开形式：

\[[ABC] = \dfrac 1 4 \sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+b-c)} \]

Stewart's Theorem

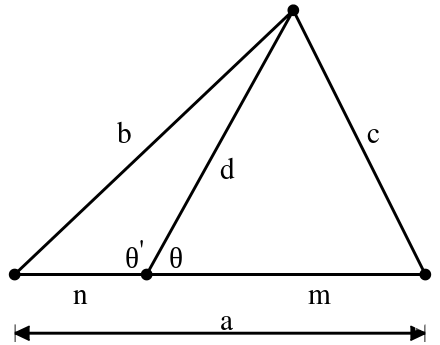
\[man + dad = bmb + cnc \]

（A \(man\) and his \(dad\) put a \(bomb\) in the \(sink\)）

中线长公式

当 \(m=n\) 时：

\[d = \sqrt {\dfrac 1 2 b^2 + \dfrac 1 2 c^2 - \dfrac 1 4 a^2} \]

角平分线长公式

当 \(\dfrac b n = \dfrac c m\) 时：

\[d = \sqrt {bc \left(1 - \dfrac {a^2} {(b+c)^2}\right)} \]

另一个公式：（习题 No. 53）

\[d = 2 \cos \frac A 2 \dfrac 1 {\frac 1 b + \frac 1 c} \]

课后习题

No. 46

Problem

Show that in \(\triangle ABC\),

\[\sin \dfrac A 2 = \sqrt {\dfrac {(s-b)(s-c)} {bc}} \]

Solution

\[\begin{aligned} RHS &= \sqrt {\dfrac {\frac {a-b+c} 2 \frac {a+b-c} 2} {bc}} \\ &= \dfrac 1 2 \sqrt {\dfrac {a^2 -b^2 - c^2 + 2bc} {bc}} \\ &= \dfrac 1 2 \sqrt{2 - 2 \cos A} \\ &= \dfrac 1 2 \sqrt {2 - 2 \left(\cos^2 \frac A 2 - \sin^2 \frac A 2\right)} \\ &= \dfrac 1 2 \sqrt {4 \sin^2 \frac A 2} \\ &= \sin \frac A 2 \end{aligned}\]

\(\square\)

No. 57

Problem

Prove that if \(\alpha, \beta, \gamma > 0\) and \(\alpha + \beta + \gamma = \pi\), then \(\sin 2\alpha + \sin 2\beta + \sin 2\gamma = 4 \sin\alpha \sin\beta \sin\gamma\).

Solution

令 \(\alpha, \beta, \gamma\) 为一个三角形的三个角，记为 \(A,B,C\)。

\[\begin{aligned} RHS &= 4 \sin A \sin B \sin C \\ &= 4 \dfrac {abc} {8R^3} \\ &= \dfrac 2 {R^2} [ABC] \end{aligned}\]

\[\begin{aligned} LHS &= \sin 2A + \sin 2B + \sin 2C \\ &= 2 (\sin A \cos A + \sin B \cos B + \sin C \cos C) \\ &= \dfrac 2 {R^2} [ABC] \end{aligned}\]

LHS 的最后一步可以通过圆周角定理之后作高得出。\(\square\)