笔记·简单矩阵

笔记·简单矩阵

方阵

行数等于列数的矩阵称为方阵。方阵是一种特殊的矩阵。对于「\(n\) 阶矩阵」的习惯表述，实际上讲的是 \(n\) 阶方阵。阶数相同的方阵为同型矩阵。

主对角线

对于矩阵 \(A\)，主对角线是指 \(A_{i,i}\) 的元素。

单位矩阵 \(I\)

一般用 \(I\) 来表示单位矩阵，单位矩阵的主对角线上的元素为 \(1\)，其余为 \(0\)。

一个矩阵乘上一个大小合适的单位矩阵等于它本身。

矩阵乘法

两个矩阵 \(A,B\)，其中，矩阵 \(A\) 是 \(P\times M\) 的，矩阵 \(B\) 是 \(M\times Q\) 的。

设矩阵 \(C=A\times B\)，那么 \(C\) 就是 \(P\times Q\) 的，而且

\[C_{i,j}=\sum_{k=1}^M A_{i,k}\times B_{k,j} \]

代码

node cheng(node a,node b){
	node ans;
	for(int i=0;i<=siz;i++){
		for(int j=0;j<=siz;j++){
			for(int k=0;k<=siz;k++){
				ans.a[i][j]+=a.a[i][k]*b.a[k][j];
				ans.a[i][j]%=mod;
			}
		}
	}
	return ans;
}

矩阵快速幂

矩阵乘法是满足结合律的。

类比普通快速幂即可。

node ksm(node a,int b){
	node ans;
	for(int i=0;i<=siz;i++)ans.a[i][i]=1;
	for(;b;b>>=1){
		if(b&1)ans=cheng(ans,a);
		a=cheng(a,a);
	}
	return ans;
}

矩阵加速递推

斐波那契数列

做法

递推式子我们都知道：

\[f_i= \begin{cases} 1 & i\le 2\\ f_{i-1}+f_{i-2} & i>2\\ \end{cases} \]

容易在线性时间内求出这个玩意。

然后我们来求求 \(f_{10^{18}}\)。

容易发现，线性太慢了。然后考虑矩阵加速递推。

首先我们把他转换成一项推出另一项的样子。

那不如吧斐波那契的两项放一块，成 \(\left[ \begin{array}{c}f_i & f_{i-1} \end{array}\right]\) 的样子。

然后不妨设 \(F_i=\left[ \begin{array}{c}f_i & f_{i-1} \end{array}\right]\)。

然后我们考虑求一个矩阵 \(base\)，使得 \(F_{i-1}\times base\) 的顶上两项是 \(\left[ \begin{array}{c}f_i & f_{i-1} \end{array}\right]\)。

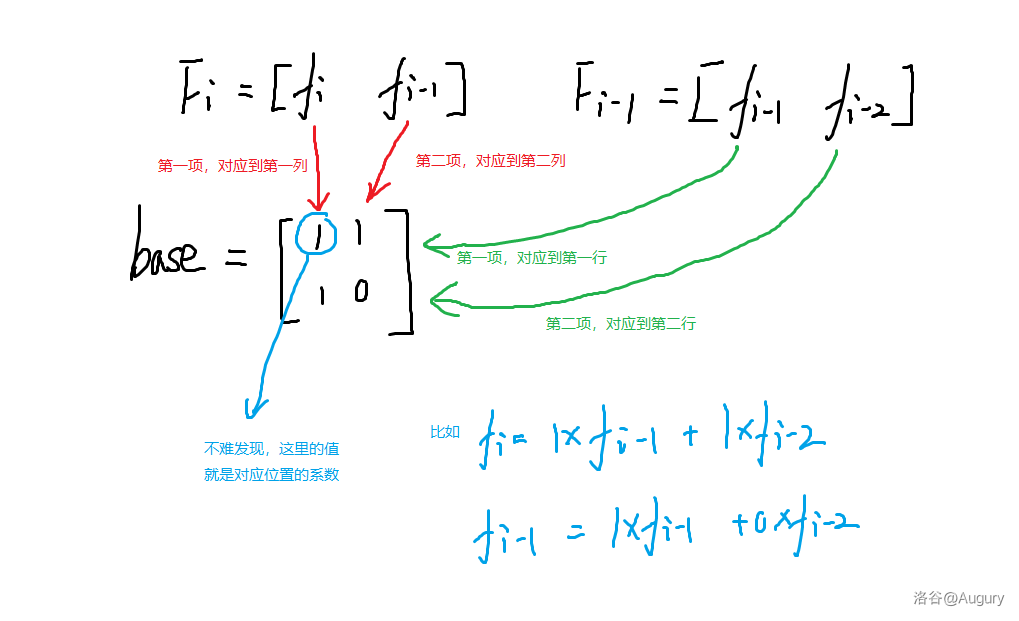
于是：

\[base= \begin{bmatrix} 1 & 1\\ 1 & 0 \end{bmatrix} \]

然后用矩阵快速幂直接冲就行了。。。

代码

signed main(){//那就……只放主函数吧！
	n=read();
	if(n<=2){
		puts("1");
		return 0;
	}
	ans.a[1][1]=ans.a[1][2]=1;//初始化斐波那契的前两项
	base.a[1][1]=base.a[1][2]=base.a[2][1]=1;//初始化base数组
	base=ksm(base,n-2);//因为已经求出了前两项，所以是n-2次方
	ans=cheng(ans,base);
	cout<<ans.a[1][1];
	return 0;
}

广义斐波那契数列

题意

广义的斐波那契数列是指形如 \(a_n=p\times a_{n-1}+q\times a_{n-2}\) 的数列。
今给定数列的两系数 \(p\) 和 \(q\)，以及数列的最前两项 \(a_1\) 和$ a_2$，另给出两个整数 \(n\) 和 \(m\)，试求数列的第 \(n\) 项 \(a_n \bmod m\)。

做法

和上面那个普通斐波那契数列没啥区别，改一下值就行了。

然后矩阵就是：

\[base= \begin{bmatrix} p & 1\\ q & 0 \end{bmatrix} \]

直接跑即可。

代码

signed main(){//只放主函数吧
	p=read(),q=read(),a1=read(),a2=read(),n=read(),mod=read();
	if(n<=2){
		if(n==1)cout<<a1;
		else cout<<a2;
		return 0;
	}
	ans.a[1][1]=a2;//恶臭初始化
	ans.a[1][2]=a1;
	base.a[1][2]=1;
	base.a[1][1]=p;
	base.a[2][1]=q;
	base=ksm(base,n-2);
	ans=cheng(ans,base);
	cout<<ans.a[1][1];
	return 0;
}

【模板】矩阵加速（数列）

题意

已知一个数列 \(a\)，它满足：

\[a_x= \begin{cases} 1 & x \in\{1,2,3\}\\ a_{x-1}+a_{x-3} & x \geq 4 \end{cases} \]

求 \(a\) 数列的第 \(n\) 项对 \(10^9+7\) 取余的值。

做法

类比上面，找系数，QwQ。

然后矩阵就是：

\[base= \begin{bmatrix} 1 & 1 & 0\\ 0 & 0 & 1\\ 1 & 0 & 0 \end{bmatrix} \]

直接跑即可。

这不是三倍经验吗

代码

void real_main(){//啊哈哈多组数据
	base.clear();
	ans.clear();
	cin>>n;
	if(n<=3){
		cout<<1<<'\n';
		return;
	}
	base.a[1][1]=base.a[1][2]=base.a[3][1]=base.a[2][3]=1;//初始化
	ans.a[1][1]=ans.a[1][2]=ans.a[1][3]=1;
	base=ksm(base,n-3);
	ans=cheng(ans,base);
	cout<<ans.a[1][1]<<'\n';
}
signed main(){
	int T=read();
	while(T--)real_main();
}

Darth Vader and Tree

题意

有一个无限大的有根树，树上的每一个节点都有 \(n\) 个子节点（\(1 \leq n \leq 10^5\)），任意一个节点它的第 \(i\) 个子节点之间的距离为 \(d_i\)（\(1 \leq d_i \leq 100\)）。

给出一个数 \(x\)（\(0 \leq x \leq 10^9\)），求有多少个节点到根节点的距离小于等于 \(x\)，输出答案对 \(10^9+7\) 取模后的结果。

做法

首先，当 \(x=0\) 时，输出 \(0\)。

其次，当 \(x=1\) 时，统计 \(1\) 的个数。

然后，然后就不会了/kk

然后向机房大佬询问 \(dp\) 式子：

\[dp_i= \begin{cases} 1 & i=0\\ \sum_{k=1}^n[d_k\le i]dp_{i-d_k} & i>0 \end{cases} \]

首先，从 \(1\) 到 \(n\) 枚举太慢了，而 \(d_i\) 的值域又非常小，所以考虑开一个桶来记录每个 \(d_i\) 出现了多少次。

不妨设 \(t_i=\sum_{k=1}^n[d_k=i]\)。

然后我们改进了这个 \(dp\) 式子！

\[dp_i= \begin{cases} 1 & i=0\\ \sum_{k=1}^{100}[k\le i]dp_{i-k}\times t_{k} & i>0 \end{cases} \]

然后，我们就会了 \(x\le 10^5\) 的情况。

发现这个时候要求出 \(dp_i\) 只需要 \(100\) 项 \(dp\) 值！然后考虑矩阵加速递推。

我们要求 \(sum_i=\sum_{k=1}^i dp_i\)。

那么不妨将 \(sum_i\) 加入矩阵。

那么我们每个矩阵就是：

\[\begin{bmatrix} sum_i & dp_i & dp_{i-1} & dp_{i-2} & \cdots & dp_{100} \end{bmatrix} \]

考虑转移矩阵 \(base\)，直接按照上面的来就行。

但是要求 \(sum_i\) 啊！我们已知了 \(sum_{i-1}\)，又能算出 \(dp_i\)，那么直接把这俩加起来得了。

所以：

\[base= \begin{bmatrix} 1 & 0 & 0 & 0 & \cdots & 0\\ t_1 & t_1 & 1 & 0 & \cdots & 0\\ t_2 & t_2 & 0 & 1 & \cdots & 0\\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ t_{99} & t_{99} & 0 & 0 &\cdots & 1\\ t_{100} & t_{100} & 0 & 0 &\cdots & 0 \end{bmatrix} \]

然后跑。

代码

void init(){
	for(int i=1;i<=n;i++)++t[d[i]];
	sum[0]=a[0]=1;
	for(int i=1;i<=siz;i++)for(int j=1;j<=i;j++)a[i]+=(a[i-j]*t[j])%mod,a[i]%=mod;
	for(int i=1;i<=siz;i++)sum[i]=(sum[i-1]+a[i])%mod;
}
signed main(){
	n=read(),m=read();
	for(int i=1;i<=n;i++)d[i]=read();
	init();
	if(m<=siz)return cout<<sum[m],0;

	base.a[0][0]=1;
	for(int i=1;i<=siz;i++)base.a[i][0]=base.a[i][1]=t[i];
	for(int i=2;i<=siz;i++)base.a[i-1][i]=1;

	ans.a[0][0]=sum[siz];
	for(int i=1;i<=siz;i++)ans.a[0][siz-i+1]=a[i];

	base=ksm(base,m-100);
	ans=cheng(ans,base);

	cout<<ans.a[0][0];
	return 0;
}

[TJOI2017]可乐和它的加强版

题意

加里敦星球的人们特别喜欢喝可乐。因而，他们的敌对星球研发出了一个可乐机器人，并且放在了加里敦星球的 \(1\) 号城市上。这个可乐机器人有三种行为： 停在原地，去下一个相邻的城市，自爆。它每一秒都会随机触发一种行为。现在给加里敦星球城市图，在第 \(0\) 秒时可乐机器人在 \(1\) 号城市，问经过了 \(t\) 秒，可乐机器人的行为方案数是多少？

\(n,m\le 100\)，原版 \(t\le 10^6\)，加强版 \(t\le10^9\)。

做法

首先，考虑暴力 \(dp\)。

发现自爆操作不好搞。

发现这个东西就相当于走到一个虚节点（比如 \(0\) 号），然后不能再出来。从所有点向 \(0\) 号节点连单项边即可。

记 \(dp_{i,j}\) 表示在第 \(i\) 时刻，在 \(j\) 号点的方案数。

所以：

\[dp_{i,j} = \begin{cases} 1 & i = 0,j = 1\\ 0 & i = 0,j\ne 1\\ dp_{i-1,j}+\sum[(k,j)\in E]dp_{i-1,k} & i\ge 1 \end{cases} \]

这样直接暴力 \(dp\) 可以得到原版题的 \(100\) 分和加强版的 \(50\) 分，肥肠强大。

不难发现，这个东西是可以矩阵加速的。

设 \(D_i=\begin{bmatrix} dp_{i,0} & dp_{i,1} & dp_{i,2} & \cdots & dp_{i,n}\end{bmatrix}\)，然后考虑用 \(D_{i-1}\) 算出 \(D_i\)。

根据上面的 \(dp\) 式子，容易得到 \(base\) 矩阵：

\[base=\begin{bmatrix} 1 & [(j,i\in E)] & [(j,i\in E)] & \cdots & [(j,i\in E)]\\ 1 & 1 & [(j,i\in E)] & \cdots & [(j,i\in E)]\\ 1 & [(j,i\in E)] & 1 & \cdots & [(j,i\in E)]\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & [(j,i\in E)] & [(j,i\in E)] &\cdots & 1 \end{bmatrix} \]

呃呃呃也不知道艾弗森括号能不能在这里用/kk。\(i,j\) 分别表示行和列。

初始状态就是：

\[\begin{bmatrix} 0 & 1 & 0 & 0 & \cdots & 0 \end{bmatrix} \]

然后直接跑即可。

代码

int main(){
	n=read(),m=read();
	for(int i=1,u,v;i<=m;i++){
		u=read(),v=read();
		base.a[u][v]=base.a[v][u]=1;//加边，双向边
	}
	t=read();
	for(int i=0;i<=n;i++)base.a[i][i]=1,base.a[i][0]=1;//初始化
	ans.a[0][1]=1;
	base=ksm(base,t);
	ans=cheng(ans,base);
	for(int i=0;i<=n;i++)sum=(sum+ans.a[0][i])%mod;
	cout<<sum;//得到答案
	return 0;
}

[NOI Online #1 入门组] 魔法

必须用魔法打败魔法！

题意

\(n\) 做城市，\(m\) 条道路，道路有费用。你要从 \(1\) 走到 \(n\)。

神奇的是，你能使用魔法让下一次经过的边权变成它的相反数。使用魔法只是改变一次的花费，而不改变一条道路自身的费用。

\(1 \leq n \leq 100,1 \leq m \leq 2500,0 \leq k \leq 10^6\)。

做法

首先，当 \(k\le 1000\) 时，直接分层图做即可。可以取得 \(90\) 分的好成绩。

当然，我们想要的是 \(100\) 分。

从分层图入手，设 \(dp_{i,j,k}\) 表示使用了最多 \(k\) 次魔法后，从 \(i\) 到 \(j\) 的最短路径长度。

然后考虑怎么求这个东西。

先考虑暴力 \(dp\) 怎么做。

首先，当 \(k=0\) 时，使用 \(\text{Floyd}\) 进行求解即可。然后就得到了 \(dp_{i,j,0}\)。

接下来，考虑 \(k=1\) 的情况。

我们发现，可以拿存在的边出来进行松驰，也就是：

\[dp_{i,j,i}=\min_{(u,v)\in E}dp_{i,u,i-1}+dp_{v,j,i-1}-w(u,v) \]

这样就有个问题：我这次可不可以不用魔法捏？当然是可以的。但是上面的式子也没有算啊？为啥不加一条 \((i,i,0)\) 的边用来糊弄一下捏？

首先，如果从 \(i\) 到 \(j\) 的路上如果有边没用过魔法，那肯定是要用的。

如果都用过了魔法，那我应该考虑绕个圈。如果绕个圈更优，我自然会再使用一次魔法。如果不是更优捏？那么，当 \((u,v)\) 在 \(i\) 到 \(j\) 的路径上时，我们这种更新方式不会对答案造成任何的影响。因为 \(dp\) 式子就相当于自动去掉这条边已经用的魔法，然后再使用一次魔法。

然后呢？矩阵加速？这玩应连个乘号都不带的，连个加号都不带的，咋矩阵加速？

呃呃呃，实际上不是矩阵加速，就是用了一下矩阵加速的思想。

容易发现，使用 \(100\) 次魔法就相当于使用 \(50\) 次魔法，再使用 \(50\) 次魔法。

也就是说，这个玩意是满足结合律的。那自然是使用快速幂（的思想）了！

问题来了：我咋一次性使用 \(50\) 次魔法捏？

容易发现，一次性使用 \(50\) 次魔法就相当于用 \(50\) 次魔法对图进行强化，然后再用这个图来对另一个使用过 \(50\) 次魔法的图进行更新。然后就可以得到使用 \(100\) 次魔法的效果。

也就是：

\[dp_{i,j,p+q}=\min_{k=1}^n dp_{i,k,p}+dp_{k,j,q} \]

容易发现，这个式子长得很像矩阵乘法，只是求和变成了去最小值，乘法变成了加法。

那么，只要证明我们的这个运算满足结合律就行了。

然后，感谢ChatGPT提供的理性证明/doge：

假设有三个矩阵 \(A\), \(B\), \(C\)。

首先将加法改成取最小值，乘法改为加法后的矩阵乘法表示为：

\[(A \otimes B)_{ij} = \min_k\{A_{ik}+B_{kj}\} \]

然后我们来证明 \((A\otimes B)\otimes C = A\otimes (B\otimes C)\)。

左边矩阵乘法：

\[[(A \otimes B)\otimes C]_{ij} = \min_k\{(A \otimes B)_{ik} + C_{kj}\} \]

代入定义式并展开：

\[\begin{aligned} [(A \otimes B)\otimes C]_{ij} &= \min_k\{\min_m\{A_{im}+B_{mk}\}+C_{kj}\} \\ &= \min_k\{\min_m\{A_{im}+B_{mk}+C_{kj}\}\} \end{aligned} \]

右边矩阵乘法：

\[[A\otimes(B \otimes C)]_{ij} = \min_k\{A_{ik} + (B \otimes C)_{kj}\} \]

代入定义式并展开：

\[\begin{aligned} [A\otimes(B \otimes C)]_{ij} &= \min_k\{A_{ik}+\min_m\{B_{km}+C_{mj}\}\} \\ &= \min_k\{\min_m\{A_{ik}+B_{km}+C_{mj}\}\} \end{aligned} \]

因此，左边矩阵乘法和右边矩阵乘法计算结果相同，证毕。

于是，它是对的。

代码

struct node{
	int a[maxn][maxn];
	node(){memset(a,0x3f,sizeof(a));}//呃呃呃这里初始化成inf
}base;
node cheng(node a,node b){//魔改版矩阵乘法
	node ans;
	for(int k=1;k<=n;k++)
		for(int i=1;i<=n;i++)
			for(int j=1;j<=n;j++)
				ans.a[i][j]=min(ans.a[i][j],a.a[i][k]+b.a[k][j]);
	return ans;
}
node ksm(node a,int b){
	node ans;
	for(int i=0;i<=n;i++)ans.a[i][i]=0;//在这里的单位矩阵对角线是0，其他是inf
	for(;b;b>>=1){
		if(b&1)ans=cheng(ans,a);
		a=cheng(a,a);
	}
	return ans;
}
int dis[maxn][maxn];
signed main(){
	memset(dis,0x3f,sizeof(dis));
	n=read(),m=read(),k=read();
	for(int i=1,u,v,w;i<=m;i++){
		u=read(),v=read(),w=read();
		e.push_back((edge){u,v,w});
		dis[u][v]=min(dis[u][v],w);
	}
	for(int k=1;k<=n;k++)
		for(int i=1;i<=n;i++)
			for(int j=1;j<=n;j++)dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);//量子Floyd
	for(int i=1;i<=n;i++)dis[i][i]=0;
	if(k==0)return cout<<dis[1][n],0;
	for(edge k:e)
		for(int i=1;i<=n;i++)
			for(int j=1;j<=n;j++)
				base.a[i][j]=min(base.a[i][j],min(dis[i][j],dis[i][k.u]+dis[k.v][j]-k.w));//处理出k=1的情况
	base=ksm(base,k);
	cout<<base.a[1][n];
	return 0;
}

更加强大的结论

如果外层和内层运算有分配和结合律之类的，那么这个矩阵乘法有结合律。

可以自己手推一下。

然后

因为它满足结合律，所以我们可以用快速幂（的思想，和代码）来进行优化。

然后，然后我们就能用它做更加离谱的加速了呀。

Flights for Regular Customers

题意

感谢ChatGPT提供的翻译~

在这个国家中，有 \(n\) 个城市，分别用从 \(1\) 到 \(n\) 的正整数编号。每个城市都有一个机场。

此外，有一家唯一的航空公司，他们有 \(m\) 条航线。不幸的是，如果你没有成为这家航空公司的常客，就无法使用这些航班。也就是说，只有当你之前至少乘坐了 \(d_i\) 次航班后，才能享受从城市 \(a_i\) 到城市 \(b_i\) 的第 \(i\) 次航班。

请注意，第 \(i\) 条航线恰好飞行从城市 \(a_i\) 到城市 \(b_i\) ，不能用于从城市 \(b_i\) 到城市 \(a_i\) 的飞行。有趣的是，可能会有具有美丽天空景色的娱乐性飞行，始发地和目的地是同一个城市。

你需要从城市 \(1\) 前往城市 \(n\) 。不幸的是，你从未乘坐过飞机。你至少需要乘坐多少次航班才能到达城市 \(n\)？

请注意，同一条航线可以多次使用。

这时洛谷的简化版题面：

给定一张 \(n\) 个点 \(m\) 条边的有向图。
一开始你在 \(1\) 号节点，你要走到 \(n\) 号节点去。
只有当你已经走过了至少 \(d_i\) 条边时，你才能走第 \(i\) 条边。
问最少要走多少条边，或判断无法到达。
\(n,m \le 150\)，\(d_i \le 10^9\)。

做法

首先，先问一个简单的问题：经过 \(k\) 条边能到达哪些点？

这个玩意直接 \(dp\) 即可。设 \(dp_{i,j}\) 表示经过 \(j\) 条边后，能不能到达 \(i\) 号点。那么转移就是：

\[dp_{i,j}=\begin{cases} 1& i=1,j=0\\ 0 & i\ne 1,j=0\\ \bigvee_{(k,i)\in E\wedge d(k,i)\le j}dp_{k,j-1} & j\ge 1 \end{cases} \]

容易发现，\(d\le10^9\)。所以直接暴力 \(dp\) 肯定是超时的。

考虑矩阵加速递推：把加法换成或，乘法换成与。

容易发现，随着 \(j\) 变大，有新的边会加入。这太烦了。我们要解决这个问题。我们要让他不变。

怎么让他不变呢？容易发现，\(d\) 最多只有 \(m\) 种，那么我们对于 \(d\) 值拆分就行了。

然后我们就能快乐地求出 \(dp_{i,j}\) 值啦~

求出这个玩意有啥用捏？我们可以顺便维护一下 \(n\) 号点有没有被经过过，也就是 \(\bigvee_{k=1}^j dp_{n,k}\)。

知道这个，就可以愉快地二分了。

复杂度捏？\(\Theta(n^3m\log_2^2d)\)，其中二分一个 \(\log\)，快速幂 \(n^3\log_2d\)，一共进行 \(m\) 次。

算出来数的话……\(150^3\times 150\times \log_2^210^9=150^4\times 30^2\approx 4.5\times 10^{11}\)，太棒了。

首先，我们的矩阵乘法就是与啊或啊什么的，于是考虑调整循环顺序，然后使用 bitset优化。

不妨从 \(\text{OI-wiki}\) 取一段代码：

// 以下文的参考代码为例
inline mat operator*(const mat& T) const {
  mat res;
  for (int i = 0; i < sz; ++i)
    for (int j = 0; j < sz; ++j)
      for (int k = 0; k < sz; ++k) {
        res.a[i][j] += mul(a[i][k], T.a[k][j]);
        res.a[i][j] %= MOD;
      }
  return res;
}

// 不如
inline mat operator*(const mat& T) const {
  mat res;
  int r;
  for (int i = 0; i < sz; ++i)
    for (int k = 0; k < sz; ++k) {
      r = a[i][k];
      for (int j = 0; j < sz; ++j)
        res.a[i][j] += T.a[k][j] * r, res.a[i][j] %= MOD;
    }
  return res;
}

这是普通的矩阵乘法，重新排列循环以提高空间局部性，会在得到常数级别的提升。

然后来考虑一下位运算。也就是：

//这段是自己写的了（
//把这个：
mat operator * (const mat &nxt)const{
	mat ans;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
	        for(int k=1;k<=n;k++)
                ans.val[i][j]|=val[i][k]&nxt.val[k][j];
    return ans;
}
//换成：
mat operator * (const mat &nxt)const{
	mat ans;
    for(int i=1;i<=n;i++)
        for(int k=1;k<=n;k++)
            if(val[i][k])
		        for(int j=1;j<=n;j++)
        	        ans.val[i][j]|=nxt.val[k][j];
    return ans;
}
//然后就可以bitset优化，把j循环去掉：
mat operator * (const mat &nxt)const{
    mat ans;
    for(int i=1;i<=n;i++)
        for(int k=1;k<=n;k++)
            if(val[i][k])
                ans.val[i]|=nxt.val[k];
    return ans;
}

这样复杂度就可以除上一个 \(w\) 了。

然后，当我们知道走 \(j\) 步可以到哪些点之后，我们就可以直接知道能否到达和最短路长度了。

我们从所有可到达的点开始，只经过小于等于当前 \(d\) 的边，跑 \(\text{bfs}\)，如果不能到达，就继续加长度，直到能到达或者所有边都可用。

然后，然后就做完了。复杂度 \(\Theta(\frac{n^3m\log_2d}{w})\)，可过。

代码

struct mat{
	bitset<maxn>val[maxn];
	bitset<maxn> & operator [] (const int pos){//方便起见，搞个bitset加速
		return val[pos];
	}
	mat operator * (const mat &nxt)const{//bitset加速矩阵乘法
		mat ans;
		for(int i=1;i<=n;i++){
			for(int k=1;k<=n;k++){
				if(val[i][k])
					ans.val[i]|=nxt.val[k];
			}
		}
		return ans;
	}
	void clear(){//清空
		for(int i=0;i<maxn;i++)val[i]=0;
		return;
	}
}base,op;
void bfs(int lim){//lim是限制，只能走d<=lim的边
	memset(dis,-1,sizeof(dis));
	for(int i=1;i<=n;i++)if(base[1][i]){
		q.push(i);
		dis[i]=0;
	}
	while(!q.empty()){
		int now=q.front();q.pop();
		for(edge nxt:g[now]){
			if(nxt.d>lim||~dis[nxt.v])continue;
			dis[nxt.v]=dis[now]+1;
			q.push(nxt.v);
		}
	}
}
int main(){
	n=read(),m=read();
	for(int i=1,u,v,d;i<=m;i++){
		u=read(),v=read(),d=read();
		e.push_back((edge){u,v,d});
		g[u].push_back((edge){u,v,d});
	}
	sort(e.begin(),e.end());
	for(edge i:e)mp.push_back(i.d);
	mp.erase(unique(mp.begin(),mp.end()),mp.end());
	for(edge i:e)li[lower_bound(mp.begin(),mp.end(),i.d)-mp.begin()].push_back(i);
	base[1][1]=1;//一开始只能走到1号点自己
	bfs(0);
	if(~dis[n]){//只能走0的边
		cout<<dis[n];
		exit(0);
	}
	for(int i=1;li[i].size();i++){
		op.clear();
		for(int k=0;k<i;k++)for(edge j:li[k])op[j.u][j.v]=1;//加入边
		op=ksm(op,mp[i]-mp[i-1]);//快速幂处理
		base=base*op;
		bfs(mp[i]);
		if(~dis[n]){
			cout<<dis[n]+mp[i];
			exit(0);
		}
	}
	puts("Impossible");
	return 0;
}

Power of Matrix

题意

你有一个 \(n\times n\) 矩阵 \(A\)，设 \(S_n=\sum_{k=1}^nA^k\)，求 \(S_k\)。

\(n\le 40,k\le 10^6\)。

做法

容易发现，这个东西不好做。

先来考虑一个简单的问题：你有一个数 \(a\)，求 \(\sum_{k=1}^na^k\)。

这个东西是有通项公式的，要用快速幂算，而且对矩阵不支持。

我们考虑使用矩阵加速递推。

我们设答案矩阵为：

\[ans=\begin{bmatrix} a^n & S_n \end{bmatrix} \]

那么显然转移矩阵为：

\[base=\begin{bmatrix} a & a\\ 0 & 1 \end{bmatrix} \]

然后考虑对矩阵使用这个东西，发现可行。于是：
我们设答案矩阵为：

\[ans=\begin{bmatrix} A^n & S_n \end{bmatrix} \]

那么显然转移矩阵为：

\[base=\begin{bmatrix} A & A\\ 0 & 1 \end{bmatrix} \]

然后矩阵快速幂即可。

容易发现，把这四个矩阵放在一块，成一个 \(2n\times 2n\) 的矩阵，得到的答案是一样的。这样常数会小很多，而且不用专门写个矩阵加法和矩阵套矩阵。

在这里放一下我的矩阵套矩阵吧/kk

代码

struct mat{
	struct matline{//矩阵的一行
		int val[maxn];
		matline(){memset(val,0,sizeof(val));}
		inline int & operator [] (const int pos){
			return val[pos];
		}
		inline void clear(){memset(val,0,sizeof(val));}
	}val[maxn];
	inline matline & operator [] (const int pos){//这样在下面用的时候会方便且美观一些
		return val[pos];
	}
	inline mat operator * (const mat &nxt)const{//矩阵乘法
		mat ans;
		for(int i=1;i<=(n<<1);i++){
			for(int k=1;k<=(n<<1);k++){
				int tmp=val[i].val[k];
				for(int j=1;j<=(n<<1);j++){
					ans.val[i].val[j]=(ans.val[i].val[j]+(tmp*nxt.val[k].val[j]))%mod;
				}
			}
		}
		return ans;
	}
	inline void clear(){for(int i=0;i<=n;i++)val[i].clear();}
};
inline bool real_main(){//多组数据啊哈哈
	a.clear();
	ans.clear();
	base.clear();
	n=read(),m=read();
	if(!n)return 0;
	for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)a[i][j]=(read())%mod;
	for(int i=1;i<=n;i++)for(int j=1;j<=n;j++){
		base[i][j]=base[i][j+n]=ans[i][j]=ans[i][j+n]=a[i][j];//矩阵四合一
	}
	for(int i=1;i<=n;i++)base[i+n][i+n]=1;
	base=ksm(base,m-1);
	ans=ans*base;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			cout<<ans[i][j+n];
			if(j<n)cout<<' ';
		}
		cout<<'\n';
	}
	cout<<'\n';
	return 1;
}
int main(){
	for(int i=0;i<maxn;i++)I[i][i]=1;
	while(real_main());
}

[USACO07NOV]Cow Relays G

题意

给定一张 \(N\) 个点 \(M\) 条边的无向图，边有长度。

问从 \(S\) 到 \(T\) 经过 \(K\) 条边的最短路长度。

\(K\le10^6,M\le100,1\le u,v\le1000\)。

做法

首先，点的编号太大了，要离散化一下。于是 \(N\le 200\)。

看有很多倍增 \(\text{Floyd}\) 的做法。但这太麻烦了。我们来一个简单的做法。

还是先考虑 \(dp\)。

我们设 \(dp_{i,j}\) 从 \(s\) 开始经过 \(i\) 条边，到 \(j\) 的最短路。

那么转移就是：

\[dp_{i,j}=\min_{(k,i)\in E}dp_{i-1,k}+w(k,i) \]

这就很简单了。

于是，设 \(D_i=\begin{bmatrix} dp_{i,1} & dp_{i,2} & dp_{i,3} & \cdots & dp_{i,n}\end{bmatrix}\)。那么，转移矩阵就是：

\[base= \begin{bmatrix} w(1,1) & w(1,2) & w(1,3) & \cdots & w(1,n)\\ w(2,1) & w(2,2) & w(2,3) & \cdots & w(2,n)\\ w(3,1) & w(3,2) & w(3,3) & \cdots & w(3,n)\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ w(n,1) & w(n,2) & w(n,3) & \cdots & w(n,n) \end{bmatrix} \]

容易发现，矩阵乘法的加法应该改成取最小值，加法应该改成加法。

然后直接矩阵快速幂即可。

P6772 [NOI2020] 美食家

题意

给定一个 \(n\) 个点 \(m\) 条边的有向连通图，每个节点有一个价值 \(c_i\)，你从节点 \(1\) 出发。

边有边权 \(w\)，表示经过这条边要花费的天数。你不能在任何城市停留。

某些城市会在不同的时间举办美食节，一共会举办 \(k\) 次。如果你在这时刻到达了该城市，你会额外获得一定的价值。

问在第 \(T\) 天恰好到达节点 \(1\) 的前提下，求出走过的所有节点中价值之和最大是多少。

\(1 \leq n \leq 50\)，\(n \leq m \leq 501\)，\(0 \leq k \leq 200\)，\(1 \leq t_i \leq T \leq 10^9\)。

\(1 \leq w_i \leq 5\)，\(1 \leq c_i \leq 52501\)，\(1 \leq u_i, v_i, x_i \leq n\)，\(1 \leq y_i \leq 10^9\)。

做法

显然，设 \(dp_{i,j}\) 表示第 \(i\) 天在 \(j\) 号点的最大价值。

转移显然：

\[dp_{i,j}=\max_{(k,j)\in E}dp_{i-w(k,j),k} \]

因为 \(w_i\le 5\)，所以矩阵里面要记 \(5\) 天的dp值。那么矩阵边长就是 \(50\times 5=250\)。

转移矩阵显然。

那么单次矩阵乘法的复杂度就是 \(250^3=15625000\approx 1.5\times 10^7\)。考虑到还要分成 \(k\) 段处理，还有快速幂，显然这样复杂度是不行的。

考虑进行优化。

设 \(siz=n\times 5\)。不难发现，\(ans\) 矩阵是一个 \(1\times siz\) 的矩阵，\(base\) 矩阵是一个 \(siz\times siz\) 的矩阵，这两个矩阵做乘法的复杂度是 \(\Theta(siz^2)\) 的。

进行这次乘法会得到一个 \(siz\times siz\) 的新矩阵，但这个新矩阵只有第一行有效。所以又可以把这个新矩阵变成一个 \(1\times siz\) 的矩阵。

这样似乎就把矩阵快速幂优化到 \(siz^2\log_2T\) 了。但不难发现，矩阵快速幂是对 \(base\) 矩阵进行的，关你 \(ans\) 矩阵什么事。

所以考虑预处理出 \(base\) 矩阵的 \(2^k\) 次方次方。然后将指数二进制分解，让 \(ans\) 依次乘上即可。

这样，总复杂度就是 \(O(siz^2k\log_2T)\)，可以通过此题。

代码

写两种矩阵乘法。难调。

注意：美食节的时间不是按照升序给出的。

struct mat{//矩阵
	int val[maxn][maxn];
	mat(){//初始化为-inf
		memset(val,-0x3f,sizeof(val));
	}
};
struct fes{//美食节
	int t,x,y;
	bool operator < (const fes cmp){
		return t<cmp.t;
	}
}b[maxn];
int n,m,T,k;
int siz;
int a[maxn];
mat pw[maxn];
mat ans,base;
mat mul(mat a,mat b){//普通的矩阵乘法
	mat ans;
	for(int i=1;i<=siz;i++){
		for(int j=1;j<=siz;j++){
			for(int k=1;k<=siz;k++){
				ans.val[i][j]=max(ans.val[i][j],a.val[i][k]+b.val[k][j]);
			}
		}
	}
	return ans;
}
mat cheng(mat a,mat b){//平方复杂度的矩阵乘法
	mat ans;
	for(int i=1;i<=siz;i++){
		for(int j=1;j<=siz;j++){
			ans.val[1][i]=max(ans.val[1][i],a.val[1][j]+b.val[j][i]);
		}
	}
	return ans;
}
int getpos(int x,int y){
	return x+y*n;
}
int lowbit(int x){
	return x&(-x);
}
void ksm(int p){//改版快速幂
	for(;p;p-=lowbit(p))ans=cheng(ans,pw[__builtin_ctz(p)]);
}
signed main(){
	n=read(),m=read(),T=read(),k=read();
	siz=n*5;
	for(int i=1;i<=n;i++)a[i]=read();
	for(int i=1;i<=m;i++){//转移矩阵
		int u=read(),v=read(),w=read();
		base.val[getpos(u,w-1)][getpos(v,0)]=a[v];
	}
	for(int i=n+1;i<=siz;i++)base.val[i-n][i]=0;//转移矩阵
	for(int i=1;i<=k;i++)b[i].t=read(),b[i].x=read(),b[i].y=read();
	sort(b+1,b+1+k);
	pw[0]=base;
	for(int i=1;i<=n;i++)pw[i]=mul(pw[i-1],pw[i-1]);//处理base的2的k次幂次幂
	ans.val[1][1]=a[1];//初始化ans
	for(int i=1;i<=k;i++){
		ksm(b[i].t-b[i-1].t);
		ans.val[1][b[i].x]+=b[i].y;
	}
	ksm(T-b[k].t);
	if(ans.val[1][1]>=0)cout<<ans.val[1][1];
	else puts("-1");
	return 0;
}