sb(Stern-Brocot树 - 初绘

Ps：差连分数，连分数写法，模版题
Ps：啊啊啊啊，要疯了，快补完了，然后网页突然死掉了，再打开就没了（T-T...
Ps：感谢@Zelensky 告诉我有自动备份，真是太有用了，险
Ps：已补完
finish at 17:55 on 2025.7.4

作者在学习时搜集一些资料，并将他们整合，并添加了一些模版题，~~可能后续会添加一些有意思的题目~~

由于作者~~能力和笔法有限~~，可能有些地方衔接不连贯，见谅

提示：代码中 // 表示笔者写错过的地方

定义：

Stern–Brocot 树是一种维护分数的优雅的结构，包含所有不同的正有理数。

这个结构分别由 Moritz Stern 在 1858 年和 Achille Brocot 在 1861 年独立发现。

构造：

这棵树是由两个分数 $\frac{0}{1}$ 和 $\frac{1}{0}$ 起始的

分别表示两个边界 $0$ 和 $+\infty$ ,是第 $0$ 阶 $Stern–Brocot$ 序列

然后每次在相邻两个数 $\frac{a}{b}$ , $\frac{c}{d}$ 中间插入 $\frac{a + c}{b + d}$ 即可构成下一层序列

连成树时每一层删掉上一层已有的分数即可

下图非常直观，实线表示实际树边

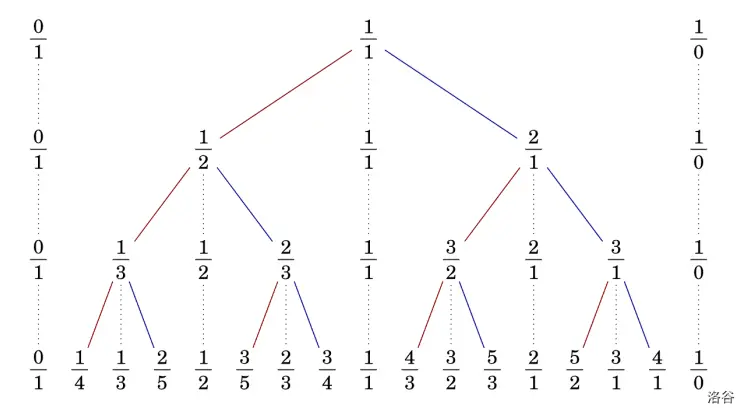
~~偷滴oi-wiki~~

矩阵和字符串表示

如果把构造过程用矩阵表示，每个数由 $\frac{a}{b}$ , $\frac{c}{d}$ 得来,表示为 $\begin{pmatrix} b & d\\ a & c \end{pmatrix}$
那根节点 $\frac{1}{1}$ 就是 $\begin{pmatrix} 1 & 0\\ 0 & 1 \end{pmatrix}$
向左走一步用矩阵 $\begin{pmatrix} 1 & 1\\ 0 & 1 \end{pmatrix}$ 表示
向右走一步用矩阵 $\begin{pmatrix} 1 & 0\\ 1 & 1 \end{pmatrix}$ 表示
读者可自己用矩阵乘法进行验证

同时由于每个分数在 $sb$ 树上的路径唯一，可以用唯一的 $LR$ 字符串表示

它称作 Stern–Brocot 数系。

性质

引理 1 ： $\frac{a}{b} < \frac{a + c}{b + d} < \frac{c}{d}$

证明恢常好证，直接交叉相乘即可

具体的
$\begin{aligned} \frac{a}{b} &< \frac{c}{d} \\ \\ a \times d &< b \times c \\ \\ a \times d + a \times b &< b \times c + a \times b \\ \\ a \times (b + d) &< b \times (a + c) \\ \\ \frac{a}{b} &< \frac{a + c}{c + d} \end{aligned}$

证毕，另一半同理

由此，其实我们也推出了单调性

引理 2：$sb$ 树中相邻的两个分数一定满足 $bc−ad=1$

考虑归纳证明，初始两个分数显然成立，考虑向中间插入 $\frac{a + c}{b + d}$ ，

相邻两个数为 $\frac{a}{b}$ 和 $\frac{a + c}{b + d}$ ，

$b \times (a + c) - a \times (b + d) = b \times c - a \times d = 1$

证毕

引理 3：任意一个值都是最简分数

同样归纳证明，由于 $b \times (a + c) - a \times (b + d) = 1$（引理 $2$），

$b \times (a + c) - a \times (b + d)$ 一定是 $gcd((a + c) , (b + d))$ 的倍数

所以 $(a + c) \perp (b + d)$

证毕

这也叫最简性

引理4 ：完全性：每一个既约分数（最简分数）都在 $sb$ 树中出现

证明这个oi-wiki的证明蒟蒻看懂啦

任意一个正分数都在 $0$ 到 $+\infty$ 之间，所以如果树中没有说明无限深

我们说明其不可能即可

假设现在已经知道
$\begin{aligned} \frac{a}{b} &< \frac{p}{q} < \frac{c}{d} \\ \\ \frac{a\times q}{b\times q} &< \frac{b\times p}{b\times q} \\ \\ \frac{a\times q}{b\times q} &\le \frac{b\times p - 1}{b\times q} \\ \\ b\times p - a\times q &\ge 1 , c\times q - p\times d \ge 1 \end{aligned}$

将两个不等式分别乘以 $(c+d)$ 和 $(a+b)$ ，就能够得到

$(c + d)\times (b\times p - a\times q) + (a + b)\times (c\times q - p\times d) \ge a+b+c+d$

化简得到
$p + q \ge a + b + c + d$

随着搜索不断加深，右式不断变大，而左式不变，搜索一定会终止

证毕

查找分数

1 朴素算法

很简单，直接在 $sb$ 树上暴力递归查找即可

代码：

void dfs(int a , int b , int c , int d) {
    if(a + c == p && b + d == q) {
        ...
        return ;
    }
    if(p * (b + d) < q * (a + c)) dfs(a , b , a + c , b + d);
    else dfs(a + c , b + d , c , d);
}

时间复杂度$O(p + q)$

摘：在 Stern–Brocot 数系中，每个正的无理数都对应着唯一的无限长的字符串。可以使用同样的算法构造出这个字符串。

这个无限长的字符串的每个前缀都对应着一个有理的最简分数。

将这些最简分数排成一列，数列中的分数的分母是严格递增的，而数列的极限就是该无理数。

因此，Stern-Brocot 树可以用于找到某个无理数的任意精度的有理逼近。

但是，应当注意的是，这个有理数数列和无理数之间的差距并非严格递减的。

在实际应用 Stern-Brocot 树寻找某个实数在分母不超过某范围的最佳逼近时，

最后应当注意比较左右区间端点到该实数的距离。

2 快速算法

注意到朴素算法太慢了，我们可以将连续的向左或向右移动合并来将其优化成 $O(log(p + q))$

原因每次左移加右移一定会使分子分母扩大至少两倍

设当前数表示 $\frac{a + c}{b + d}$ 为左移 $t_1$ 次，右移 $t_2$ 次，

连续 $t$ 次向右移动时，右侧边界保持不动，而左侧节点移动到 $\frac{a + t \times c}{b + t \times d}$ 处；

反过来，连续 $t$ 次向左移动时，左侧边界保持不动，而右侧节点移动到 $\frac{t \times a + c}{t \times b + d}$ 处

那么操作后的数为 $\frac{t_2 \times a + t_1 \times c}{t_2 \times b + t_1 \times d}$

显然成立

那具体怎么合并呢？

其实只要解 $\frac{a + t \times c}{b + t \times d} < \frac{p}{q},\frac{t \times a + c}{t \times b + d} > \frac{p}{q}$ 来确定向右和向左移动的次数

此处取严格不等号，是因为算法移动的是左右端点，而要寻找的分数是作为最后得到的端点的中位分数出现的。

代码：

void sol5(int a , int b , int c , int d , int p , int q) {
	while(1) {
		if(((a + c) == p) && ((b + d) == q)) {
			printf("%d %d %d %d\n",a,b,c,d);
			break;
		}
		int t = (b*p-a*q-1)/(c*q-d*p);
		if(t > 0) a = a + t * c, b = b + t * d;
			t = (c*q-p*d-1)/(p*b-a*q);
		if(t > 0) c = c + t * a; d = d + t * b;
	}
}

一般有分子分母约束的，写快速算法比较好一点

3.连分数实现

前置

这一部分需要一点连分数的前置知识

不多，如果只学 $sb$ 树学到递推关系就阔以啦

补充：递推关系证明（自己想的，不知道对不对，~~帮助更好背过~~）

考虑已经将 $[a_0 , ... , a_{n-1}]$ 表示为 $\frac{p}{q}$

其中 $p , q$ 为 $a_0 ... a_{n-1}$ 多项式

把 $a_{n - 1}$ 提出
$p = p' + k_1 \times a_{n - 1}$

$q = q' + k_2 \times a_{n - 1}$

在序列后添加一项 $a_n$ 后

根据定义，把 $a_{n - 1}$ 替换为 $a_{n - 1} + \frac{1}{a_n}$即可

即为 $\frac{p' + k_1 \times (a_{n - 1} + \frac{1}{a_n})}{q' + k_2 \times (a_{n - 1} + \frac{1}{a_n})}$

化简，上下同乘 $a_n$ ,得

$\frac{a_n \times (p' + k_1 \times a_{n - 1}) + k_1}{a_n \times (q' + k_2 \times a_{n - 1}) + k_2}$

$\frac{a_n \times p + k_1}{a_n \times q + k_2}$

其中 $k_1 , k_2$ 分别为 $[a_0 , ... a_{n - 1}]$ 时分子分母 $a_{n - 1}$ 的系数

由于 $[a_0 , ... a_{n - 1}]$ 时$a_n$ 的系数分别为 $p_{n - 1}$, $q_{n - 1}$ ,

所以 $k_1$ , $k_2$ 即为 $p_{n - 2} , q_{n - 2}$

所以替换可得
$\begin{aligned} p_n &= a_n \times p_{n - 1} + p_{n - 2}\\ q_n &= a_n \times q_{n - 1} + q_{n - 2} \end{aligned}$
得证

实现

考虑连分数与 $sb$ 树的关系

不妨假设首组移动是向右的；如果不然，则设首组向右移动的次数为零。

向右、向左交替移动端点 (记录拐点)，将每组移动后的端点位置排列如下：

$ \frac{p_0}{q_0} , \frac{p_1}{q_1} , ... , \frac{p_n}{q_n} $

奇数组移动是向右的，故而记录的是左端点的位置；（右端点不变）

偶数组移动是向左的，故而记录的是右端点的位置。（左端点不变）

在这一列端点前面再添加两个起始端点 $\frac{0}{1} , \frac{1}{0} $

设第 $k$ 组移动的次数为 $t_k$ , 根据树上搜索过程可得

$\frac{p_k}{q_k} = \frac{t_k \times p_{k-1} + p_{k - 2}}{t_k \times q_{k-1} + q_{k - 2}}$

~~有没有觉得这个东西很眼熟~~

没错这就是连分数的递推关系

将这个东西表示为 $[t_0 , ... , t_k]$

由于这是端点的递推

我们要的 $\frac{p}{q} = \frac{p_{n - 1} + p_n}{q_{n - 1} + q_n}$

即最后一次的系数为 $1$

所以 $\frac{p}{q}$ 表示为 $[t_0 , ... , t_n ， 1]$

我们求出 $\frac{p}{q}$ 的连分数表示，最后一个 1 去掉，即为 $sb$ 树上 $\frac{p}{q}$ 的搜索路径

注意第一步从右开始

因为如果系数为 $1$ , 就不用在意他是否和前一个合并

即 $[t_0 , ... , t_n ， 1] = [t_0 , ... , t_n + 1] $

这个可以根据递推关系自己模拟一下，很简单

代码放一下：

void zs(vector<int> v) {
	cnt = 2; P[1] = 0; P[2] = 1;
		 Q[1] = 1; Q[2] = 0;
	for(int i = 0;i < v.size();i ++) {
		cnt ++;
		P[cnt] = P[cnt - 1] * v[i] + P[cnt - 2];
		Q[cnt] = Q[cnt - 1] * v[i] + Q[cnt - 2];
	}
	printf("%d %d\n",P[cnt],Q[cnt]);
}

然后？

模版启动

P1797 【模板】Stern-Brocot 树

读者可以自己看一下题目，都是一些简单操作，挺好写的

第一个操作就是裸的求连分数，判断一下首尾即可
第二个操作用连分数的递推关系即可
第三个操作跑出两个分数的连分数，然后取公共部分，再用递推关系跑回分数即可
第四个操作就跑出连分数，然后取前 $k$ 个，再用递推关系跑回分数即可
1.第五个操作其实就是求这个分数是由哪两个分数插入的

可以先跑出他的连分数形式，减一即为父亲的连分数，根据定义求出另一个

2.第五个操作也可以用快速算法，好写一点

代码（比较长，求连分数其实可以提个函数：

点击查看代码

/*
write by C_Escape_Obsession
	  on 2025.7.2
数组要开到50
深度不用减一
辗转相除不用互质
*/
#include<bits/stdc++.h>
#define Pc pair<int,char>
#define Pi pair<int,int>
using namespace std;

const int N = 520;
int k;
int n[N];
char C[N];
void sol1(int p , int q) {
	vector<Pc> v;
	bool f = 1;
	while(q) {
		v.push_back({p / q , f ? 'R' : 'L'});
		p %= q; swap(p , q);
		f ^= 1;
	}
	v.back().first --;
	if(v[0].first) printf("%d %c %d ",v.size(),v[0].second,v[0].first);
	else printf("%d ",v.size() - 1);
	for(int i = 1;i < v.size();i ++) {
		if(v[i].first) printf("%c %d ",v[i].second,v[i].first);
	}
	printf("\n");
}
int P[N] , Q[N]; int cnt;
void zs(vector<int> v) {
	cnt = 2; P[1] = 0; P[2] = 1;
			 Q[1] = 1; Q[2] = 0;
	for(int i = 0;i < v.size();i ++) {
		cnt ++;
		P[cnt] = P[cnt - 1] * v[i] + P[cnt - 2];
		Q[cnt] = Q[cnt - 1] * v[i] + Q[cnt - 2];
	}
	printf("%d %d\n",P[cnt],Q[cnt]);
}
void sol3(int a , int b , int c , int d) {
	vector<Pc> v1; 
	bool f = 1;
	while(b) {
		v1.push_back({a / b , f ? 'R' : 'L'});
		a %= b; swap(a , b);
		f ^= 1;
	} 
	v1.back().first --;//
	vector<Pc> v2; 
	f = 1;
	while(d) {
		v2.push_back({c / d , f ? 'R' : 'L'});
		c %= d; swap(c , d);
		f ^= 1;
	} 
	v2.back().first --;//
	vector<int> v3;
	for(int i = 0;i < min(v1.size(),v2.size());i ++) {
		if(v1[i].second != v2[i].second) break;
		v3.push_back(min(v1[i].first , v2[i].first));
		if(v1[i].first != v2[i].first) break;
	}
	v3.push_back(1);//
	zs(v3);
}
void sol4(int dep , int a , int b) {
//	dep --;
	vector<Pc> v;
	bool f = 1;
	while(b) {
		v.push_back({a / b , f ? 'R' : 'L'});
		a %= b; swap(a , b);
		f ^= 1;
	}
	v.back().first --;
	vector<int> v2; int sum = 0;
	for(int i = 0;i < v.size();i ++) {
		if(sum + v[i].first >= dep) {
			v2.push_back(dep - sum);//
			sum = dep; break;//
		}
		sum += v[i].first;
		v2.push_back(v[i].first);
	}
	if(sum < dep) printf("-1\n");
	else v2.push_back(1),zs(v2);
}
void sol5(int a , int b , int c , int d , int p , int q) {
	vector<int> v;
	bool f = 1;
	a = p; b = q;
	while(b) {
		v.push_back(a / b);
		a %= b; swap(a , b);
		f ^= 1;
	}
	v.back() --;
	cnt = 2; P[1] = 0; P[2] = 1;
			 Q[1] = 1; Q[2] = 0;
	for(int i = 0;i < v.size();i ++) {
		cnt ++;
		P[cnt] = P[cnt - 1] * v[i] + P[cnt - 2];
		Q[cnt] = Q[cnt - 1] * v[i] + Q[cnt - 2];
	}
	c = p - P[cnt] , d = q - Q[cnt];
	if(1ll * c * Q[cnt] < 1ll * d * P[cnt]) swap(c , P[cnt]) , swap(d , Q[cnt]);
	printf("%d %d %d %d\n",P[cnt],Q[cnt],c,d);
}

int main() {
	int T; cin >> T;
	string s; int a , b , c , d , p , q;
	while(T --) { 
		cin >> s;
		if(s == "ENCODE_PATH") {
			scanf("%d%d",&p,&q);
			sol1(p , q);
		}
		else if(s == "DECODE_PATH") {
			scanf("%d",&k); vector<int> v;
			for(int i = 1;i <= k;i ++) 
				cin >> C[i] >> n[i];
			if(n[1] && (C[1] == 'L')) v.push_back(0);//
			for(int i = 1;i <= k;i ++) 
				v.push_back(n[i]);
			v.push_back(1);
			zs(v);
		}
		else if(s == "LCA"){
			scanf("%d%d%d%d",&a,&b,&c,&d);
			sol3(a , b , c , d);
		}
		else if(s == "ANCESTOR"){
			scanf("%d%d%d",&k,&a,&b);
			sol4(k , a , b);
		}
		else {
			scanf("%d%d",&p,&q);
			sol5(0 , 1 , 1 , 0 , p , q);
		}
	}
	return 0;
}

第五个操作另一种写法（快速算法）

void sol5(int a , int b , int c , int d , int p , int q) {
	while(1) {
		if(((a + c) == p) && ((b + d) == q)) {
			printf("%d %d %d %d\n",a,b,c,d);
			break;
		}
		int t = (b*p-a*q-1)/(c*q-d*p);
		if(t > 0) a = a + t * c, b = b + t * d;
			t = (c*q-p*d-1)/(p*b-a*q);
		if(t > 0) c = c + t * a; d = d + t * b;
	}
}

小结:如果没有分子分母的限制，连分数写法是最简单的，否则二者差不多

例题：

Ps：好难写啊，怎么没道正常题

1.P12469 [Math×Girl] 平均律

Ps：这道题作者学到了卡常技巧

题意：

我们定义一个数的近似分数为：

在允许的误差内分母最小的分数。

※ 这里允许分数的分母为 1。

请问允许的误差为 ±δ 时，

任选一数 ξ∈[0,1]，

其近似分数的分母为 n 的概率是多少？

$n∈[1,10^7],a,b∈[1,10^{18}]$

思路：

答案一定是很多段区间，我们考虑枚举每一个作为近似分数的数 $x = i / n$

找到它的前驱（定义为分母 $\le n$ 的第一个比 $x$ 小的分数） $l$

找到它的后继（定义为分母 $\le n$ 的第一个比 $x$ 大的分数） $r$

找到他们有什么用呢？

只要一个在 $l \sim r$ 的误差内不包含 $l$ 或 $r$ 的数的近似分数就是 $x$

用 $eps$ 表示误差,这个数的贡献就是：

$max(0, min(r−eps,x+eps) − max(l+eps,x−eps))$

解决

解决这个问题有线性做法

但好像没用 $sb$ 树，所以我们不讲，感兴趣的同学可以自行学习

观察前驱后继的定义，结合 $sb$ 树的性质（可以看图理解），

我们发现这就是 $sb$ 树 $x$ 到根路径上最后两个拐点

（原因很简单，路径上所有分数分母都小于 $x$ ，且每次移动边界一定离 $x$ 更近）

其实就是模版题第5个操作，求 $sb$ 树上 $x$ 为根的子树逼近值 / $x$ 是由那两个分数得来的

我用的是连分数递推求解

找到后用刚才那个柿子求解即可

不过有亿点卡常

卡常技巧（感谢blue_ice26大佬）

尽量少用 int128，不用double。

在枚举分数时去掉非最简分数不要去求最大公约数，分解质因数后再筛会更快。

少用除法，乘法会更快。

注意到 $n_i$ 与 $n_{n−i}$ 的贡献相同，可以直接省去一半的计算量。

作者踩的坑（T-T_）

分解质因数把 $n$ 变了

define int long long叉掉

是筛和 $n$ 有公共因数的，即非最简分数，笔者刚开始筛的因数...

过程中分数不用化简

$n == 1$ 需要特判，因为 0 / 1 不会枚举到且好像没有前驱后继

因为 $eps$ 是 $long long$ 范围的，做乘法要先给 $eps$ 取模

要比较大小的数先不取模

点击查看代码

#include<bits/stdc++.h>

#define ll long long
using namespace std;

const int N = 1e4 , mod = 998244353;
int n; 
ll a , b;
int p[N];
bitset<10000010> vis; 
inline void init() {
	for(int i = 1;i <= n;i ++) vis[i] = 0;
	int cnt = 0; int ddd = n;
	for(int i = 2;i <= sqrt((signed)n);i ++) {
		if(!(n % i)) {
			 p[++ cnt] = i;
			 while(!(n % i)) n = n/i;
		}
	}
	if(n != 1) p[++ cnt] = n;
	n = ddd;///
	for(int i = 1;i <= cnt;i ++) {
		for(int j = 1;j * p[i] <= n;j ++) {
			vis[j * p[i]] = 1;
		}
	}
}
inline int fastPow(ll x , int y) {
	ll s = 1;
	while(y) {
		if(y & 1) s = s * x % mod;
		x = x * x % mod; y >>= 1;
	}
	return s;
}
int P[N] , Q[N] , cnt;
struct node {
	ll x , y;
	node operator - (const node &c) const {
		node d;
		d.y = c.y * y;
		d.x = x * c.y - y * c.x;
		return d;
	}
	node operator + (const node &c) const {
		node d;
		d.y = c.y * y;
		d.x = y * c.x + x * c.y;
		return d;
	}
	bool operator < (const node &c) const {
		return (__int128)x * c.y < (__int128)y * c.x;
	}
}eps,eps2; ll ans;
inline void cz(int p , int q) {
	vector<int> v;
	int c1 = p , c2 = q;
	while(c2) {
		v.push_back(c1 / c2);
		c1 %= c2; swap(c1 , c2);
	}
	v.back() --;
	cnt = 2;
	for(int i = 0;i < v.size();i ++) {
		cnt ++;//
		P[cnt] = P[cnt - 1] * v[i] + P[cnt - 2];
		Q[cnt] = Q[cnt - 1] * v[i] + Q[cnt - 2];
	}
	int c = p - P[cnt] , d = q - Q[cnt];
	if(c * Q[cnt] < d * P[cnt]) swap(c , P[cnt]) , swap(d , Q[cnt]);
	node l = (node){P[cnt] , Q[cnt]} , r = (node){c , d} , s = (node){p,q};
	if(r - l < eps2) return ;
	int a1 , a2;
	//eps 先mod
	if(r - s < eps2) 
		a1 = ((eps.y%mod*r.x%mod-eps.x%mod*r.y%mod+mod)%mod)*fastPow(eps.y%mod*r.y%mod,mod-2)%mod;
	else a1 = ((eps.y%mod*s.x%mod+eps.x%mod*s.y%mod+mod)%mod)*fastPow(eps.y%mod*s.y%mod,mod-2)%mod;
	if(eps2 < s - l)
		a2 = ((eps.y%mod*s.x%mod-eps.x%mod*s.y%mod+mod)%mod)*fastPow(eps.y%mod*s.y%mod,mod-2)%mod;
	else a2 = ((eps.y%mod*l.x%mod+eps.x%mod*l.y%mod+mod)%mod)*fastPow(eps.y%mod*l.y%mod,mod-2)%mod;
	ans = ((ans + a1 - a2) % mod + mod) % mod;
}
inline void solve() {
	for(int i = 1;i <= n/2;i ++)
		if(!vis[i]) cz(i , n);
}
/*1
961 868471679412 342706800613471648*/

signed main() {
	long long T; cin >> T;
	P[1] = 0; P[2] = 1;
	Q[1] = 1; Q[2] = 0;
	while(T --) {
		ans = 0;
		scanf("%d%lld%lld",&n,&a,&b);
		eps = (node){a , b}; eps2 = node{a*2ll,b};
		if(n == 1) {
			if(a * 2 >= b) {printf("1\n");continue;}
			else {
				printf("%lld\n",a * 2ll % mod * fastPow(b%mod , mod - 2) % mod);
				continue;
			}
		}
		init(); solve();
		if(n != 2) ans = (ans << 1) % mod;//
		printf("%lld\n",ans);
	}
	return 0;
}

2.P1298 最接近的分数

题意：

给出一个正小数，找出分子（分子 ≥0）不超过 M，分母不超过 N 的最简分数或整数,

使其最接近给出的小数。“最接近”是指在数轴上该分数距离给出的小数最近，

如果这个分数不唯一，输出 "TOO MANY"

$1≤M,N≤10^7$

解法：

显然是一道有理逼近的板子

发现数据范围很小

~~直接在 $sb$ 树上暴力~~

能暴力为什么消费自己呢

点击查看代码

#include<bits/stdc++.h>
#define int long long
using namespace std;

long long n , m;
double abc(double x) {
    return x > 0 ? x : -x;
}
pair<int,int> ans = {0 , 1}; double Mi , s;
bool flag;
void dfs(int a , int b , int c , int d) {
	double k = (a + c) * 1.0 / (b + d);
	if(a + c > m || b + d > n) return ;
	if(abc(Mi - s) == abc(k - s)) flag = 1;
	if(abc(Mi - s) > abc(k - s)) ans = {a + c , b + d} , Mi = k , flag = 0;
	if(k > s) dfs(a , b , a + c , b + d);
	else dfs(a + c , b + d , c , d);
}

signed main() {
	cin >> m >> n;
	cin >> s;
	dfs(0 , 1 , 1 , 0);
	if(flag) printf("TOO MANY");
	else printf("%lld/%lld",ans.first , ans.second);
	return 0;
}

3.AT_abc333_g [ABC333G] Nearest Fraction

Ps：笔者学会了重载

题意：

给定一个小于 $1$ 的正实数 $r$ 和一个正整数 $n$。

要求在满足 $0≤p≤q≤n$ 和 $gcd(p,q) = 1$ 的前提下，找到使 $∣r−\frac{p}{q}∣$ 最小的二元组 $(p,q)$ 。

如果存在多个这样的二元组 $(p,q)$，输出 $p/q$ 值最小的那个。

数据范围：$1≤n≤10^{10}，r∈(0,1)$ 且最多包含 $18$ 位有效数字。

解决：

这题是正经的有理逼近，不能暴力

那就用快速算法

你以为就结束了？

注意到这题精度很高，正常会炸

一步比较巧妙是把 $r$ 直接换成分数，就是有点大，要开 $int128$

然后这题有很多边界需要注意，第一次写还是挺难受的

点击查看代码

#include<bits/stdc++.h>
#define int __int128
using namespace std;

long long n;
int x , y;
int abc(int x) {
    return x > 0 ? x : -x;
}
struct node {
	int a , b;
	void cr() {
		if(a) { int c = __gcd(a , b); a /= c, b /= c; }
		else b = 1;
	}
	node operator - (const node & c) const {
		node d; d.b = b * c.b;
		d.a = abc(a * c.b - b * c.a);
		d.cr(); return d;
	}
	bool operator >= (const node & c) const {
		return a * c.b >= b * c.a;
	}
}r , ans;
void print(__int128 x) {
  if (x < 0) { putchar(  '-'); x = -x; }
  if (x > 9) print(x / 10);
  putchar(x % 10 + '0');
}
void dfs(int a , int b , int c , int d) {
    if((node){1 , 1} - r >= ans - r) {} else ans = (node){1 , 1};//
	bool f = 1;
	while(a + c <= n && b + d <= n) {
        if(ans - r >= (node){a + c , b + d} - r) ans = (node){a + c , b + d};
		if(f) {
			int t = min({(n - a) / c , (n - b) / d , (b * r.a - a * r.b) / (r.b * c - r.a * d)});
			if(t > 0) a += t * c , b += t * d;
			if(ans - r >= (node){a , b} - r) ans = (node){a , b};
		}
		else {
			int t = min({(n - d) / b , (c * r.b - d * r.a) / (b * r.a - a * r.b)});
	
			if(a) t = min((n - c) / a , t); 
			if(t > 0) c += t * a , d += t * b;
			if((node){c , d} - r >= ans - r) {}else ans = (node){c , d};
		}
		f ^= 1;
	}
}
string s;

signed main() {
	cin >> s; r.b = ans.b = 1;
	for(int i = 2;i < s.size();i ++) r.a = r.a * 10 + s[i] - '0' , r.b = r.b * 10;
	r.cr();
	cin >> n;
    if(r.a <= n && r.b <= n) {ans = r; }//
	else dfs(0 , 1 , 1 , 1);
	printf("%lld %lld",(long long)ans.a , (long long)ans.b);
	return 0;
}

posted on 2025-07-03 17:30 初绘阅读(110) 评论(1) 收藏举报

刷新页面返回顶部

定义：

构造：

矩阵和字符串表示

性质

引理 1 ： \(\frac{a}{b} < \frac{a + c}{b + d} < \frac{c}{d}\)

引理 2：\(sb\) 树中相邻的两个分数一定满足 \(bc−ad=1\)

引理 3：任意一个值都是最简分数

引理4 ：完全性：每一个既约分数（最简分数）都在 \(sb\) 树中出现

查找分数

1 朴素算法

2 快速算法

3.连分数实现

前置

实现

模版启动

例题：

1.P12469 [Math×Girl] 平均律

题意：

思路：

解决

2.P1298 最接近的分数

题意：

解法：

3.AT_abc333_g [ABC333G] Nearest Fraction

题意：

解决：