1060 爱丁顿数 (25 point(s))
// 18 points
#include <bits/stdc++.h>
using namespace std;
int main() {
int n, days = 0;
// key存储距离 val存储距离累积的天数
map<int , int> E;
cin >> n;
while(n--){
int tmp;
cin >> tmp;
E[tmp]++;
}
// 缓存首地址的距离
auto a = E.begin();
// 判断当前距离是否小于或等于当前累积的天数
for(auto b = E.rbegin(); ; b++){
// 向下累积天数
days += b->second;
// 如果当前累积的天数 超过 当前公里则为 爱丁顿数
if(b->first < days){
cout << b->first;
break;
}
// 如果 b 指向了首个元素但还没有获得爱丁顿数
// 说明距离仍然大于天数 但因为没有更小的距离了
// 故直接输出当前累积的天数
if(b->first == a->first){
cout << days;
break;
}
// 否则指向并处理下一个数
}
}
// 21 points
#include <bits/stdc++.h>
using namespace std;
int main() {
int n, days = 0;
// key存储距离 val存储距离累积的天数
map<int , int> E;
cin >> n;
if(n == 0) { cout << 0; return 0;}
for(int i = 0; i < n; i++){
int tmp;
cin >> tmp;
E[tmp]++;
}
// 获取容器首地址比较最低距离和骑行天数
// 最低距离大于骑行天数 输出骑行天数
if(begin(E)->first > n) cout << n;
// 最低距离等于骑行天数 输出骑行天数 - 1
else if(begin(E)->first == n) cout << n - 1;
else{
for(auto b = E.rbegin(); ; b++){
// 向下累积天数
days += b->second;
// 如果当前累积的天数 超过 当前公里则为 爱丁顿数
if(b->first < days){
cout << b->first;
break;
}
}
}
}
// 25 points
#include <bits/stdc++.h>
using namespace std;
int main() {
int n, days = 0;
// key存储距离 val存储距离累积的天数
map<int , int> E;
cin >> n;
for(int i = 0; i < n; i++){
int tmp;
cin >> tmp;
E[tmp]++;
}
// 获取容器首地址比较最低距离和骑行天数
// 最低距离大于骑行天数 输出骑行天数
if(begin(E)->first > n) cout << n;
// 最低距离等于骑行天数 输出骑行天数 - 1
else if(begin(E)->first == n) cout << n - 1;
else{
// 从最大距离开始向小遍历 直到 i 距离 <= 累积天数
int i;
for(i = (E.rbegin())->first; i >= 0 && i > days; i--){
// 向下累积天数
days += E[i];
}
// 如果当前累积的天数 超过 当前公里则为 爱丁顿数
cout << i;
}
}
// 25 points 另一种思路
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n;
cin >> n;
vector<int>kile(n);
for (int i = 0; i < n; i++)
cin >> kile[i];
sort(begin(kilo), end(kilo));
// 0-n升序距离数组 n-0降序天数下标
for (int i = 0; i < n; i++)
if (kilo[i] > n - i)
{
cout << n - i;
return 0;
}
// 如果没有找到说明是 0 的特例
cout << 0;
}
原来如此,我们最开始看到条件 E 天数超过距离 E 时候,还以为这两个是同一个变量了。故也就以为这两个应该是相等的。
但里面有一个 “超过” 要判断骑行距离要大于天数。
最开始只过了样例,然后调了调试然后发现 rbegin() 会遍历到出界,所以加了一个首元素的判断。
然后想如果有几天距离很大,但是后面的跟不上,比如说 N = 4 但是有四天都是 10 10 10 10 的情况。这时候就需要输出天数作为爱丁顿数。这样只是过了测试点三。
然后又看了看别人的描述,发现题目的是“超过”,没错又是超过然后我又写成了等号 b->first <= days 当距离小于等于累积的天数时输出。所以得谨记™的超过是没有等于的 = 。
但就这样也就多过了最后一个测试点得了18分。
所以后面又去找别人的测试例子,发现有一个盲点没有考虑 n = 3 数据是 3 4 4 的时候,结果应该是 2 。这让我想了想当时的思路。因为当时以为可以从高位开始累积,然后向下不断累积天数,使得最后可以令累积的天数大于距离。但这个例子说明,这个想法并不成立。
比如这个例子 E = 3,4 都是不成立的。根据条件 “E 天骑车超过 E 英里”,遍历到 4 累积天数是 2 但需要超过 4 所以需要天数至少是 5,遍历到 3 累积天数是 3 但需要天数 4 ,只有到 2 的时候 累积天数是 3 需要天数是 3 这时才能够满足条件输出 2 。
所以从一开始忽略 “超过” 字眼的时候,分析的条件就错误了。
所以在新的思路上,重新考虑应该怎么判断。题目样例所给出数据是骑行天数大于给出距离数据的最小值。
10 6 时 前面超过距离 6 累积天数 6 故满足条件
10 9 8 8 7 7 6 6 3 2
1 2 3 4 5 6 7 8 9 10
在这种情况下,我们可以在所给出的距离中找到令 E 天 超过距离 E 的情况
4 累积天数 4
10 10 10 10
1 2 3 4
3 累积天数 3
5 5 4
1 2 3
上面的两个例子,给出的数据累积天数分别是 4 和 3,而最低距离分别为 10 和 4 。而若以题目给出的距离是远不能满足累积天数的条件的。更多距离需要满足更多的天数,显然我们目前是少于的情况,因此只能向距离减少的方向处理。
如果我们用容器 map ,显然无法遍历比给出距离数据小的情况。用 map 读取倒是挺顺利,但是处理时候就不行了。
(其实也不是不行,直接用下标 i 加 map 也是可以对,因为用 map 读取空的 key 的时候 val 自然会重置为 0 这不会影响我们处理时候的情况)
再思考一个情况,什么时候刚好输出骑车的天数 N?
首先输出 N 必然不可能是上面第一类情况,因为距离数据中间能够找到结果,直接就输出了。所以输出全部累积天数必然是第二类情况,上面的例子都可以直接输出骑车的天数 N。
还有一种情况,下面再给一个例子。
3 累积天数 3
4 4 3
1 2 3
累积天数是 3 ,但是我们能够直接输出累积天数或者骑车天数 N = 3 吗,显然不行,因为现在最低距离是 3 不满足天数超过距离的条件。所以我们只能够将天数递减,直到天数能够满足给出数据的最低距离。此处答案为 2 , 2 的时候需要满足 2 天 并且大于 2 的骑行距离也就说这里最低的距离 3 。
但是 2 在给出的距离数据之外,所以需要手动减去累积的天数以最终小于给出的最低距离。
所以我们可以看到三种情况:
-
最低距离小于骑行天数 N 结果在给出的数据中找到
-
最低距离等于骑行天数 N 结果为骑行天数 N - 1
-
最低距离大于骑行天数 结果直接输出骑行天数 N
分析半天只是多过了测试点二得21分,继续看别人代码。
又看到别人一种测试数据,当最低距离小于骑行天数,但是爱丁顿数却在最低距离前面。
5 累积天数 5
10 10 10 10 3
1 2 3 4 5
比如这个例子,结果应该是 4 。虽然最低距离是 3 但是前面四个 10 已经能够满足爱丁顿数的条件即 4 ,并且这个还比 3 大,故结果就是 4 而不是从 3 继续往小了算并打算包括 3 。
而出现这个问题的原因在于 map 容器只能够遍历前面填入过的元素。这里只出现了 10 和 3 但是并没有对 10 和 3 中的元素进行判断。(前面提过)
而上面的分类只解决了骑行天数小于或者等于最低距离的情况,而并没有解决结果可能在最低距离和最高距离的数据,但是没有下标能够遍历的情况。
所以用上面考虑过的解决办法,来解决下这个问题。先获取最大距离,作为循环条件,然后向小的情况进行遍历,以找到可能的下标。
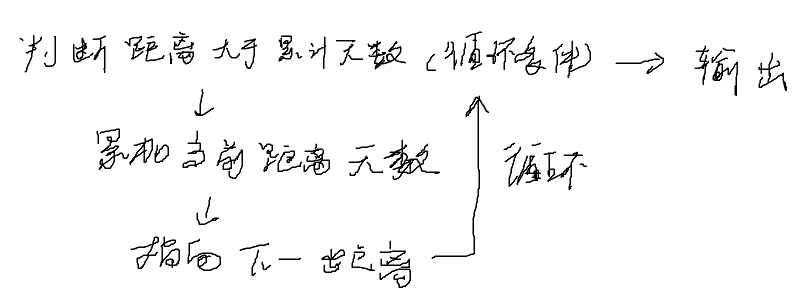
当指向下一距离,即下标的时候会进行判断,如果前面的距离累积的天数已经满足等于当前距离的时候,也就满足题目条件 “天数E超过距离E” 了。
比如样例的 10 9 8 8 7 7 6 指向 6 的时候前面有超过 6 的 6天。所以 6 是爱丁顿数。或者前面的 10 10 10 10 3 指向 4 的时候前面有超过 4 的 距离 10 的四天,这使得 4 是结果。
满足这个样例后通过全部测试点。
当时执着到处找参考文章的原因是想找到跟当时思考类似的切入点,并尝试找到里面的盲点以解决,而不是直接将别人的思路架空在自己的思路之上,更何况别人的思路不一定是自己能够理解的。
对于这种题目比较缺乏思路,不是很能理解为什么别人能够想到这样的建模的方式,又因为什么特征从而想到这样的方法。缺乏这样条件时候在解题只能根据样例或者某些测试数据一个个摸索思考了。
而参考有些文章,虽然能够很快记住别人使用的方法,但是如果不理解用这个方法的原因或者动机,很多时候是无法将学到的方法应用在其他题目中。而很多参考的文章就缺少这种方法背后使用的动机或者原因的描述,上来就给一个方法了或者仅仅只是描述了一下方法,但对于给出方法的思考回路没有一点提及,让人读得辛苦。
到底是因为这种题目以前见过,能够看出里面的某些特征跟本题相似,所以尝试使用了这样的方法,还是因为这类题目其实是某类模板,这种题型可以对应这样的思考的方法。或者是这种方法可以匹配这样的题目条件等等。
不过实际解题中肯定不可能还能像平时写的时候一样有这么多测试样例给自己去理解不同的处理情况,去编写代码。要么自己有处理过类似的边界情况,从而有这样的意识,或者就是从题目的数据和条件中抽象模型,来建立一个处理的方法,就不必想这样穷举情况来编写代码。
参考了别人的文字,发现之前所考虑的方向大多是从题目给出的骑行天数,累积到中间的时候的累积天数或者距离,并尝试找到这些变量中与满足题目条件的关系。
并没有以连续的天数作为对象考虑,建立下标,找到对应距离是否满足条件关系。而改变思考对象后,一切都会变得更加简单,不必像前面几个对象一样考虑这么多情况。一条龙就可以满足多个问题了。
E 天骑车超过 E 英里的最大整数 E
而且题目描述也是以天数最先描述到的,所以是否可以考虑先定天作为一个变量,再考虑距离(以题目给出的变量的先后顺序,建立变量间的关系)。
思路是将距离升序,天数降序。
开始E天超过E英里
骑行距离:2 3 6 6 7 7 8 8 9 10
骑行天数:10 9 8 7 6 5 4 3 2 1
可以看到,第6天的时候开始距离都能够超过天数,满足题目条件,前面都因为距离小于天数不满足“超过”条件。而因为随着距离继续增大,天数开始减少,所以第一个满足的就是最大的爱丁顿数。
所以我们可以距离超过天数作为爱丁顿数的判断(前面是累积的天数超过距离)。
E
骑行距离:10 10 10 10
骑行天数:4 3 2 1
E
骑行距离:4 5 5
骑行天数:3 2 1
E
骑行距离:3 4 4
骑行天数:3 2 1
E
骑行距离:3 10 10 10 10
骑行天数:5 4 3 2 1
可以看到用这样的方式,这些样例都能够得到结果。
但有一种情况需要特殊处理。
骑行距离:1
骑行天数:1
当只输入 1 距离的时候,因为无法继续向后遍历,并且没有比 1 更小的天数,所以无法通过这个方式得到 0 的结果。这种情况需要特殊处理,否则测试点四会错。
所以后面对这种题目,可以思考是否应该对这些数据进行排序,改变之间的对应关系,或者参考其他题目的,是否可以分类,或者标记特殊变量和数据。并将处理后的数据展现出来,看看是否能够找到什么规律或者能否满足什么条件。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号