1007 素数对猜想 (20 point(s))

#include <bits/stdc++.h> 
using namespace std;

bool prime(int p){
	// 如果是平方要取等号 
	for(int i = 2; i <= sqrt(p); i++){
		if(p % i == 0) return false;
	}
	return true;
}

int main(){
	int cnt = 0, n;
	vector<int> v;
	cin >> n;
	
	// 获取 2 - n 素数
	for(int i = 2, cnt = 0; i <= n; i++){
		if(prime(i) == true)
			v.push_back(i);
	} 
	
	for(int i = 0; i < v.size() - 1; i++){
		if(v[i+1] - v[i] == 2) cnt++;
	} 
	cout << cnt;
}

v[i] < n

当时素数对的判断写了这个东西。但是写的时候就觉得有问题的，因为当前是 v[n] 但是需要判断下一个 v[n+1] 下一个素数，可能当前 v[n] < n 但是 v[n+1] 却超出前面获取的素数表的范围，越界了。

当然结果也很必然的 Segmentation Fault 指针错误了。

---

当时还在疑惑，为什么用向量的话，写成 i < v.size() 没事，因为 i 从 0 开始， i + 1 就会遍历到 size() 显然就越界了。但是无论写成 size() - 1 还是 size() 居然都可以全部 AC 。打印一看才知道是怎么回事。

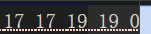
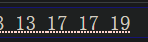
上面是 size() 下面是 -1 ，可以看到越界后的向量的元素居然自动变成了 0 当然 0 不可能满足题目的素数对的条件，也就不会使得判断错误而结果有问题了。但是这样写 i + 1 必然是越界了，0 就不是原来素数表里面有的元素。所以 size( ) - 1 才是严谨的。

参考代码

---

v[i+1] < n

顺手打印下刚才写的错误的判断，即便是 v[i+1] 也是错的，因为素数表最大就获取到 n 怎么可能会有大于 n 的素数， 所以必然是存在错误的。还是直接用下标遍历，明确有多少个变量。

---

获取素数的范围有两种，要么是 i < p 要么是现在代码里面写的 i <= sqrt(p) ，当时错误将后者写成 i < sqrt(p) 结果少了一些素数。

因为后者在算法导论里面提到过， 将 k 作为约数的话，因数也可以，那么 k * (n / k) = n = (√n)^2 所以 k 作为 n 的约数，必然要小于并等于 √n 才能和 n / k 相乘等于 n。而且上面也写了一个 = 等号了。

而 i < p 的缘故是不需要判断 p 本身，找比 p 小的因数，思路不太一样。

而且也因为 i < p 的习惯，连题目的要求也写错了，题目说的是不超过 n 的素数对的判断。结果也写了一个 i < n， 少了对 n 的判断，又错了几个测试点（似乎栽在“不超过”，这个关键词上好几次了）。

不超过N