1050 螺旋矩阵 (25 point(s))(未AC错误代码,仅错误思路记录)
#include <bits/stdc++.h>
using namespace std;
int main() {
int N, m, n;
set<int> num;
cin >> N;
// 待填充序列
for(int i = 0; i < N; i++){
int tmp; cin >> tmp;
num.insert(tmp);
}
for(auto n: num) cout << " " << n;
cout << endl;
// 找出 m 和 n
// 满足 m * n = N m ≥ n
// m - n 尽可能小意味着 m 无限接近 n
for(n = 1, m = N; n <= N; n++){
int tmp = N / n;
if(n > tmp) break;
m = tmp;
// cout << m << " " << n << endl;
}
cout << m - 1 << " " << n - 2 << endl;
n--;
// N个 非递增 左上角开始 顺时针填入
// row col 行列 以及当前矩阵的边界位置
int row = 0, col = 0, up = 0, right = n - 1, down = m - 1, left = 0, a[m][n];
for(auto n : num){
// 顺时针判断 判断是否到边界到边界 变向并更新边界
cout << row << " " << col << " ";
// 上边界向左移动++
if(row == up){
// 到达右边界向下移动 上边界向下递减
if(col == right){
up--;
continue;
}
a[row][col] = n;
++col;
}
// 右边界向下移动++
else if(col == right){
// 到达下边界向左移动 右边界向左递减
if(row == down){
right--;
continue;
}
a[row][col] = n;
++row;
}
// 下边界向左移动--
else if(row == down){
// 到达右边界向上移动 下边界向上递增
if(col == left){
down++;
continue;
}
a[row][col] = n;
--col;
}
// 左边界向上移动--
else if(col == left){
// 到达上边界像右移动 左边界向右递增
if(row == up){
left++;
continue;
}
a[row][col] = n;
--row;
}
}
cout << endl << m << " " << n << endl;
for(int i = 0; i < m; i++){
int flag = 0;
for(int j = 0; j < n; j++)
cout << (flag++ ? " " : "") << a[i][j];
cout << endl;
}
}
#include <bits/stdc++.h>
using namespace std;
int main() {
int N, m, n;
set<int> num;
cin >> N;
// 待填充序列
for(int i = 0; i < N; i++){
int tmp; cin >> tmp;
num.insert(tmp);
}
for(auto n: num) cout << " " << n;
cout << endl;
// 找出 m 和 n
// 满足 m * n = N m ≥ n
// m - n 尽可能小意味着 m 无限接近 n
for(n = 1, m = N; n <= N; n++){
int tmp = N / n;
if(n > tmp) break;
m = tmp;
// cout << m << " " << n << endl;
}
cout << m - 1 << " " << n - 2 << endl;
n--;
// N个 非递增 左上角开始 顺时针填入
// row col 行列 以及当前矩阵的边界位置
int row = 0, col = 0, up = 0, right = n - 1, down = m - 1, left = 0, a[m][n];
cout << right << " " << down << endl;
for(auto n : num){
// 顺时针判断 判断是否到边界到边界 变向并更新边界
a[row][col] = n;
cout << row << " " << col << " ";
// 上边界向左移动++
if(row == up){
// 到达右边界向下移动 上边界向下递减
if(col++ == right){
up--;
col--;
// 要像下运动
row++;
}
}
// 右边界向下移动++
else if(col == right){
// 到达下边界向左移动 右边界向左递减
if(row++ == down){
right--;
row--;
col--;
cout << "你在搞什么?";
}
}
// 下边界向左移动--
else if(row == down){
// 到达右边界向上移动 下边界向上递增
if(col-- == left){
down++;
col++;
row--;
}
}
// 左边界向上移动--
else if(col == left){
// 到达上边界像右移动 左边界向右递增
if(row-- == up){
left++;
row++;
col++;
}
}
}
cout << endl << m << " " << n << endl;
for(int i = 0; i < m; i++){
int flag = 0;
for(int j = 0; j < n; j++)
cout << (flag++ ? " " : "") << a[i][j];
cout << endl;
}
}
调试后发现这个up都写错了,应该是++而不是--。
但是果然会出现这个问题,如果到达边界时候移动边界,下一个位置与边界重合,导致继续认为在上一边界上,从而无限循环。
不过我们还是不继续调试了,从一开始决定思路的时候就有问题。对于这种题目,从一开始定下大思路就有问题的时候,后面实现都是在无尽的钻牛角尖。看柳诺的代码还是画了图并且尝试给出具体的实现方案的。我们什么没有在草稿上面实现,仅仅只是有一个模糊的思路就直接写了下去,没有考虑具体的细节,自然会导致现在无限的debug。
记忆下错误尝试中发现的写的时候的问题,发现打断点调试还是比其全部打印,用 cout 输出信息要直观不少,可以了解到动态的过程中数据的变化。
所以有以后可以多调试,掌握点调试技巧,有助于debug。
一开始令 n = 0 开始,但是因为 n 会作为分母,如果为 0 会运算问题。所以以后有除法运算的时候注意分母的边界。
错误的思路当时以为每一个边界固定的,然后判断当前是哪一个边界上然后给出元素。但是错了这么多才想到,以当时的思路是会导致 边界重合的,并且还有上面的,由于移动边界导致下一个元素的位置又在边界上,从而无限循环。
| 上1 | 上1 | 上1 | 上1/右1 |
|---|---|---|---|
| 左1 | 右1 | ||
| 左1 | 右1 | ||
| 下1/左1 | 下1 | 下1 | 右1/下1 |
比如看这个表格,右上右下左下的边界如果按照这样的方式,都重合在了一起,那么判断的时候怎么解决?这是一个问题。
还有就是如果按照当时的思路,到达上1边界并且到达右1边界的时候,会令上边界下移,那么下移后下一个要输出的元素位置恰好又在上边界上,这必然会导致下一步错误。
| 上1 | 上1 | 上1 |
|---|---|---|
| 左1 | 上1/右1 |
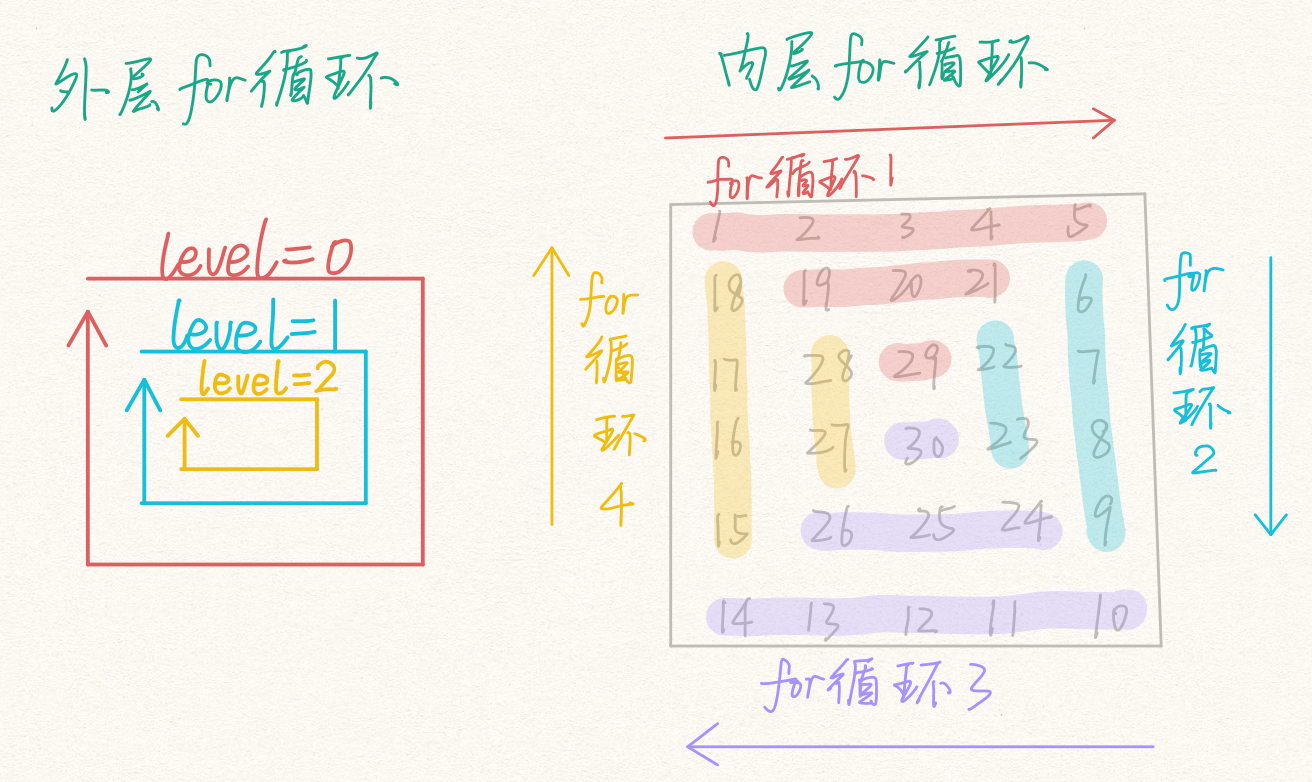
借用柳诺大神的图片,可以看到,别人在考虑的时候是把边界的重合通过行比列多占据位置来解决的。同时一个很重要的点是别人是通过给定的循环变量来输出元素的,而不是按照本人此处的思路,通过判断的方式来决定在哪一个边界上。
其实当时有这样的思路的原因是因为不晓得怎样计算最内层结束循环的边界,故采用了遍历原始序列所有元素的方式,然后判断在哪一个边界上来决定输出位置。
但这样思考的方向就会导致上面的诸多问题,比如边界判定问题,位置和边界移动问题,还有判断时候 ++col == right 边界判断的自增自减到底是放在变量前面还是后面,又到底是在判读前输出位置元素,还是判断后等等。
还有就是,看了别人的思路后,感觉这个应该思考的方向类似于图案输出,什么正方形菱形三角形等等。而这里是一个回文一样的长方形。
除了输出出来的考虑外,当时在判断边长得到 m n 上也没有很好理解。因为题目给出了条件“m−n 取所有可能值中的最小值”,而参考别人的方法是令 n 从大向小开始遍历的,而本人原先的思路是从小向下遍历的,这就可能会不满足这个条件。
突然想起来,之前写某题的时候总结,应该将不同的子步骤拆分,然后分步实现。这次又犯了所有一起实现的毛病。
虽然思路错了,但在不知道错误的时候,实现的思路应该是先将上边界正确打印出来,然后尝试写拐角并挪到右边界,然后接着下边界左边界。这样分步的思路去逐一实现。
否则就像这次又把所有一起实现,显然就导致各个步骤之间的bug聚集在一起,然后解决起来就会花费更多的精力理解这些bug到底对应哪一个步骤上面。
[========]
#include <bits/stdc++.h>
using namespace std;
int main() {
int N, m, n;
vector<int> num;
cin >> N;
// 待填充序列
for(int i = 0; i < N; i++){
int tmp; cin >> tmp;
num.push_back(tmp);
}
sort(begin(num), end(num), greater<int>());
for(auto n: num) cout << " " << n;
cout << endl;
// 找出 m 和 n
// 满足 m * n = N m ≥ n
// m - n 尽可能小意味着 m 无限接近 n
for(n = 1, m = N; n <= N; n++){
int tmp = N / n;
if(n > tmp) break;
m = tmp;
// cout << m << " " << n << endl;
}
// cout << m - 1 << " " << n - 2 << endl;
n--;
// N个 非递增 左上角开始 顺时针填入
// row col 行列 以及当前矩阵的边界位置
int row = 0, col = 0, up = 0, right = n - 1, down = m - 1, left = 0, a[m][n];
int first = 0;
fill(a[0], a[0] + m * n, 0);
cout << right << " " << down << endl;
for(auto n = begin(num); n != end(num); ++n){
// 输出左上角
if(first++ == 0) {
a[row][col] = *n;
continue;
}
// 每移动一次都要输出
// 判断上边界
if(row == up){
// 上边界向右++移动
++col;
a[row][col] = *n;
// 判断下一个是右边界则向下++ 并改变边界
if(col == right){
++row, ++up;
a[row][col] = *(++n);
}
}
else if(col == right){
// 右边界向下++移动
++row;
a[row][col] = *n;
// 判断下一个是下边界则向左-- 并改变边界
if(row == down){
--col, --right;
a[row][col] = *(++n);
}
}
else if(row == down){
// 下边界向左--移动
--col;
a[row][col] = *n;
// 判断下一个是左边界则向上-- 并改变边界
if(col == left){
--row, --down;
a[row][col] = *(++n);
}
}
else if(col == left){
// 左边界向上--移动
--row;
a[row][col] = *n;
// 判断下一个是上边界则向右++ 并改变边界
if(col == left){
++col, ++left;
a[row][col] = *(++n);
}
}
}
cout << m << " " << n << endl;
for(int i = 0; i < m; i++){
int flag = 0;
for(int j = 0; j < n; j++)
cout << (flag++ ? " " : "") << a[i][j];
cout << endl;
}
}
原来给出的待填充的数是有重复的,题目没有提都没注意,没有怎么考虑就用了 set 容器来方便排序了。结果重复的元素被吃掉了。
还有就是发现 vector 原来不能排序的时候像数字那样 sort(vector, vector + n),得用 begin() 和 end() 才行。 + n 改变地址是数组的专属。
虽然有点傻逼不想再往这个思路思考了, 但还是忍不住想用一下刚才学到的拆解和调试的方式看看这个思路到底对不对。
结果功力果然还是不够,还是搞出了很多问题没有解决。但又想到了某些东西。
首先是思路的问题,刚才尝试在草稿纸上面演算了一下,发现这个演算时候的过程有点像解数学题目,刚开始的时候还是不太具体,所以忽略了一些条件,导致具体的思路上还是有问题,然后没有解决又继续接着做下去了。
但如果把解决数学题目的思路来做的话,可以这样想,首先需要把全部条件列举出来,比如我们还是想按照原本的思路,那么具有的条件也就是 row, col, 边界, 输出元素n, 移动位置等。
有这些条件之后,就需要将所有条件组合起来,构成一个处理的程序步骤。比如之前就一致遗忘了 边界 这一条件,所以缺少条件的算法必然是有问题的。
而这样缺少条件继续往下做的话,必然会导致实现的步骤有误。所以在草稿纸演算的时候可以尝试将解题中用到的条件勾一下,然后记得回看哪一个条件没有用过,至少尝试避免缺少条件的问题。
同时将条件在草稿纸上尝试串联时,就可以发现判断边界以及移动位置上这一部分想不到一个合适的方式串联起来。到底应该怎么判断边界,是判断边界之后移动位置然后输出,还是输出之后判断边界再移动位置。
因为当时一个很主要的问题就在于移动边界后会导致又判断为上一个边界,导致无限循环错误。所以当时就像要不要记录当前位置,然后以当前下标移动下一个位置,再去输出。
但是这样的话就有其他的问题,比如说那么怎么移动下一个位置,是按照当前的位置判断是哪一个边界后移动,在下一个位置输出。但这样完全没有解决判断为边界然后错误移动位置的问题。
所以可以在草稿纸上看出,通过将条件列举并串联成过程的话,可以在这种复杂问题上先踩坑,如果在具体文字的算法都模糊不清,那么具体实现的时候就不要决定能够给出正确的解决办法。
然后是在具体的实现的过程中,发现解决的过程可以继续的拆解。我们上面说到了这个螺旋可以看成是打印图案的思路。那么在解决的时候可以不要将遍历图案以及输出元素结合起来,应该先能够将这个图案的遍历正确跑一边,然后再想着将元素输出进去。
比如可以另外开一个测试的程序,然后模拟一个同样的二维数组,往里面输出标记,看看自己是否能够以给定的顺序跑一遍这个图案。正确后再想着把这个序列输出进去。
但很显然我们连这个图案都没有正确顺序地跑出来,就别提什么输出元素了。白搭。
还有调试中遇到的其他的一些问题,当时想初始化这个二维数字,发现用 int a[m][n]{0}; 的方式初始化不干净。不晓得为什么,然后用了 fill() 结果按照给出变量名称,然后加上元素个数的方式发现错误了。正确的写法是下面:
fill(a[0], a[0] + m * n, 0);
要指向它的二级地址后再加上元素个数才正确。因为平时一位数组的话,直接给出变量名都是最底层的地址了,可以直接加上元素个数。
二维地址分行和列的话,就有一级二级的区分,并且虽然是二维但是地址再内存存放还是线性的。但是如果指向二级的列而直接加上元素个数的话,那么就会变成在行的基础上移动地址了,如果有这里的 m = 4 行,那么有12个元素就移动到12行了,直接超出地址了。
所以要指向二维的列,以最底层的元素来加上元素个数移动地址。
这里的 sort 因为是非递增所以实际是递减的顺序。而递减放在这个 sort 函数里面要加一个 greater() 函数。
而当时记错写成默认的了,默认的是 less() ,是小到大排序。而这个名称的大和小说到不是向后的序列是逐渐增大和减小,而是只向前,首位的元素是逐渐增大还是减小。
有点反直觉。通常都是自然顺序向后的,他给了一个逆序向前描述。
大概先记录这么多,在同一题上花费太多时间,效率有点迷。看见这个题目都烦了。以后还是掐个表,免得同一道题花费太多时间。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号