【高数小笔记】一道微分运算在微分方程中的应用

　　最近在复习高数，感觉学校里某些老师讲的依托答辩，果然大学还是得靠自学-_-

　　偶然从书上发现的一道不错的题：

　　

 

 　　我就按我的思路细嗦一下：

　　首先，这看起来并不常规，因为我们发现了这个项，而这个项所代表的含义则是x关于y的二阶导。我们常见的是形式是这种，而做一道题就是要将不熟悉的内容转化为自己所熟悉的内容，因此我们可以从微分运算的角度建立这两者的联系。

　　我们熟知：y对x的二阶导其实就是y'对x的一阶导，因此我们就有：

　　

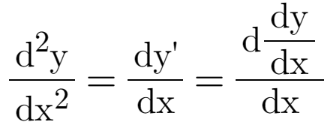
 　　相应的，把上式的y与x调换一下，就变成了题目中的形式：

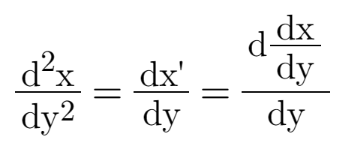　　......(1)

　　这看起来是不是稍微亲切一些了，因为我们将难以运算的二阶导（d^2/dy^2）转化成了易于运算的一阶导(d/dy)，为什么这样就易于运算呢？因为显然：

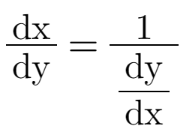    ............(2)

 　　这是处理反函数导数的常用方法，需要熟练运用。

 　　我们将(2)式代入(1):

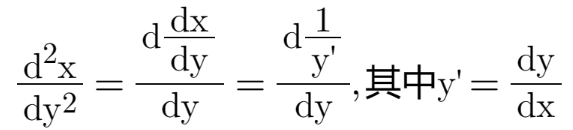　　.......(3)

 　　下面，我们只需要处理这个奇奇怪怪的东西即可。

　　因为y=y(x)，也即y是x的函数，因此我们可以从求导的方式来帮助我们运算微分，参考下面的计算：

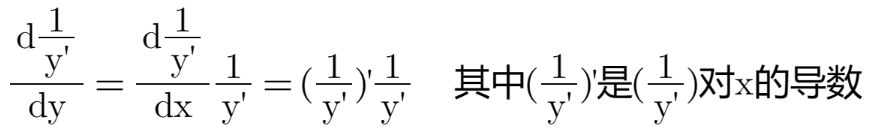　　........(4)

 　　然后，我们只需要计算(1/y')'即可，就用我们常用的分式求导公式吧：

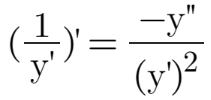　　........(5)

　 把(1)~(5)式联立起来，我们就很容易知道这坨奇奇怪怪的玩意是什么啦！

 　　然后就是一些基础的化简，没啥难度也就不细嗦了。

　　补个答案：，顺便放一下课堂ppt给的步骤（不好评价）