正睿20NOIp前冲刺day7

估分：100+100+40=240

实际：70+100+40=210

T1:

　　无中生有的特判没判

　　1沙子可以转换成b/a铅，1铅可以转换成d/c金，1金可以转换成f/e沙子，所以1沙子就可以转换成(b*d*f)/(a*c*e)沙子，看一下他能不能无限生沙子就行了

 1 #include<cstdio>
 2 #include<cstring>
 3 #include<iostream>
 4 #include<algorithm>
 5 using namespace std;
 6 
 7 int main()
 8 {
 9     int T;
10     scanf("%d", &T);
11     while (T--)
12     {
13         int a, b, c, d, e, f;
14         scanf("%d%d%d%d%d%d", &a, &b, &c, &d, &e, &f);
15         if ((c == 0 && d) || (a == 0 && b && d)) { puts("MEI"); continue; }
16         puts((b * d * f) > (a * c * e) ? "MEI" : "FON");
17     }
18 }
View Code

T2:

　　倒序遍历操作，若是一操作就操作他该操作的次数，若是二操作就把l~r区间的操作的操作次数都增加该操作的操作次数次，相当于区间修改套区间修改。

 1 #include<cstdio>
 2 #include<cstring>
 3 #include<iostream>
 4 #include<algorithm>
 5 using namespace std;
 6 
 7 typedef long long LL;
 8 
 9 const int N = 100010;
10 const int mod = 1e9 + 7;
11 
12 int n, m;
13 int a[N], s[N];
14 int op[N], L[N], R[N];
15 
16 int main()
17 {
18     scanf("%d%d", &n, &m);
19     for (int i = 1; i <= m; i++) scanf("%d%d%d", &op[i], &L[i], &R[i]);
20 
21     s[m] = 1;
22     int sum = 0;
23     for (int i = m; i; i--)
24     {
25         sum = (sum + s[i]) % mod;
26         if (op[i] == 2) s[R[i]] = (s[R[i]] + sum) % mod, s[L[i] - 1] = ((s[L[i] - 1] - sum) % mod + mod) % mod;
27         else a[L[i]] = (a[L[i]] + sum) % mod, a[R[i] + 1] = ((a[R[i] + 1] - sum) % mod + mod) % mod;
28     }
29 
30     sum = 0;
31     for (int i = 1; i <= n; i++)
32     {
33         sum = (LL)(sum + a[i]) % mod;
34         printf("%d ", sum);
35     }
36 }
View Code

T3：

　　只会40pts

　　nk可以看做是把k个不同的小球放进n个不同盒子里的方案数，因为每个球能放进n个盒子中的任意一个，所以方案数就是nk，所以我们可以把nk转换成

　　

 

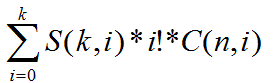
 　　（S(k,i)表示第二类斯特林数）

　　所以我们就可以推出下面这个式子

　　

　　　　　　　　   

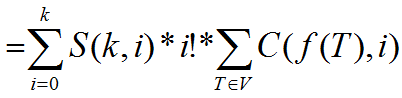
　　（T表示点集）

　　因为k是知道的，所以求后面的C(f(T),i)就行了，C(f(T),i)相当于从T的诱导子图中选i条边的方案数，设f(T)=m=i，m的端点的点集是w，所以从T的诱导子图中选i条边的方案数就等于f(T)=i的情况数*2n-w，因为只要满足f(T)=i，那么除了w之外的点随便选都行。

　　之后我们就可以分类讨论k=1/2/3了，具体在代码里（求f(T)=i的情况数是重点）

  1 #include<cstdio>
  2 #include<cstring>
  3 #include<iostream>
  4 #include<algorithm>
  5 using namespace std;
  6 
  7 typedef long long LL;
  8 
  9 const int N = 100010;
 10 const LL mod = 1e9 + 7;
 11 
 12 int n, m, K;
 13 int A[N], B[N];
 14 LL din[N];
 15 
 16 struct Force
 17 {
 18     int ans;
 19     bool st[N], vis[N];
 20     int h[N], num[N << 1], nex[N << 1], dqx;
 21 
 22     void init()
 23     {
 24         memset(h, -1, sizeof(h));
 25     }
 26 
 27     inline void add(int a, int b)
 28     {
 29         num[dqx] = b;
 30         nex[dqx] = h[a];
 31         h[a] = dqx++;
 32     }
 33 
 34     inline int qpow(int a, int k, int mod)
 35     {
 36         int res = 1;
 37         while (k)
 38         {
 39             if (k & 1) res = (LL)res * a % mod;
 40             a = (LL)a * a % mod;
 41             k >>= 1;
 42         }
 43         return res;
 44     }
 45 
 46     void dfs(int u, int pa)
 47     {
 48         vis[u] = true;
 49         for (int i = h[u]; ~i; i = nex[i])
 50         {
 51             int j = num[i];
 52             if (!st[j]) continue;
 53             ans++;
 54             if (vis[u]) continue;
 55             dfs(j, u);
 56         }
 57         st[u] = false;
 58     }
 59 
 60     inline int get(int sta)
 61     {
 62         ans = 0;
 63         memset(st, 0, sizeof(st));
 64         memset(vis, 0, sizeof(vis));
 65         for (int i = 1; i <= n; i++)
 66         {
 67             if ((sta >> (i - 1)) & 1)
 68             {
 69                 st[i] = true;
 70             }
 71         }
 72 
 73         for (int i = 1; i <= n; i++) if (st[i]) dfs(i, 0);
 74         return ans;
 75     }
 76 }F;
 77 
 78 struct Solve1
 79 {
 80     int solve()
 81     {
 82         return (LL)F.qpow(2, n - 2, mod) * m % mod;
 83     }
 84 }K1;
 85 
 86 struct Solve2
 87 {
 88     int solve()
 89     {
 90         LL res = 0;
 91         for (int i = 1; i <= n; i++) res = (LL)(res + din[i] * (din[i] - 1) % mod) % mod;
 92 
 93         LL ans = 0;
 94         ans = (LL)m * F.qpow(2, n - 2, mod) % mod;
 95         ans = (LL)(ans + res * F.qpow(2, n - 3, mod) % mod) % mod;
 96 
 97         res = (((LL)m * (m - 1) % mod - res) % mod + mod) % mod;
 98         ans = (LL)(ans + res * F.qpow(2, n - 4, mod) % mod) % mod;
 99         return ans;
100     }
101 }K2;
102 
103 struct Solve
104 {
105     int vis[N];
106     int h[N], num[N << 1], nex[N << 1], dqx;
107 
108     void add(int a, int b)
109     {
110         num[dqx] = b;
111         nex[dqx] = h[a];
112         h[a] = dqx++;
113     }
114 
115     bool cmpd(int x, int y) { return din[x] == din[y] ? x > y:din[x] > din[y]; }
116 
117     int cir3()
118     {
119         int res = 0;
120         dqx = 0;
121         memset(h, -1, sizeof(h));
122         for (int i = 1; i <= m; i++)
123             cmpd(A[i], B[i]) ? add(A[i], B[i]) : add(B[i], A[i]);
124         for (int i = 1; i <= n; i++)
125         {
126             for (int j = h[i]; ~j; j = nex[j]) vis[num[j]] = i;
127             for (int j = h[i]; ~j; j = nex[j])
128             {
129                 int v = num[j];
130                 for (int k = h[v]; ~k; k = nex[k])
131                     if (vis[num[k]] == i) res++;
132             }
133         }
134         return res;
135     }
136 
137     int solve()
138     {
139         int ans = (K1.solve() + 3ll * (K2.solve() - K1.solve() + mod)) % mod;
140         int s1 = 1ll * m * (m - 1) * (m - 2) % mod, s2 = 1ll * cir3() * 6 % mod, s3 = 0, s4 = 0, s5 = 0;
141         for (int i = 1; i <= n; i++)
142             s4 = (s4 + 1ll * din[i] * (din[i] - 1) * (din[i] - 2)) % mod;
143         for (int i = 1; i <= m; i++)
144         {
145             int u = A[i], v = B[i];
146             s5 = (s5 + 6ll * (din[u] - 1) * (din[v] - 1)) % mod;
147         }
148         s5 = (s5 - 3ll * s2 % mod + mod) % mod;
149         for (int i = 1; i <= n; i++)
150             s3 = (s3 + 3ll * din[i] * (din[i] - 1) * (m - 2)) % mod;
151         s3 = (s3 - (3ll * (s2 + s4) + 2ll * s5) % mod) % mod;
152         s1 = (s1 - 1ll * (s2 + s3 + s4 + s5) % mod + mod) % mod;
153         ans = (ans + 1ll * s2 * F.qpow(2, n - 3, mod) + 1ll * (s4 + s5) * F.qpow(2, n - 4, mod) + 1ll * s1 * F.qpow(2, n - 6, mod) + 1ll * s3 * F.qpow(2, n - 5, mod)) % mod;
154         return ans;
155     }
156 }K3;
157 
158 int main()
159 {
160     scanf("%d%d%d", &n, &m, &K);
161 
162     if (n <= 15)
163     {
164         F.init();
165 
166         for (int i = 1; i <= m; i++)
167         {
168             int a, b;
169             scanf("%d%d", &a, &b);
170             F.add(a, b), F.add(b, a);
171         }
172 
173         LL res = 0;
174         for (int i = 0; i < (1 << n); i++)
175         {
176             res = (LL)(res + F.qpow(F.get(i), K, mod)) % mod;
177         }
178         printf("%lld\n", res);
179     }
180     else if (K == 1)
181     {
182         for (int i = 1, a, b; i <= m; i++) scanf("%d%d", &a, &b);
183         printf("%d", K1.solve());
184     }
185     else if (K == 2)
186     {
187         for (int i = 1; i <= m; i++)
188         {
189             int a, b;
190             scanf("%d%d", &a, &b);
191             din[a]++, din[b]++;
192         }
193         
194         printf("%d", K2.solve());
195     }
196     else
197     {
198         for (int i = 1; i <= m; i++)
199         {
200             int a, b;
201             scanf("%d%d", &a, &b);
202             A[i] = a, B[i] = b;
203             din[a]++, din[b]++;
204         }
205         printf("%d", K3.solve());
206     }
207 }
View Code

 

总结：

　　简单题还是要多看一下，题简单肯定有坑。关于数学的东西还是欠缺，特别是类似于求和求积的公式不会推，要多补一下数学。

posted on 2020-10-20 17:26  ArrogHie  阅读(165)  评论(0)    收藏  举报

博客园  ©  2004-2025
浙公网安备 33010602011771号 浙ICP备2021040463号-3