正睿十一A班模拟赛day1

 

估分：25+0+60=85

实际：25+0+60=85

T1：

　　就只会25的暴力

　　分治，到一个区间[l,r]，cnt[i]表示i这个颜色在区间内的出现次数，从两头同时扫描，扫描到第一个cnt[i]小于f[r-l+1]后往下走，先继续搜较大的区间，再搜索小区间，返回时把cnt清空，因为已经搜过了就没必要搜了

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;

const int N = 1000010;

int n;
int c[N], f[N], cnt[N];

int ans;

void dfs(int l, int r)
{
    for (int i = l, j = r; i <= j; i++, j--)
    {
        if (cnt[c[i]] < f[r - l + 1])
        {
            for (int k = l; k <= i; k++) cnt[c[k]]--;
            dfs(i + 1, r);
            for (int k = l; k < i; k++) cnt[c[k]]++;
            dfs(l, i - 1);
            return;
        }
        if (cnt[c[j]] < f[r - l + 1])
        {
            for (int k = r; k >= j; k--) cnt[c[k]]--;
            dfs(l, j - 1);
            for (int k = r; k > j; k--) cnt[c[k]]++;
            dfs(j + 1, r);
            return;
        }
    }

    ans = max(ans, r - l + 1);
    for (int i = l; i <= r; i++) cnt[c[i]]--;
}

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) scanf("%d", &c[i]), cnt[c[i]]++;
    for (int i = 1; i <= n; i++) scanf("%d", &f[i]);
    dfs(1, n);
    printf("%d", ans);
}

 

T2：

　　可能有个10分的暴力，但没写完

 　　看见环就copy一遍，然后从每个位置剖开字符串得到n个长为n的字符串，把这些字符串排个序，前k小的字符串是从哪剖的答案就是什么了，再特判一下全相等的情况（因为这个方法不会排长度，所以其实可能能把他卡掉）

#include<cstdio>
#include<cstring>
#include<vector>
#include<iostream>
#include<algorithm>
using namespace std;

#define pb push_back

const int N = 2010;

int n;
int id[N];
string str, s[N];

bool cmp(int a, int b)
{
    return s[a - 1] < s[b - 1];
}

bool cmp1(string a, string b)
{
    return a < b;
}

int main()
{
    cin >> str;
    n = str.size();
    int k;
    scanf("%d", &k);

    bool flag = true;
    for (int i = 1; i < n; i++)
    {
        if (str[i] != str[i - 1]) flag = false;
    }
    if (flag)
    {
        int t = n / k;
        int res = n % k;
        for (int i = 1; i <= n; i += t)
        {
            printf("%d ", i);
            if (res) i++, res--;
        }
        return 0;
    }

    str += str;
    for (int i = 0; i < n; i++)
    {
        s[i].assign(str, i, n);
        id[i] = i + 1;
    }
    sort(id, id + n, cmp);
    sort(s, s + n, cmp1);

    vector<int> ans;
    for (int i = 0; i < k; i++) ans.pb(id[i]);
    sort(ans.begin(), ans.end());
    for (auto i : ans) printf("%d ", i);
}

 

T3：

　　因为有一个k的宽容，经过简单的推理过程就能得出答案至少为n-1，60分就到手了，若n=9,构造就这样

　　0 1 2 3 4 5 6 7 8

　　8 7 6 5 4 2 1 0 3

　　a正序，b逆序，把b[n/2+1]挪到最后

 

　　正解：

　　当n=4k+2或n=4k+3时就是上面的构造方法，不存在答案为n的构造，证明如下：
　　

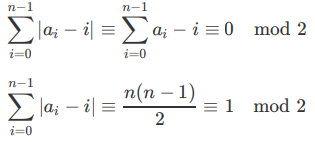
 　　当n=4k时，设构造出的排序为a，我们把a_i和i连边，就会得到下面这样的环：

　　

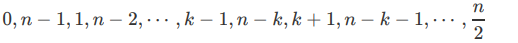
 　　当n=4k+1时，可以得到这样的环：

　　

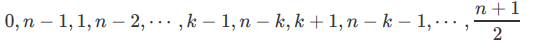
 　　可以看出a_i,和b_i的差值都是不同的

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;

const int N = 1000010;

int n, k;
int t1, t2, p[N], sz;
char c[10];

void write(int x) 
{
    if (x < 0) putchar('-'), x = -x;
    if (x / 10) write(x / 10);
    putchar(x % 10 + '0');
}

int main()
{
    scanf("%d%d", &n, &k);
    t1 = 1, t2 = n;

    if ((n & 3) > 1)
    {
        for (int i = 1; i <= (n >> 1); ++i)
        {
            p[t1] = t2;
            p[t2] = t1 + 1;
            t1++, t2--;
        }
        p[t1] = 1;
    }
    else
    {
        for (int i = 1; t1 < t2; ++i) 
        {
            p[t1] = t2;
            if (t1 == (n >> 2)) p[t1 + 1] = t1 + 1, ++t1;
            p[t2] = t1 + 1, ++t1, --t2;
        }
        p[t1] = 1;
    }
    for (int i = 1; i <= n; ++i) write(i - 1), putchar(' ');
    puts("");
    for (int i = 1; i <= n; ++i) write(p[i] - 1), putchar(' ');
}