Ark__Skadi

HDU 2196 Computer（树形dp）

题面转送门

经典树形dp例题

观察题目，发现对于树上某一节点，其答案分为如下两部分：

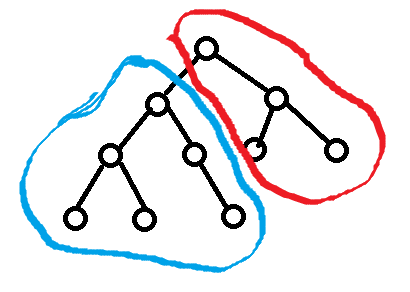
蓝色部分是以节点i为根的子树，红色部分是以父节点为根的不含i及其子树的子树

对于蓝色部分，我们可以在dfs时由子节点汇总求得,记为len[i][0]

代码：

 1 void dfs(int u,int f)
 2 {
 3     for(int i=head[u];i;i=edge[i].next)
 4     {
 5         int v=edge[i].to;
 6         if(v==f) continue;
 7         dfs(v,u);
 8         if(len[v][0]+edge[i].w>len[u][0])                
 9             len[u][0]=len[v][0]+edge[i].w;
10 //        cout<<u<<' '<<v<<' '<<edge[i].w<<endl;
11     }
12 }

在求完蓝色部分后，我们来着手求红色部分

红色部分的特点是，以父节点为根的子树内最大值不一定在红色区域内，即最大值形成的路径可能穿过目前的点i

对此，我们的应对方法是，计算次大值，记为len[i][1]

代码：

 1 void dfs(int u,int f)
 2 {
 3     for(int i=head[u];i;i=edge[i].next)
 4     {
 5         int v=edge[i].to;
 6         if(v==f) continue;
 7         dfs(v,u);
 8         if(len[v][0]+edge[i].w>len[u][0])
 9         {                
10             len[u][1]=len[u][0];
11             len[u][0]=len[v][0]+edge[i].w;
12         }
13         else if(len[v][0]+edge[i].w>len[u][1])
14             len[u][1]=len[v][0]+edge[i].w;
15 //        cout<<u<<' '<<v<<' '<<edge[i].w<<endl;
16     }
17 }

 

最终，我们还要记录以i为根的子树最大值来自于以谁为根的子树，记在fr数组中

即在修改时加上

fr[u]=v;

最后，将从父节点转移过来的值记在len[i][2]中

状态转移方程是：
len[u][2]=w+max(len[f][0],len[f][2])[u!=fr[f]]

len[u][2]=w+max(len[f][1],len[f][2])[u==fr[f]]

全代码：

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 int n;
 4 struct node{
 5     int next;
 6     int to;
 7     int w;
 8 }edge[20005];
 9 int cnt,head[10005],sum,len[10005][3],fr[10005];
10 void add(int u,int v,int w)
11 {
12     edge[++cnt].next=head[u];
13     edge[cnt].to=v;
14     edge[cnt].w=w;
15     head[u]=cnt;
16 }
17 void dfs(int u,int f)
18 {
19     for(int i=head[u];i;i=edge[i].next)
20     {
21         int v=edge[i].to;
22         if(v==f) continue;
23         dfs(v,u);
24         if(len[v][0]+edge[i].w>len[u][0])
25         {                
26             len[u][1]=len[u][0];
27             len[u][0]=len[v][0]+edge[i].w;
28             fr[u]=v;
29         }
30         else if(len[v][0]+edge[i].w>len[u][1])
31             len[u][1]=len[v][0]+edge[i].w;
32 //        cout<<u<<' '<<v<<' '<<edge[i].w<<endl;
33     }
34 }
35 void dfs2(int u,int f,int w)
36 {
37     if(u==fr[f])
38         len[u][2]=w+max(len[f][1],len[f][2]);
39     else
40         len[u][2]=w+max(len[f][0],len[f][2]);
41     for(int i=head[u];i;i=edge[i].next)
42     {
43         int v=edge[i].to;
44         if(v==f) continue;
45         dfs2(v,u,edge[i].w);
46     }
47 }
48 int main()
49 {
50     while(cin>>n)
51     {
52         cnt=0;
53         memset(head,0,sizeof(head));
54         memset(len,0,sizeof(len));
55         memset(fr,0,sizeof(fr));
56         memset(edge,0,sizeof(edge));
57         for(int i=2;i<=n;i++)
58         {
59             int x,y;
60             cin>>x>>y;
61             add(i,x,y);
62             add(x,i,y);
63         }
64         dfs(1,0);
65 //        for(int i=1;i<=n;i++)
66 //            cout<<len[i][1]<<endl;
67         dfs2(1,0,0);
68     //    for(int i=1;i<=n;i++)
69     //        cout<<len[i]<<endl;
70         for(int i=1;i<=n;i++)
71             cout<<max(len[i][0],len[i][2])<<endl;
72     }    
73 }
74 /*
75 7
76 1 1
77 1 2
78 2 1
79 2 1
80 3 2
81 3 2
82 */
83

 

posted on 2020-07-31 15:29  Ark__Skadi  阅读(32)  评论(0)    收藏  举报