非自回归图像描述生成｜总结

这是一个蛮有趣的领域，旨在保留大部分自回归效果的前提下，显著降低推理时间（说一下监督学习一般用“预测”这种说法，非监督学习通常是“推理”）。

Paper 1: Non-Autoregressive Coarse-to-Fine Video Captioning (2021)

这篇论文提出了Coarse-to-Fine这样一种方法。

我们都知道Transformer的Decoder是单向的，亦即从左侧向右侧预测而看不到右边，GPT正是如此。论文把Decoder改成了双向的，和BERT一样并行生成。这很能提升模型速度，但作为代价，它根本没办法保证语义连贯性。

具体怎么做呢？

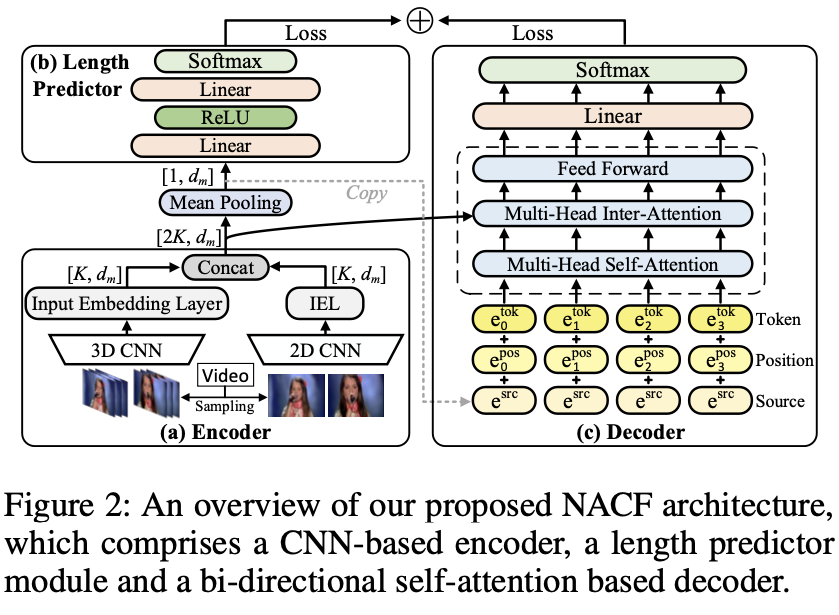
（左侧）首先对图片编码，编码后预测生成的序列长度。

由于早期图片信息提取用的是线性的CNN，所以需要额外对CNN提取的向量\(V\)作非线性变换得到\(f(V)\)送到后面步骤（后来的ViT不需要这么做）：

\[f(V)=\text{BatchNorm}(G\circ \overline{V}+(1-G)\circ \hat{V}) \]

这里的\(G\)是门控系数，根据输入的\(V\)动态决定线性变换和非线性变换的比例：

\[\begin{aligned} \overline{V}&=VW_{e1}\\ \hat{V}&=\text{tanh}(\overline{V}W_{e2})\\ G&=\sigma (\overline{V}W_{e3}) \end{aligned} \]

序列长度预测是接受图像编码器输出的\(R\)，针对同一个视频，统计真实的字幕长度分布，然后将预测的分布与其作KL散度损失函数的训练：

\[L=\text{Softmax}(\text{ReLU}(\text{MeanPooling}(R)W_{l1})W_{l2}) \]

\[\mathcal{L}_{len}=D_{KL}(L^*||L)=-\sum_{j=1}^{N_{max}}l^*_j \log{\frac{l_j}{l_j^*}} \]

（右侧）分成两步，第一步生成句子模版，第二步往模版填词。这两步都复用前文提到的同一个双向Decoder。

有趣的是，这个Decoder额外在输入的地方把图像Encoder的输出\(R\)拼接到Decoder的输入\(Y_{obs}\)，然后在交叉注意力的地方又把Encoder的输出再结合算一遍。这也是由于双向解码缺乏的逻辑性，需要靠输入增强来缓解。对于训练时遮掩的\(Y_{mask}\)，模型需要通过能看到的\(Y_{obs}\)把它们预测出来：

\[\mathcal L_{mlm}=-\sum_{y\in Y_{mask}}\log p_\theta (y|Y_{obs},R) \]

（右侧第一步）论文定义了一种叫“视觉词”的概念，也就是有价值的名词或动词（is，are这就是没有价值的词）。

\[y_n^{vis}=\begin{cases} y^*_n&\text{if POS}(y_n^*)\in\{\text{noun, verb}\}\\ [mask]&\text{otherwise} \end{cases} \]

最开始Decoder是看不到\(Y_{obs}\)的，所以置空：

\[L_{vis}=-\sum_{y\in Y^{vis}}\log p_\theta (y|\varnothing_{[vis]},R) \]

到此，完整的损失函数是：

\[\mathcal L_{\text{NACF}}=\mathcal L_{len}+\mathcal L_{mlm}+\lambda \mathcal L_{vis} \]

（右侧第二步）已经有句子模版“coarse”了，这个步骤是把它“fine”的过程。论文提出了三种填词的策略：Mask-Predict，Easy-First和Left-to-Right。

在第二步开始前，已经得到了包括mask和视觉词的\(y_n\)序列和对应的置信度\(c_n\)：

\[y_n^{(0)},c_n^{(0)}=(\text{arg})\mathop{\text{max}}_{w} p_\theta(y=w|\varnothing_{[vis]},R) \]

Mask-Predict方法是每一次迭代都遮蔽置信度最低的token，让Decoder重新预测它们；Easy-First每次选择置信度最高的 token填充，不会重新预测，计算量更小；Left-to-Right和Easy-First相似，区别在于从左向右仿照自回归方法填词。

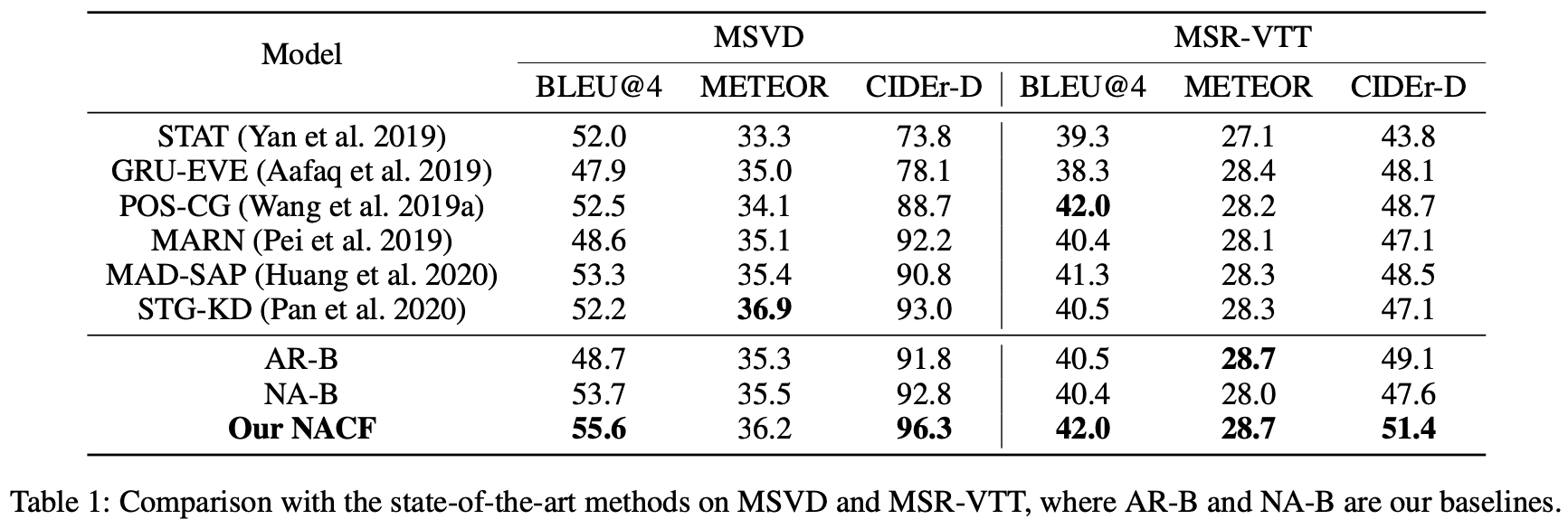
实验结果如下：