机器学习 -> Machine Learning (II)

这次来学习深度学习吧!

1 训练前

1.1 神经元与神经网络

神经元是神经网络的基本单位, 模拟了生物神经元的工作机制. 每个神经元接受一组输入, 将这些输入与其权重相乘, 然后对所有的乘积求和, 并加上一个偏置. 最后, 将得到的结果传递给激活函数.

神经网络由多个神经元组成, 这些神经元按层次结构排列: 输入层, 一个或多个隐藏层和输出层. 神经网络可以学习从输入到输出的映射, 这通常涉及大量的数据和迭代训练.

不加说明时, 普通的神经网络指的是多层感知机 MLP (Multi-Layer Perceptron). 有的被称作前馈神经网络 FNN (Feedforward Neural Network).

1.2 激活函数

是一个非线性函数, 用于确定神经元的输出. 由于激活函数的非线性特性, 多层神经网络能够捕捉并学习非线性关系. 常见的激活函数包括:

  1. ReLU
  2. Sigmoid
  3. Softmax
  4. Tanh

1.3 层

输入层是神经网络的第一层, 负责接收特征数据.

输出层是神经网络的最后一层, 负责生成最终的预测或分类结果.

在输入层和输出层之间的层都被称为隐藏层. 这些层的神经元执行计算, 可以有多个隐藏层.

全连接层 (dense) 是一种特殊的隐藏层, 指的是每一个神经元与前一层的所有神经元都连接. MLP 采用的就是全连接层.

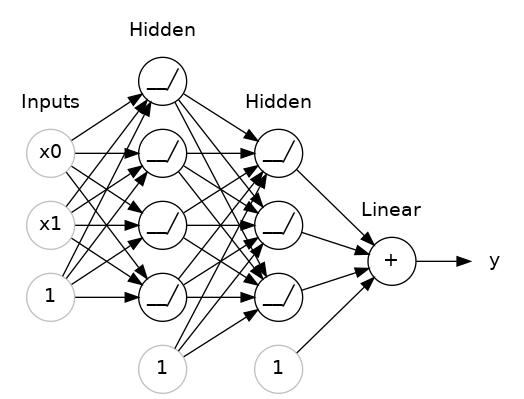
图中每个神经元的每个连接代表一个参数, 输入值会与这些参数相乘. 整个过程中经过了三次主要的计算.

1.4 损失函数与优化器

也称为代价函数或目标函数, 损失函数量化模型预测的结果与实际标签之间的差异. 它为模型提供了一个明确的反馈, 告诉模型它的预测有多差. 常见的损失函数包括:

  1. 均方误差
  2. 交叉熵
  3. Hinge Loss

反向传播 (Backward Propagation) 是一种从输出结果开始, 逐层向前计算损失函数关于每个权重的偏导数的算法.

将梯度下降法作为优化器的策略为

\[w_i^*=w_i-\alpha\frac{\partial L}{\partial w_i} \]

这里的 \(w_i\) 是某个权重, \(\alpha\) 是学习率, \(L\) 是关于各个权重的损失函数.

除此之外, 优化器还有随机梯度下降, Momentum, Adam, RMSProp, Adagrad 等方法.

1.5 批次, 轮次与迭代

批次 (Batch) 是数据集的一个子集, 用于在模型上进行一次前向和后向传播.

轮次 (Epoch) 是整个数据集完整地通过神经网络一次的过程.

迭代 (Step / Iteration) 通常是指模型在一个批次上的一次前向和后向传播.

如果数据集有 1000 个样本, 且选择的批次大小为 100, 则每个轮次需要 10 次迭代.

这些需要手动设定并可能影响模型的训练效率和最终性能的参数称为超参数. 它们一般不会自行改变.

2 训练中

2.1 过拟合

过拟合通常意味着模型已经学习到了训练数据的 "噪声" 或特定 "偏差", 而不仅仅是泛化的, 潜在的模式.

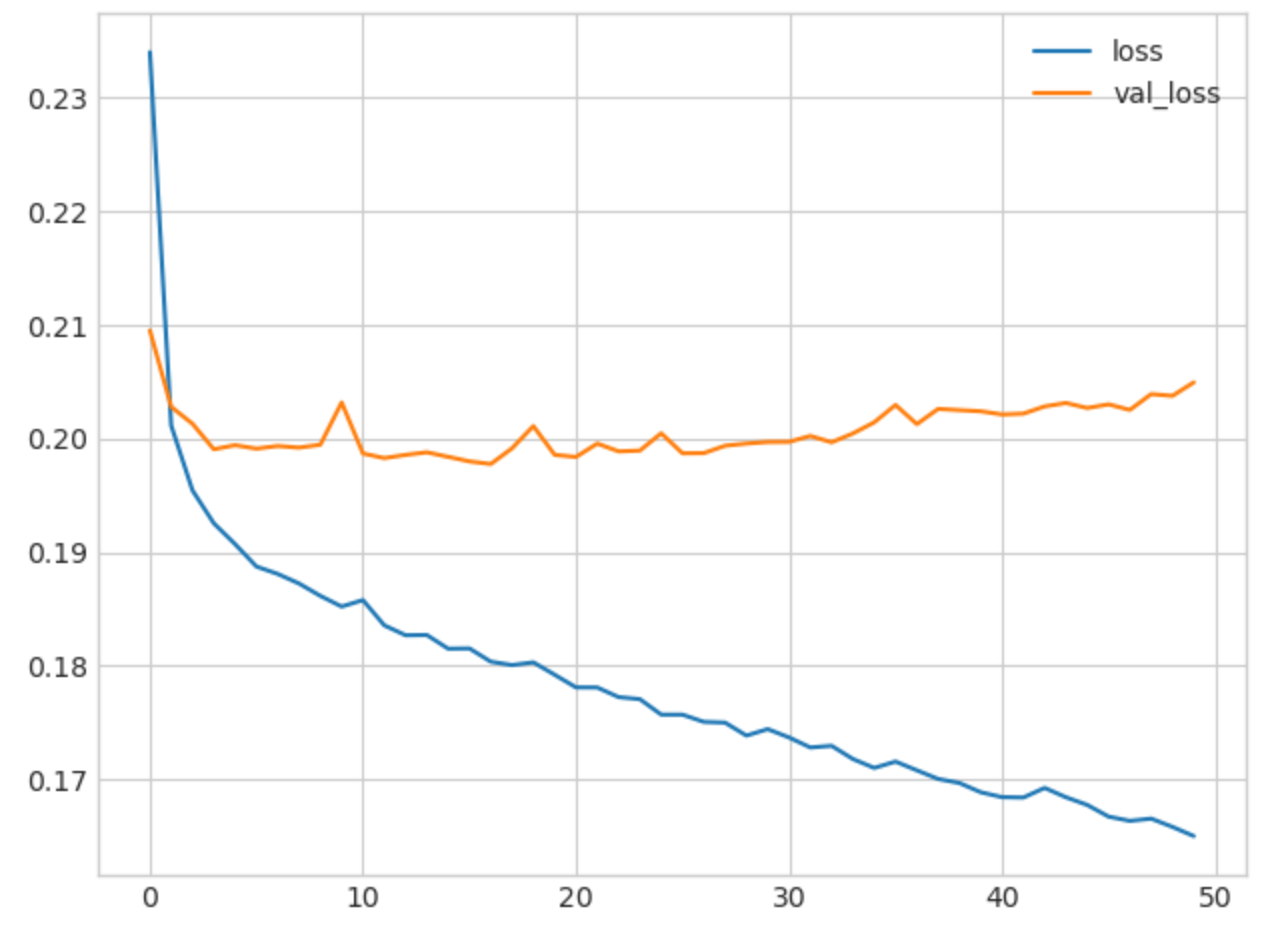
如图, 像这种损失函数变化缓慢甚至不减反增的情况表明出现了过拟合, 通常采用提前终止的方法.

early_stopping = callbacks.EarlyStopping(
    min_delta=0.001, # minimium amount of change to count as an improvement
    patience=5, # how many epochs to wait before stopping
    restore_best_weights=True,
)

2.2 随机失活与批标准化

Dropout 是一种正则化技巧, 其在训练过程中随机 "丢弃" 神经元, 从而减少过拟合.

layers.Dropout(rate=0.3)

Batch Normalization 用于规范化前一层的输出, 使其具有近似的均值和方差, 以便提高训练的稳定性, 这可以应对数据复杂收敛值过大的情况.

layers.BatchNormalization()

3 例子

3.1 二分类

Hotel Cancellations 
import pandas as pd

from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler, OneHotEncoder
from sklearn.impute import SimpleImputer
from sklearn.pipeline import make_pipeline
from sklearn.compose import make_column_transformer

hotel = pd.read_csv('../input/dl-course-data/hotel.csv')

X = hotel.copy()
y = X.pop('is_canceled')

X['arrival_date_month'] = \
    X['arrival_date_month'].map(
        {'January':1, 'February': 2, 'March':3,
         'April':4, 'May':5, 'June':6, 'July':7,
         'August':8, 'September':9, 'October':10,
         'November':11, 'December':12}
    )

features_num = [
    "lead_time", "arrival_date_week_number",
    "arrival_date_day_of_month", "stays_in_weekend_nights",
    "stays_in_week_nights", "adults", "children", "babies",
    "is_repeated_guest", "previous_cancellations",
    "previous_bookings_not_canceled", "required_car_parking_spaces",
    "total_of_special_requests", "adr",
]
features_cat = [
    "hotel", "arrival_date_month", "meal",
    "market_segment", "distribution_channel",
    "reserved_room_type", "deposit_type", "customer_type",
]

transformer_num = make_pipeline(
    SimpleImputer(strategy="constant"), # there are a few missing values
    StandardScaler(),
)
transformer_cat = make_pipeline(
    SimpleImputer(strategy="constant", fill_value="NA"),
    OneHotEncoder(handle_unknown='ignore'),
)

preprocessor = make_column_transformer(
    (transformer_num, features_num),
    (transformer_cat, features_cat),
)

# stratify - make sure classes are evenlly represented across splits
X_train, X_valid, y_train, y_valid = \
    train_test_split(X, y, stratify=y, train_size=0.75)

X_train = preprocessor.fit_transform(X_train)
X_valid = preprocessor.transform(X_valid)

input_shape = [X_train.shape[1]]

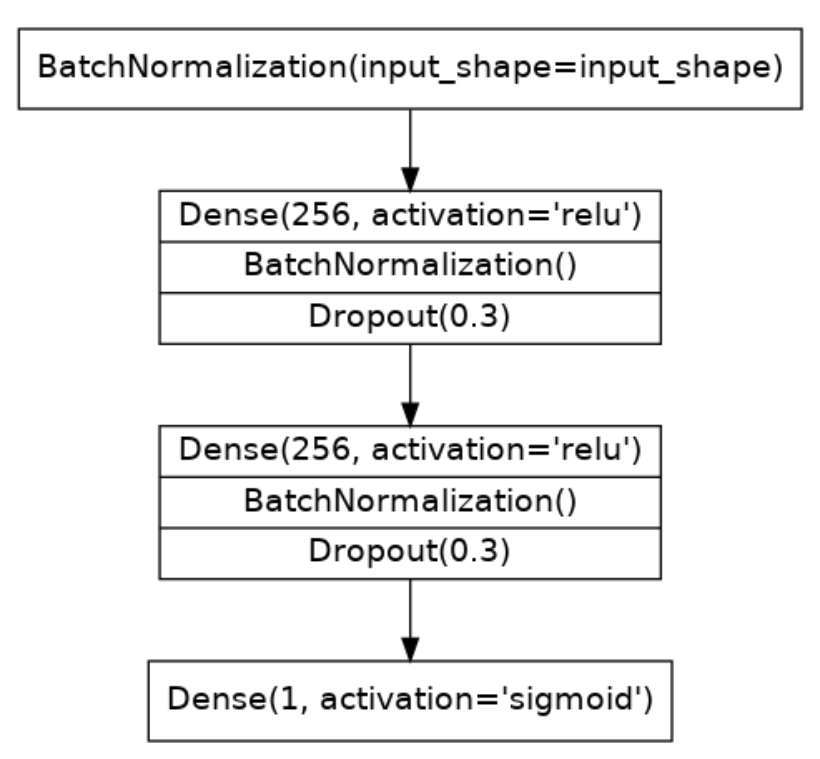
在这个例子中, 定义了一个输入层, 两个隐藏层, 一个输出层.

构建层

model = keras.Sequential([
    layers.BatchNormalization(input_shape=input_shape),
    layers.Dense(256, activation='relu'),
    layers.BatchNormalization(),
    layers.Dropout(rate=0.3),
    layers.Dense(256, activation='relu'),    
    layers.BatchNormalization(),
    layers.Dropout(rate=0.3),
    layers.Dense(1, activation='sigmoid'),
])

构建损失函数与优化器

model.compile(
    optimizer='adam',
    loss='binary_crossentropy',
    metrics=['binary_accuracy'],
)

训练

early_stopping = keras.callbacks.EarlyStopping(
    patience=5,
    min_delta=0.001,
    restore_best_weights=True,
)
history = model.fit(
    X_train, y_train,
    validation_data=(X_valid, y_valid),
    batch_size=512,
    epochs=200,
    callbacks=[early_stopping],
)
history_df = pd.DataFrame(history.history)
history_df.loc[:, ['loss', 'val_loss']].plot(title="Cross-entropy")
history_df.loc[:, ['binary_accuracy', 'val_binary_accuracy']].plot(title="Accuracy")

4 深度神经网络

前文所述的神经网络由于层数较少, 被称为 "浅层网络", 现在随着计算能力的增加出现了 DNN (Deep Neural Network) 这种 "深层网络".

DNN 特指有足够的深度以致不能简单地被视为 "浅层" 网络的网络, 具有相当多的参数.

5 卷积神经网络

CNN (Convolutional Neural Network) 的核心思想是通过多个卷积层来局部感知输入数据的特征, 并通过子采样或池化层来减少数据的空间尺寸. 它是一种专门为处理具有空间或时间连续性的数据 (如图像) 而设计的模型.

5.1 卷积运算

数学上的卷积被定义为

\[(f*g)(t)=\int_{-\infty}^{+\infty}f(\tau)g(t-\tau)\text d\tau \]

直观地说, 卷积的运算可以被看作一个函数在另一个函数上的 "滑动". 不严谨地说, 卷积是一种加权求和.

5.2 卷积操作

局部感知

与传统的全连接层相比, 卷积层的神经元只与输入数据的一个局部区域相连接, 这称为感受野. 这种局部连接的好处是可以检测到输入数据中的局部特征.

权值共享

在一个卷积层中, 每一个神经元使用相同的权重, 这称为一个卷积核或滤波器. 这种权重共享结构可以大大减少模型的参数数量, 并且可以在整个输入空间中检测到相同的特征.

卷积核

卷积核的大小是在设计卷积神经网络时确定的一个超参数. 卷积核的大小直接决定了该层神经元的感受野大小.

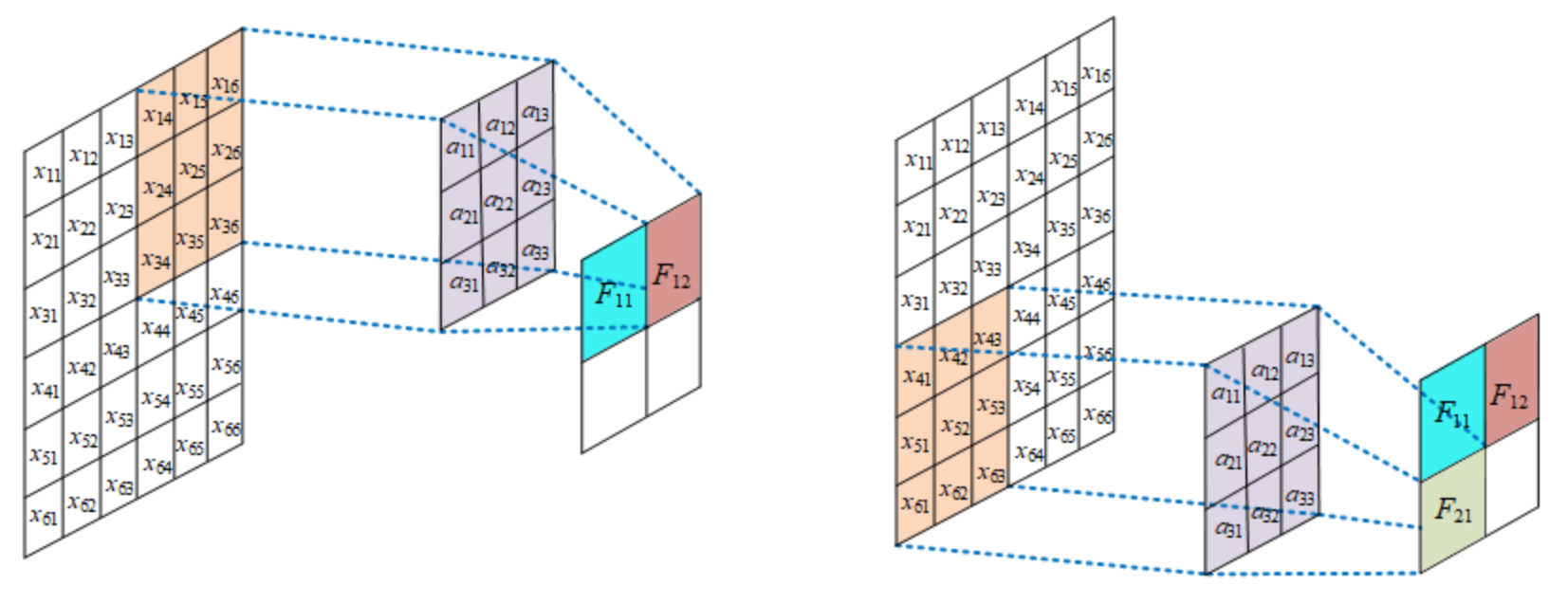
如图, 左边的是输入数据的一部分, 中间的是卷积核, 右边得到的是特征图.

5.3 池化层

在卷积层之后, 还可以通过池化层来降低卷积层输出的特征图的维度.

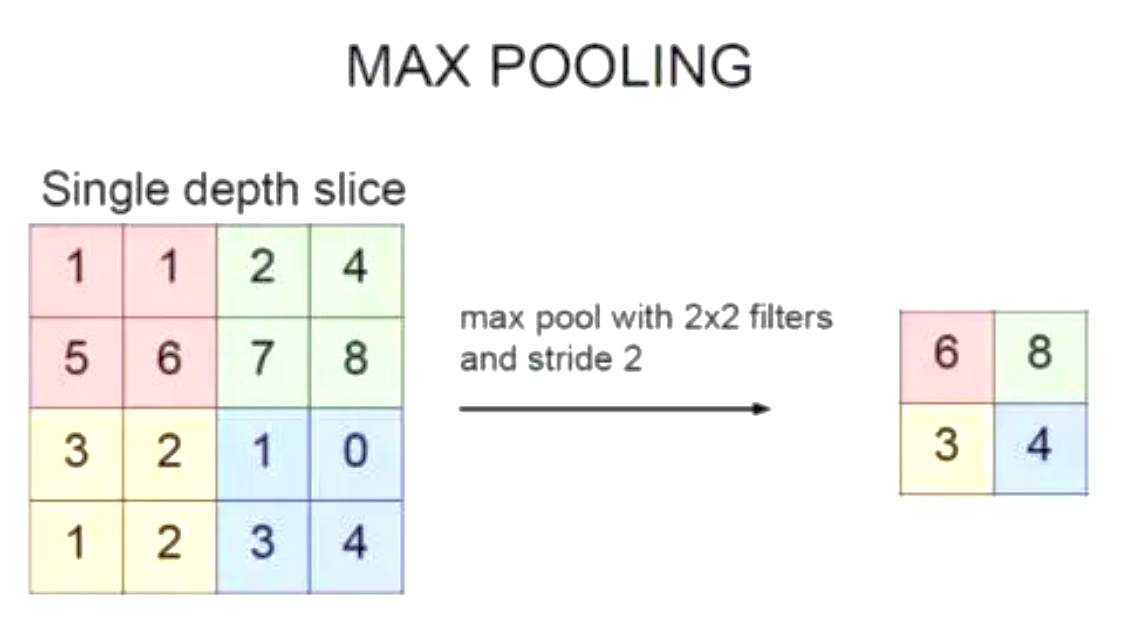
如图常采用最大池化的操作.

6 循环神经网络

RNN (Recurrent Neural Network) 的核心思想是具有 "记忆" 的能力, 它可以保存先前时间步的信息, 并在当前时间步使用. 它是一种专门为处理顺序性数据 (如序列) 而设计的模型.

6.1 结构与原理

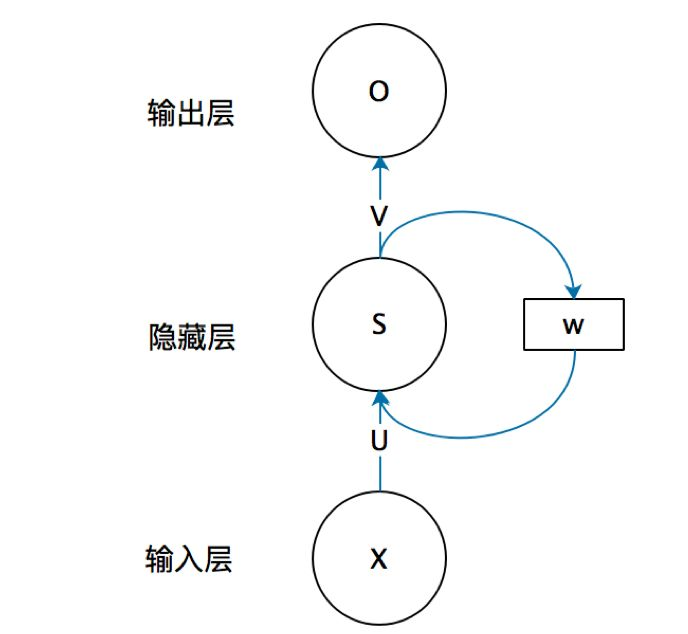
如图, 循环神经网络的隐藏层的值 \(s\) 不仅仅取决于当前这次的输入 \(x\), 还取决于上一次隐藏层的值 \(s\). 权重矩阵 \(w\) 就是隐藏层上一次的值作为这一次的输入的权重.

6.2 数学模型

\[h_t=\sigma(W_{hh}h_{t-1}+W_{xh}x_t+b_h) \]

这里, \(h_t\) 是时间 \(t\) 的隐藏状态 (隐藏层的输出), \(x_t\) 是输入. \(W_{hh}\) 和 \(W_{xh}\) 是权重矩阵, \(b_h\) 是隐藏层的偏置, \(\sigma\) 是激活函数.

对于多层 RNN, 下一层的输入是本层的 \(h_t\).

6.3 训练和梯度问题

在 RNN 中, 为了得到某一时间步的输出, 我们需要考虑所有先前的时间步. 这意味着梯度必须通过所有这些时间步进行反向传播. 如果序列很长, 那么在反向传播过程中就会涉及大量的连续的矩阵乘法. 这容易导致梯度消失 (如果值小于 1) 或梯度爆炸 (如果值大于 1).

对于梯度爆炸, 一种常见的解决方法是梯度剪裁, 设定梯度的最大值. 但梯度消失更难处理, 这就是 LSTM 和 GRU 这样的更先进的结构被引入的原因.

7 长短时记忆网络和门控循环单元

7.1 LSTM

LSTM (Long Short Term Memory) 是一种 RNN 变种, 它首先使用遗忘门来丢弃不必要的信息, 接着用输入门筛选并加入新的信息到单元状态中, 最后通过输出门决定基于当前单元状态的隐藏状态输出.

LSTM 的步骤和操作:

  1. 遗忘门 \(f_t\)

\[f_t = \sigma(W_f \cdot [h_{t-1}, x_t] + b_f) \]

  1. 输入门 \(i_t\)

\[i_t = \sigma(W_i \cdot [h_{t-1}, x_t] + b_i) \]

  1. 单元状态候选值 \(\tilde{C_t}\)

\[\tilde{C_t} = \tanh(W_C \cdot [h_{t-1}, x_t] + b_C) \]

  1. 更新单元状态 \(C_t\)

\[C_t = f_t \times C_{t-1} + i_t \times \tilde{C_t} \]

  1. 输出门 \(o_t\)

\[o_t = \sigma(W_o \cdot [h_{t-1}, x_t] + b_o) \]

  1. 隐藏状态输出 \(h_t\)

\[h_t = o_t \times \tanh(C_t) \]

  • 为什么要引入单元状态 \(C_t\) 呢?

这是因为 \(C_t\) 的更新是基于加法的, 而不是传统 RNN 中 \(h_t\) 的乘法. 加法操作对梯度的传播更为友好, 因为它避免了连续的矩阵乘法可能导致的梯度消失. 这也是为什么 \(h_t\) 被称为 "短期记忆", 而 \(C_t\) 被称为 "长期记忆".

  • 为什么用 \(h_t\) 作为输出呢?

这是因为向下一层提供 \(h_t\) 可以更加关注当前时间步的活跃信息, 而不是整个历史 \(C_t\) 的累积信息.

7.2 GRU

LSTM 有很多变体, 其中较大改动的是 GRU (Gate Recurrent Unit).

GRU 通过其更新门和重置门来权衡旧的隐藏状态和新输入的信息, 从而生成新的隐藏状态.

GRU 的步骤和操作:

  1. 更新门 \(z_t\)

\[z_t=\sigma(W_z\cdot[h_{t-1},x_t]) \]

  1. 重置门 \(r_t\)

\[r_t=\sigma(W_r\cdot[h_{t-1},x_t]) \]

  1. 新的提议隐藏状态 \(h'_t\)

\[h'_t=\tanh(W\cdot[r_t\times h_{t-1},x_t]) \]

  1. 隐藏状态的最终更新 \(h_t\)

\[h_t=(1-z_t)\times h_{t-1}+z_t\times h'_t \]

  • 这是如何解决梯度消失问题的?

GRU 通过更新门来决定历史隐藏状态的哪些部分应当被保留, 更新门相当于把遗忘门和输入门结合在一起了. 其实本质上 GRU 和 LSTM 都是因为做了矩阵加法导致不容易梯度消失.

8 注意力机制

传统的序列模型如 RNN 或 LSTM, 处理序列时是按照固定的顺序, 一步接一步. 这导致处理长序列时存在挑战. 注意力机制的提出就是为了解决这个问题, 它允许模型在决定输出时, 能够 "关注" 输入序列中的不同部分.

8.1 自注意力机制

自注意力机制 (SA) 是 Transformer (变换器) 的核心机制.

\[\text{Attention}(Q,K,V)=\text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V \]

其中 \(Q,K,V\) 分别是 query, key, value 向量, 每一组 \((Q,K,V)\) 是由一个输入数据与三个权重矩阵的乘积得到的.

\(\sqrt{d_k}\) 是为了缩放的因子, 其中 \(d_k\) 是 key 的维度.

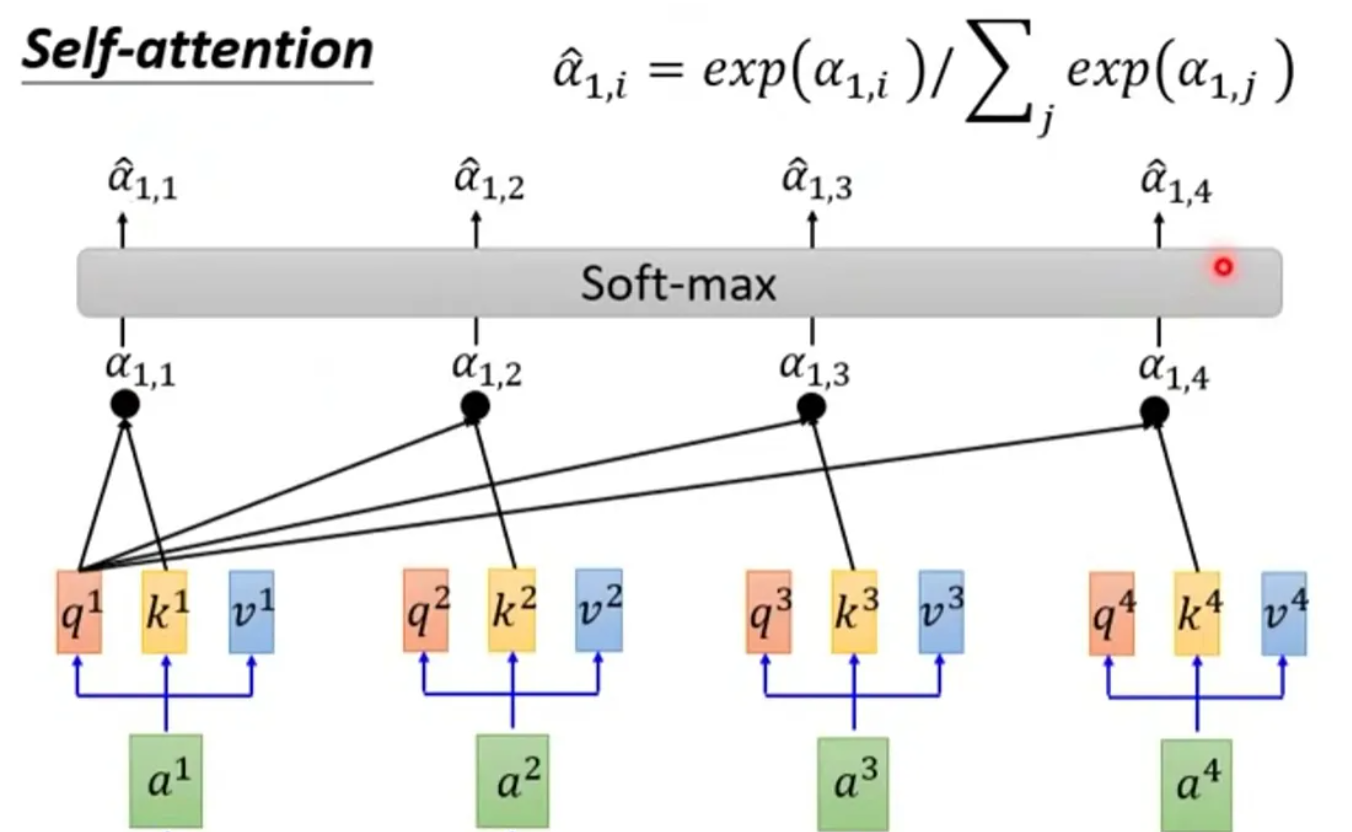
  • 这个式子是什么意思呢?

首先, 对于给定的 Query (Q), 我们要计算其与所有 Key (K) 的相似度. 这通常通过取 Q 和每个 K 的点积来完成, 计算得到一个分数.

然后, 为了确保这些分数可以被合理地解释为权重, 我们使用 softmax 函数进行归一化.

最后, 我们使用上面计算出的权重来对 Value (V) 进行加权求和. 结果越大说明注意力越高.

  • 为什么已经有了 key 用于匹配查询, 还要用 value 表示信息含量呢?

打个比方. 某些词 (如 the, is, of 等) 可能经常出现并与许多查询匹配, 但它们本身可能不携带太多特定的语义信息. 这种情况 Keys 可能与许多 Queries 有高匹配度, 但其 Values 可能不会为最终的输出提供太多有价值的信息.

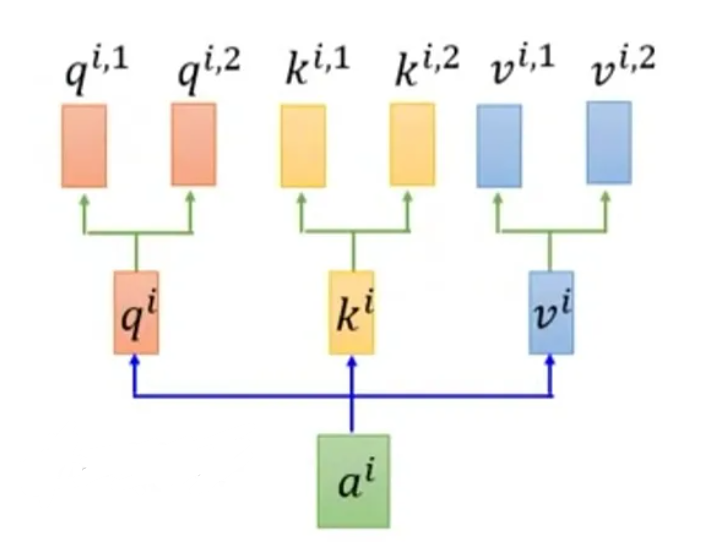
8.2 多头注意力机制

多头注意力机制 (MH) 通过使用多个独立的注意力头, 分别计算注意力权重, 并将它们的结果进行拼接或加权求和, 从而获得更丰富的表示.

8.3 导向注意力机制

导向注意力机制 (GA) 使用一个模态来 "指导" 另一个模态的注意力.

GA 和 SA 基本相似, 只不过将图像看作是提供 key 和 value 的来源, 而文本 (在 VQA 任务中通常是问题) 作为提供 query 的来源.

8.4 协同注意力机制

模块化协同注意力机制 (MCA) 是一种特殊的协同注意力机制 (CA), 目的是将 SA 和 GA 结合在一起, 有以下三种形式:

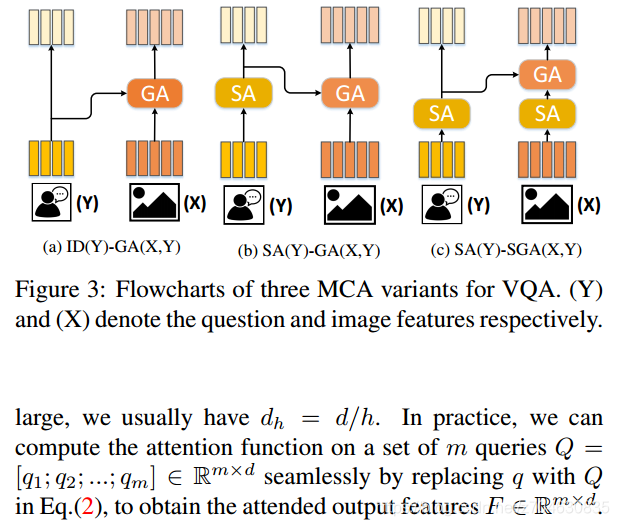
其中 ID 表示返回自身的身份函数, SA, GA 和 SGA 都可以被视为函数, 它们处理输入并返回注意力处理后的输出.

MCAN 网络正是由这些 MCA 层构成的. 在得到很多个 MCA 层输出的文本和图像特征后, 采用简单的 MLP 就可以得到分类结果.

posted @ 2023-08-29 14:37  rainrzk  阅读(94)  评论(0)    收藏  举报