换根DP学习笔记
换根DP
简述
换根DP是一类特殊的树形DP。比较难想到, 但是理解了就不难了(指思路, 不是指题).
在解题过程中,存在一类树上问题,要求我们求解每个节点做为根节点的时的一些数据的问题。朴素算法一般是\(O(n^2)\)地进行n次dfs。遇到这种问题时,我们可以通过考察根节点转移到相邻节点时的影响,从而得出状态转移方程,进而\(O(1)\)地转移根节点得到新的答案。最后达到将问题总的复杂度降到\(O(n)\)的目的。
问题引入
给定一棵n个节点无向树(n个节点,n-1条无向边的连通图),要求选出一个节点,使得该节点做为根节点时,所有节点的深度和最大。
某个节点的深度被定义为 该节点与根节点的距离。
我们不难想到用dfs在\(O(n)\)的时间内求出任一给定节点做为根节点时, 所有节点的深度和. 因此容易想到一个朴素的算法是进行n次dfs, 时间复杂度\(O(n^2)\).
朴素算法是可行的, 但我们并不满足.
使用换根DP可以将时间复杂度降到\(O(n)\).
问题分析
让我们钦定选定一号节点做为根节点.
让\(size_i\)表示以第i个节点为根节点的子树大小.(一号节点做为根节点的意义下)
让\(dp_i\)表示第i个节点做为根节点时的所有节点的深度和.
记节点\(u\) 为节点\(v\)的 (一号节点做为根节点的意义下的)父节点.
那么可以得到状态转移方程\(dp_v = dp_u-size_v+(size_1-size_v)\)
第一个\(-size_v\)的意义是, 当根节点转移到节点v之后, 以节点v为根节点的子树的所有节点的深度都减一. (因为节点u是节点v的父节点)
第二个\(size_1-size_v\)的数量意义是, 总节点数减去以v为根节点的子树的大小. 在方程中的意义是, 所有不是以节点v为根节点的子树的节点的深度加一. (离根节点更远了)
不难看出这个方程的边界条件是\(dp_1\).
得到状态转移方程之后, 我们只需要dfs预处理一遍出所需要的信息(比如\(size\)数组, 比如\(dp_1\))即可, 再dfs一次出所有的答案取最大值即可.
代码
/* 换根DP 模板题 */
#include <algorithm>
#include <vector>
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 1e6+10;
vector<int> G[N];
void add(int u, int v)
{
G[u].push_back(v);
G[v].push_back(u);
}
int n;
int sz[N];
int dep[N];
int maxx;
LL f[N];
void pre(int u, int fa) //预处理深度和子树大小
{
sz[u] = 1;
for(int v: G[u])
{
if(v == fa) continue;
dep[v] = dep[u]+1;
pre(v, u);
f[1] += dep[v];
sz[u] += sz[v];
}
}
void dp(int u, int fa)
{
for(int v: G[u])
{
if(v == fa) continue;
f[v] = f[u] - 2*sz[v] + sz[1]; //状态转移方程
dp(v, u);
}
if(f[u] > f[maxx]) maxx = u;
}
int main()
{
scanf("%d",&n);
for(int i = 1; i < n; i++)
{
int u, v; scanf("%d %d",&u,&v);
add(u, v);
}
//建图
maxx = 1;
pre(1, 0); //预处理
dp(1, 0); //DP
cout << maxx << endl;
system("pause");
}
例题分析:
[USACO10MAR]Great Cow Gathering G
只是上面那题加了边权, 点权而已, 不能说一模一样, 只能说完全相似.
直接给出状态转移方程 \(f[v] = f[u] + (sz[1] - 2*sz[v])*w;\) 其中w是边权, 节点u是节点v的父节点, \(sz[i]\)表示以节点i为根节点的子树大小.
note: 边权和size相乘时会爆int
#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;
typedef long long LL;
const int N = 1e5+100;
struct edge{
int to, w;
};
vector<edge> G[N];
void add(int u, int v, int w)
{
G[u].push_back({v, w});
G[v].push_back({u, w});
}
int n;
LL c[N];
LL f[N];
LL sz[N];
void pre(int u, int fa)
{
sz[u] = c[u];
for(auto x: G[u])
{
if(x.to == fa) continue;
pre(x.to, u);
sz[u] += sz[x.to];
f[u] += sz[x.to] * x.w + f[x.to];
}
}
LL ans;
void dp(int u, int fa)
{
for(auto x: G[u])
{
if(x.to == fa) continue;
f[x.to] = f[u] + (sz[1] - 2*sz[x.to])*x.w;
dp(x.to, u);
}
if(f[u] < ans) ans = f[u];
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i++) cin >> c[i];
for(int i = 1; i < n; i++)
{
int u, v , w; cin >> u >> v >> w;
add(u, v, w);
}
ans = 1ll<<62;
pre(1, 0);
dp(1, 0);
cout << ans << endl;
// system("pause");
}
[USACO12FEB]Nearby Cows G
乍看起来很恐怖, 但是考虑到\(k\le20\)就可以直接暴力了. 复杂度\(O(kn)\)
记\(f[i][j]\)为离节点\(i\)的距离为\(j\)的节点的数量.
第一次dfs预处理下\(f[i][j]\), 让其等于其本身定义, 但只限定在以节点i为根的子树中.
给出第二次dfs状态转移方程: \(f[v][j] += \sum_{cnt=2}^{k}f[u][cnt-1] - f[v][cnt-2]\)
#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;
typedef long long LL;
const int N = 1e5+100;
vector<int> G[N];
void add(int u, int v)
{
G[u].push_back(v);
G[v].push_back(u);
}
LL c[N];
LL f[N][22];
int n, k;
void pre(int u, int fa)
{
f[u][0] = c[u];
for(int v: G[u])
{
if(v == fa) continue;
pre(v,u);
for(int i = 0; i < k; i++)
f[u][i+1] += f[v][i];
}
}
void dfs(int u, int fa)
{
for(int v: G[u])
{
if(v == fa) continue;
for(int i = k; i >= 2; i--)
{
f[v][i] += f[u][i-1] - f[v][i-2];
}
f[v][1]+=c[u];
dfs(v, u);
}
}
int main()
{
cin >> n >> k;
for(int i = 1; i < n; i++)
{
int u, v; cin >> u >> v;
add(u, v);
}
for(int i = 1; i <= n; i++) cin >> c[i];
pre(1, 0);
dfs(1, 0);
for(int i = 1; i <= n; i++)
{
LL ans = 0;
for(int j = 0; j <= k; j++)
ans += f[i][j];
cout << ans << endl;
}
// system("pause");
}
CF708C Centroids
简要题干:
给定一棵无根树,共n个节点。
允许进行一次操作:选择一条边,并将这条边删除,然后再新加一条边。操作必须保证执行完后依然是棵树。
删除哪条边和增加一条新边是完全自由的。
问,有多少节点在执行完一次或零次操作之后可以变成树的重心。
其中,树的重心等价于,将该节点删除后,剩下的森林没有任何树的大小大于\(\lfloor\frac{n}{2}\rfloor\).
数据规模:\(n\le 4e5\)
分析:
记以节点v为根的子树的大小为\(sz[v]\)。
首先给出性质:一棵树一定有重心。
既然是无根树,我们不妨指定一个原树的重心做为根节点。
这样做的好处是,根据重心的定义,对于任意非根节点\(x\), 必然存在$sz[x] \le \frac{n}{2} $.
于是对于任意一个非根节点\(x\),我们只要考虑其父节点的这个子树。
如果其父节点这个子树大于\(\frac{n}{2}\), 那么我们就应该从这个父节点子树中找出一个子树\(target\),使得\(n-sz[x]-sz[target]\le \frac{n}{2}\).
如下图所示:
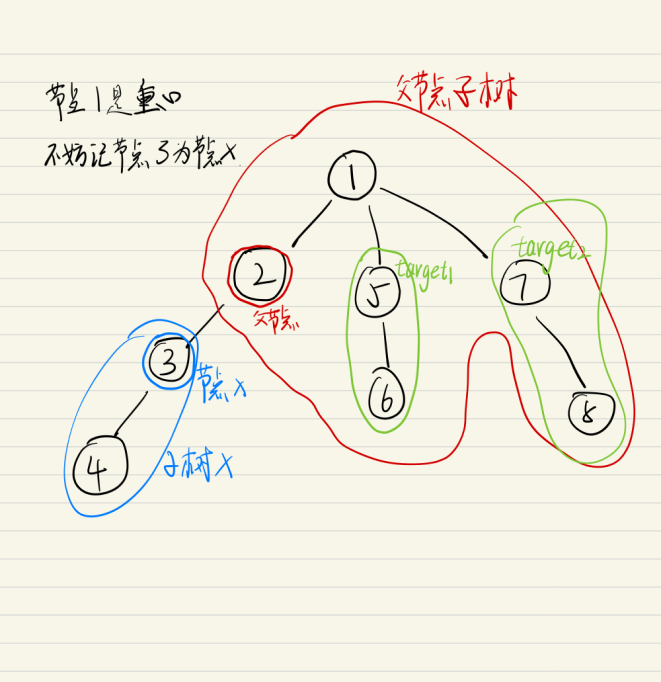
也就是说,我们现在把问题转化成了,对于每个非根节点\(x\),我们要在 原树减去以节点x为根的子树的树中 找到一个不超过\(\frac{n}{2}\)的最大子树,不妨记这个子树的大小为\(f[x]\).
然后我们去check\(n-sz[x]-f[x]\le \frac{n}{2}\)。
一个直观的想法是,\(f[x] = f[fa]\), 从定义上来看这是显然的。
然后再考虑以节点x的兄弟节点为根的子树内的大小不超过\(\frac{n}{2}\)。
不妨设节点x的兄弟节点集合为\(B(x)\), 记以节点v为根的子树的不超过\(\frac{n}{2}\)的子树大小为\(d[j]\) 于是我们得出:
考虑上面这个柿子遇到菊图会被卡成\(O(n^2)\)的,于是我们用一个小技巧进行转换, 记\(d[i][0]\)为以节点i为根的子树的不超过\(\frac{n}{2}\)的最大子树大小, \(d[i][1]\)以节点i为根的子树的不超过\(\frac{n}{2}\)的次大子树大小:
于是本题就可做了。
三遍dfs,第一遍找重心,一次预处理\(d[],size[]\)数组,一次换根DP。
#include <iostream>
#include <algorithm>
#include <queue>
#include <cstring>
#include <map>
#include <set>
#include <cmath>
#include <assert.h>
using namespace std;
//#pragma GCC optimize(2)
#define close(); ios::sync_with_stdio(false);
#define endl '\n'
#define rep(i, l, r) for(int i = l; i <= r; i++)
#define dwn(i, r, l) for(int i = r; i >= l; i--)
typedef long long LL;
const int N = 4e5+100;
int n;
vector<int> G[N];
int root;
int f[N];
int dp[N][2];
int sz[N];
int is[N];
void pre(int x = 1, int fa = 0)
{
int mx = 0;
sz[x] = 1;
for(int e: G[x])
{
if(e == fa) continue;
pre(e, x);
mx = max(mx, sz[e]);
sz[x] += sz[e];
}
if(n - sz[x] <= n/2 && mx <= n/2 ) is[x] = 1;
}
void dfs1(int x = root, int fa = 0)
{
sz[x] = 1;
for(int e: G[x])
{
if(e == fa) continue;
dfs1(e, x);
sz[x] += sz[e];
int t = ((sz[e] <= n/2)? sz[e]: dp[e][0]);
if(t <= n/2 && dp[x][0] < t)
{
dp[x][1] = dp[x][0];
dp[x][0] = t;
}
else if(t <= n/2 && dp[x][1] < t)
{
dp[x][1] = t;
}
}
}
void dfs(int x = root, int fa = 0)
{
if(x != root)
{
f[x] = (n-sz[x]<=n/2)? n-sz[x]: 0;
int t = ((sz[x] <= n/2)? sz[x]: dp[x][0]);
if(t != dp[fa][0]) f[x] = max(dp[fa][0], f[0]);
else f[x] = max(f[x], dp[fa][1]);
f[x] = max(f[x], f[fa]);
}
else f[x] = 0;
if(f[x] >= n-n/2-sz[x]) is[x] = 1;
for(int e: G[x])
{
if(fa == e) continue;
dfs(e, x);
}
}
int main()
{
close();
cin >> n;
rep(i, 1, n-1)
{
int u, v; cin >> u >> v;
G[u].push_back(v);
G[v].push_back(u);
}
pre();
rep(i, 1, n) if(is[i]) { root = i; f[root] = dp[root][0]; break; }
dfs1();
dfs();
rep(i, 1, n) cout << is[i] << " "; cout << endl;
// system("pause");
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号