凸函数与优化

讲的比较透彻，关于凸函数的定义、性质、在优化中的优势

from: https://zhuanlan.zhihu.com/p/56876303

凸函数定义

一个函数 f:Rn→R 是一个凸函数，当且仅当以上两个条件成立：

1. 函数 f 的定义域 dom f 是一个凸集；
2. f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)   θ∈(0,1)

一个函数是严格凸函数当且仅当条件二当且仅当 x=y 时才取等号。凸函数的图像使用下图举例。

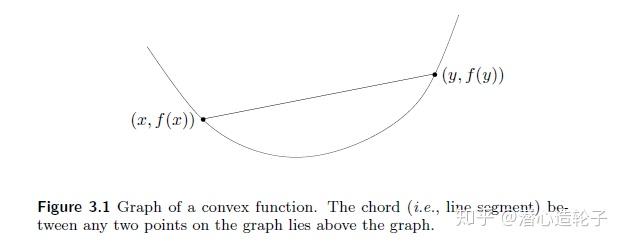
由上图来看，凸函数的几何意义在于，定义域中任意两点连线组成的线段都在这两点的函数曲线（面）上方。由凸函数的定义可以类似地引出凹函数的定义：如果函数 f 是凸函数，那么函数 −f 是凹函数。从凸函数与凹函数的定义，我们可以发现所有的仿射函数（Affine Function）即满足凸函数的性质，又满足凹函数的性质，因此是“既凸又凹”的。

我们也可以从另一个解释凸函数的定义。在上文关于凸函数的定义中，我们要求凸性对于定义域中任意两点 x,y 成立，结合凸性（条件2）的定义，我们可以发现凸性从几何上来说描述的是函数曲面（线）上任意两点间的超平面（直线）与函数曲面之间的相对关系。因此从这个角度。我们可以给出凸函数的另一个定义：

给任意x 、 v 以及 t ，如果函数 f(x) 是凸函数，当且仅当函数 g(t)=f(x+tv) 也是其定义域（ {t|x+tv∈dom f} ）内的凸函数。

这个定义在判断函数凸性时与前一个定义一样都有广泛的应用。

扩展值函数（Extended-value extensions）

在实际中，我们常常将凸函数的定义域推广至 Rn ，推广的方式是将原函数定义域以外的部分定义为 ∞ ，即：

f^(x)={f(x)    x∈dom f∞        x∉dom f

其中 f^(x) 称为扩展值函数，它定义在 Rn上。我们也可以从扩展值函数中恢复出原函数的定义域：

dom f={x|f^(x)<∞}

利用扩展值函数，我们可以简化对函数的描述，因为此时不必再描述函数的定义域。

我们很容易地可以验证扩展值函数同样适用于上述关于凸函数的定义。考虑凸性的定义：

f^(θx+(1−θ)y)≤θf^(x)+(1−θ)f^(y)   θ∈(0,1)

如果， x∈dom f 且 y∈dom f ，那么如果原函数 f 是凸函数，扩展值函数 f^(x) 也是凸函数。如果 x∈dom f 但是 y∉dom f 。由拓展函数的定义，上式右边等于无穷大，那么如果原函数 f 是凸函数，扩展值函数 f^(x) 也是凸函数。因此，我们可以说，如果一个如果原函数 f 是凸函数，那么扩展值函数 f^(x) 不改变函数的凸性。因此，为了简化对凸函数的描述，在之后的所有文章中，我们对于都默认所有的凸函数都取其对应的扩展值函数的形式，而不再对其的定义域做过多强调。

凸函数判定条件

介绍完凸函数的定义后，显然我们可以使用定义来判断一个函数时候是凸函数，事实上很多时候我们也的确是这么做的。但是，实际上关于凸函数的判定方法有更简单直观的方法。下面两小节介绍凸函数判定的一阶与二阶条件。

一阶条件

考虑一个可微函数 f ，即 f 的梯度 ∇f 在 dom f 中处处存在，函数 f 是凸函数当且仅当对于 ∀x,y∈dom f ，有下式成立：

f(y)≥f(x)+∇f(x)T(y−x)上述条件成为凸函数判定的一阶条件。一阶条件有清晰的几何意义：凸函数永远位于其切线的上方。这一点可以使用下图阐释：

进一步分析上式，可以发现 f(x)+∇f(x)T(y−x) 是函数 f 在 x 处的一阶泰勒近似，那么上述条件就说明了对于凸函数而言，其任意位置处的一阶泰勒展开总是其本身的全局下界（global under-estimator）。而泰勒展开描述的是函数 f 的局部性质，由此我们得到有关凸函数的一个重要性质：凸函数是一类可以由局部信息推导出全局信息的函数。为了解释这一点，我们考虑 ∇f(x)=0 的位置，对于凸函数 f 有， f(y)≥f(x)    ∀ x,y∈dom f ，说明 x 是函数 f 的全局最小值。而我们导出 x 是全局最小值只使用了 f(x) 的局部性质—— ∇f(x)=0 。这说明了凸函数可以“管中窥豹”的优良特性。在数学分析中，我们总是去分析函数的局部信息（微分），以此去分析函数的特性，而凸函数的这种优良特性使得我们只需要分析函数的局部性质就可以获知其全局特性，这大大简化了研究难度，因此使得凸函数与凸优化问题成为了最先受到学者广泛研究的问题。类似于条件一，我们可以给出严格凸函数与凹函数的判断条件。

二阶条件

现在我们假设函数 f 是二阶可微的，即函数 f 的Hessian矩阵在定义域内处处存在，那么函数 f 是凸函数当且仅当对于定义域内的任意一点 x ，该点处的Hessian矩阵是半正定的,即：

∇2f(x)⪰0

对于标量函数而言，Hessian矩阵半正定退化为： f″(x)≥0 ，意味着函数 f 的导函数是非递减的。从几何上来说，Hessian矩阵处处半正定意味着函数 f 处处曲率非负。

类似地，我们可以发现对于严格凸函数有 ∇2f(x)≻0 ，对于凹函数有 ∇2f(x)⪯0 。

一些常见凸函数

在本节中，我们将介绍一些常见的凸函数，我们首先从标量函数开始介绍：

1. 指数函数： eax 是 R 上的凸函数，对 ∀a∈R 。
2. 幂函数： xa 当 a≥1,or a<0 时是凸函数，当 0≤x<1 是凹函数。
3. 绝对值幂函数： |x|a 在 a≥1 时是凸函数。
4. 对数函数： log x 是凹函数。
5. 负熵函数： xlog x 是凸函数。

上面几个函数通过凸函数判定的二阶条件很容易地可以验证它们的凸性。下面介绍一些矢量凸函数：

1. 范数（Norm）：任意 Rn 上的范数函数都是凸函数（可以由范数的三角不等式结合凸函数定义得证）。
2. 最大值函数： max{x1,x2,...,xn} 是 Rn 上的凸函数。
3. Quadratic-over-linear function：例如函数 f(x,y)=x2y 就是凸函数，这一点可以通过求其Hessian矩阵验证其正定性看出，也可以从函数图像中直观看出。

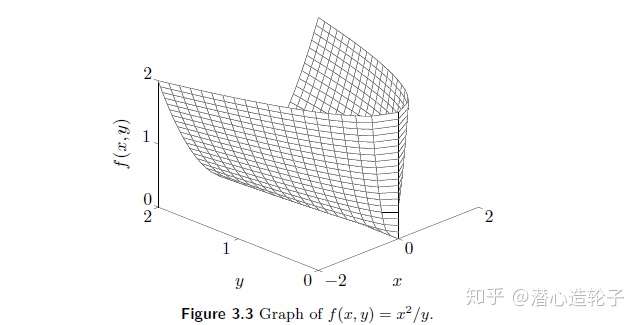
4. Log-sum-exp函数：函数 f(x)=log(ex1+ex2+ex3+...+exn) 是凸函数。该函数可以可以看出是最大值函数的可微近似：

max{x1,x2,...,xn}≤f(x)≤max{x1,x2,...,xn}+log n

对于 n=2 的情况，绘制出函数图像如下：

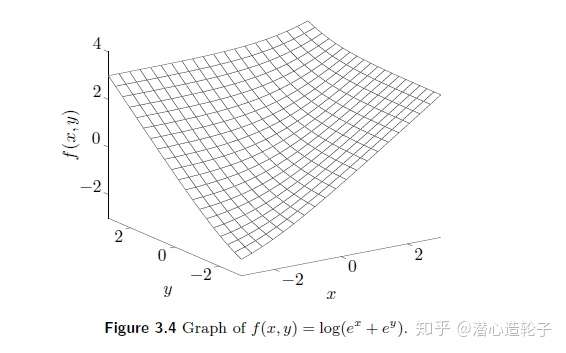
5. 几何平均函数：函数 f(x)=(∏i=1nxi)1n 是凹函数。

6. 对数行列式函数（log-determinant）：对于对称正定矩阵，函数 f(x)=log detX 是凸函数。因为 det X=∏iλi ，对于对称正定矩阵，所有特征值 λi 都是大于0的，因此 log det X=log( ∏iλi)=∑ilog λi ，由于对数函数是凸函数，其线性组合依然是凸函数（这一点在下一篇保凸运算中会有所介绍），因此 f(x)=log detX 是凸函数。

上述的矢量凸函数的凸性证明均可以在书上找到，这里不对具体的证明细节进行叙述，感兴趣的读者可以参考Convex Optimization 73-74页的证明。

子水平集（Sublevel Set）

函数 f:Rn→R 的 α -子水平集定义为：

Cα={x∈dom f|f(x)≤α}

从定义中可以看出，子水平集指的是定义域中满足对应条件的部分。一个凸函数的任意子水平集都是凸集：假设 x,y∈α−sublevel set ，因此 f(x)≤α, f(y)≤α ，因此 f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)≤θα+(1−θ)α=α ，因此 θx+(1−θ)y∈α−sublevel set 。

Epigraph

函数 f:Rn→R 的 Epigraph定义为：

epi f={(x,t)|x∈dom f,f(x)≤t}

是 Rn+1 的子集。Epigraph的定义可以由下图阐释。

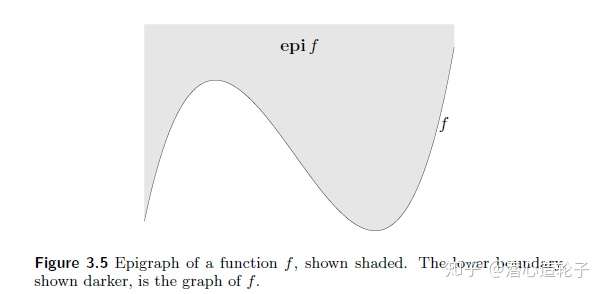
从几何上来说， epi f 可以认为是函数 f 曲面（线）以上的部分。因此，Epigraph是联系凸函数与凸集的纽带——函数 f 是凸函数当且仅当它的Epigraph是凸集。

詹森不等式及其拓展

凸函数的定义式：

f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)

又被称为詹森不等式。上面的基本詹森不等式可以被拓展为高维乃至无穷维的情况：

• 如果函数 f 是凸函数，那么对于 x1,x2,...xn∈dom f ，以及任意 ∑iθi=1,θ⪰0 ，有下式成立：

f(∑iθixi)≤∑iθif(xi)

• 如果函数 f 是凸函数，且 ∫Sp(x)dx=1 ,那么有下式成立：

f(∫Sxp(x)dx)≤∫Sp(x)f(x)dx

如果 p(x) 看作是随机矢量 x 的概率密度分布，那么上面的积分不等式可以写作下式：

f(E x)≤E f(x)

利用詹森不等式可以证明一些重要的不等式，比如Holder不等式、几何平均与算数平均关系不等式等等，这些在Convex Optimization的78页有所阐述，这里不进行仔细说明，只是对詹森不等式的形式以及它与凸函数的关系进行阐述，意在对詹森不等式有所了解。

本文介绍了凸函数的基本定义、判定方法、一些与凸函数相关的概念与常见凸函数，下一篇文章将会介绍一些保凸运算。