前缀和

前缀和

前缀和更像一个公式，理解思想之后直接套公式就可以解题。

一维前缀和

有一个数组\(a_1,a_2,a_3...\)

则前缀和数组为\(S_i = a_1 + a_2 + ... + a_i\).

• 前缀和的下标建议从1开始。这样\(S_0\)就会为0，处理边界会很方便。

例如区间和[1,5]为\(S_5-S_0=S_5\)，当\(S_0=0\)时，可以统一使用整体计算公式\(S_r-S_{l-1}\)，

从而不用进行if的边界判断。

前缀和的作用

快速求出原数组中一段数的和。

例如我们要算出数组区间[l,r]区间的和，如果对数组循环一遍，前缀和是O(n)的，在使用前缀和的情况下是O(1)的。

使用前缀和的话这段区间和就等于\(S_r-S_{l-1}\),因为\(S_r=a_1+a_2+...+a_r，而S_{l-1}=a_i+a_2+...+a_{l-r}\),

二者相减的结果正好是\(a_l+...+a_r\)。这就是前缀和最大的用处。

如何求前缀和

S[0]定义成0.

S[i] = S[i-1] + a[i].

帮助理解的题目

输入一个长度为n的整数序列。

接下来再输入m个询问，每个询问输入—对l, r。

对于每个询问，输出原序列中从第l个数到第r个数的和。

输入格式

第一行包含两个整数n和m。

第二行包含n个整数，表示整数数列。

接下来m行，每行包含两个整数l和r，表示一个询问的区间范围。

输出格式

共m行，每行输出一个询问的结果。

数据范围

1≤l≤r≤n,
1≤n,m≤100000,
-1000≤数列中元素的值≤1000

输入样例

5 3
2 1 3 6 4
1 2
1 3
2 4

输出样例

3
6
10

代码实现

import java.util.Scanner;

public class PrefixAnd{

    static Scanner scanner = new Scanner(System.in);
    static final int N = (int)1e5+10;
    static int n = scanner.nextInt();
    static int m = scanner.nextInt();
    static int[] a = new int[N];
    static int[] s = new int[N];

    public static void main(String args[]) throws Exception {
        for(int i = 1; i <= n; i++) a[i] = scanner.nextInt();
        for(int i = 1; i <= n; i++) s[i] = s[i-1] + a[i];

        while(m-- > 0)
        {
            int l=scanner.nextInt();
            int r=scanner.nextInt();
            System.out.println(s[r]-s[l-1]);
        }
    }
}

二维前缀和

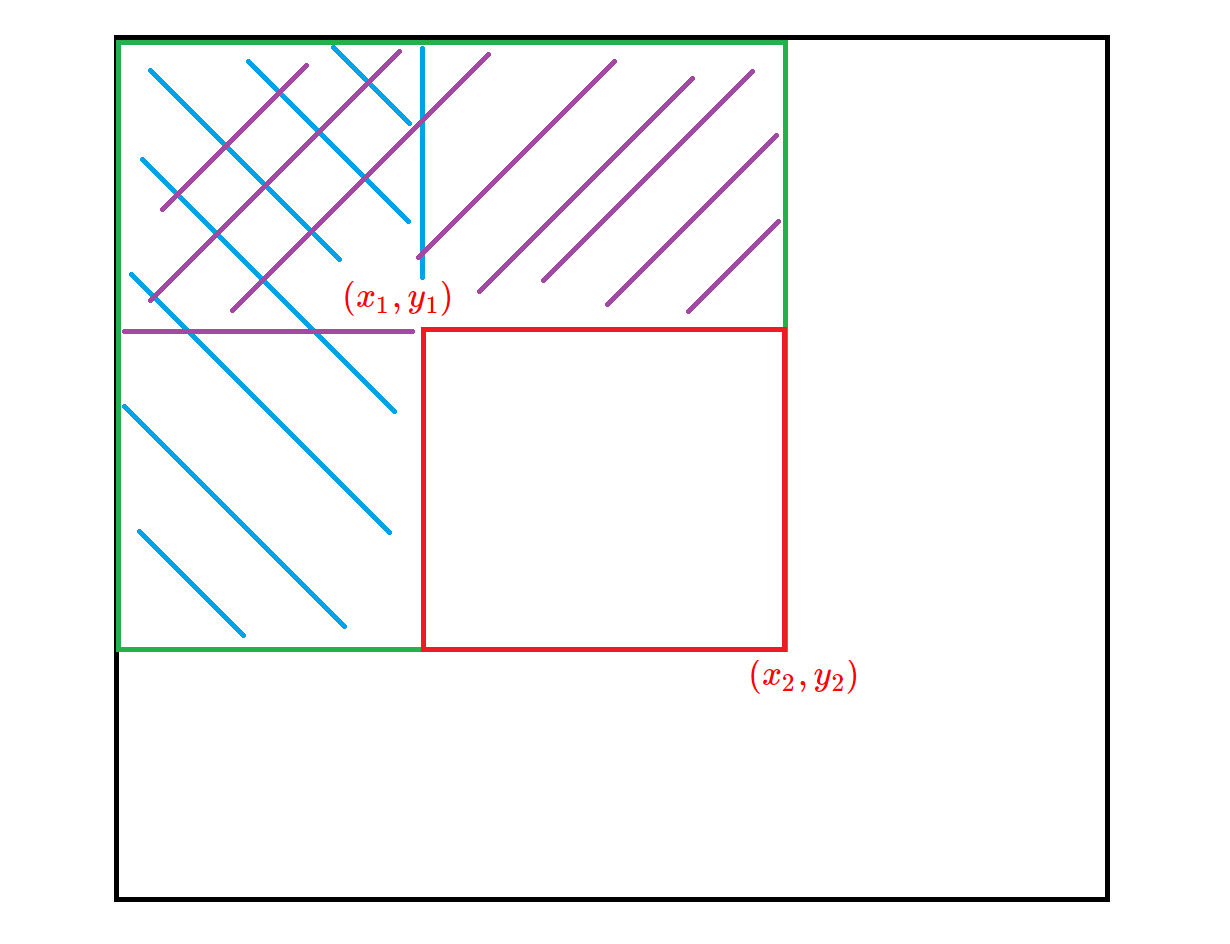
比如我们求红色矩形的面积，那么

红色矩形面积就等于绿色矩形-蓝色矩形-紫色矩形+蓝紫相交部分，即

求和 = \(S_{x_2 \enspace y_2}\) - \(S_{{x_2} \enspace {y_1}_{-1}}\) - \(S_{{x_1}_{-1} \enspace {y_2}}\) + \(S_{{x_1}_{-1} \enspace {y_1}_{-1}}\)

那么\(S_{i\enspace j}\)如何计算，也很简单，用两重循环就可以了

for(i : 1~n)
\(\enspace \enspace\)for(j : 1~m)
\(\enspace \enspace \enspace \enspace S_{i\enspace j} = S_{i-1 \enspace j} + S_{i \enspace j-1} - S_{i-1 \enspace j-1} + a_{i \enspace j}\)

这个原理也如上图，紫色+蓝色-蓝紫相见的部分，剩下的红色部分由于连续性，他就是\(a_{i \enspace j}\)
下面放一个图帮助理解：

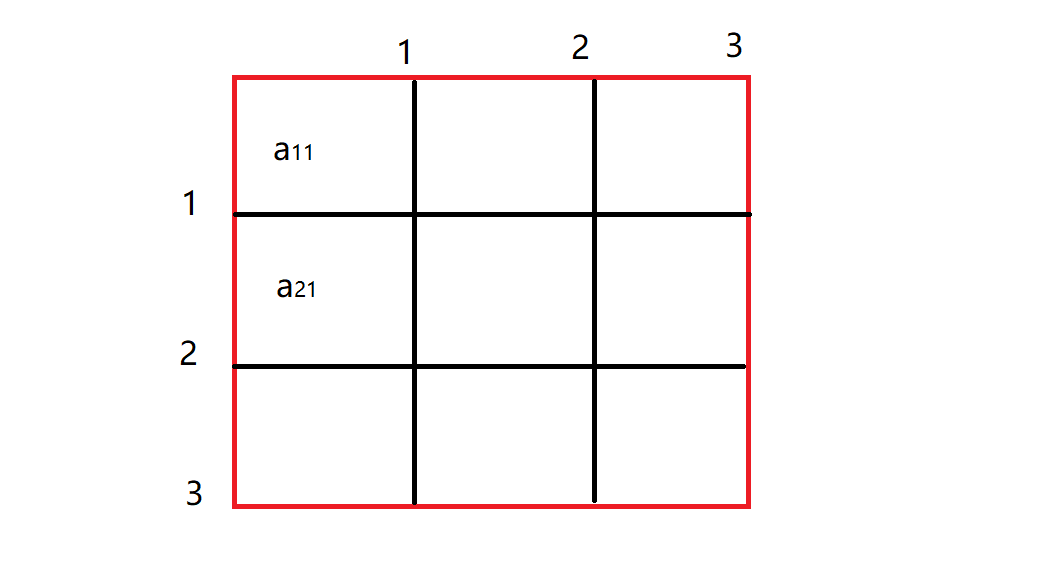
例题

输入一个n行m列的整数矩阵，再输入q个询问，每个询问包含四个整数x1,y1,x2,y2，表示一个子矩阵的左上角坐标和右下角坐标。

对于每个询问输出子矩阵中所有数的和。

输入格式

第一行包含三个整数n， m,q。

接下来n行，每行包含m个整数，表示整数矩阵。

接下来q行，每行包含四个整数x1,y1,x2,y2，表示一组询问。

输出格式

共q行，每行输出一个询问的结果。

数据范围

1 ≤n, m ≤ 1000,
1 ≤ q ≤ 100000,
1 ≤ x1 ≤ x2 ≤ n,
1 ≤ y1 ≤ y2 ≤ m,
—1000 ≤ 矩阵内元素的值 ≤ 1000

输入样例

3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4

输出样例

17
27
21

import java.util.Scanner;

public class SubMatrix{

    static Scanner scanner = new Scanner(System.in);
    static final int N = 1010;
    static int n = scanner.nextInt();
    static int m = scanner.nextInt();
    static int q = scanner.nextInt();
    static int[][] a = new int[N][N];
    static int[][] s = new int[N][N];

    public static void main(String args[]) throws Exception {
        for(int i = 1; i <= n; i++)
            for(int j = 1; j <= m; j++)
                a[i][j] = scanner.nextInt();

        for(int i = 1; i <= n; i++)
            for(int j = 1; j <= m; j++)
                s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + a[i][j]; // 求前缀和


        while(q-- > 0)
        {
            int x1=scanner.nextInt();
            int y1=scanner.nextInt();
            int x2=scanner.nextInt();
            int y2=scanner.nextInt();
            System.out.println(s[x2][y2] - s[x1-1][y2] - s[x2][y1-1] + s[x1-1][y1-1]); // 计算子矩阵的和
        }
    }

}