拓扑排序

1、拓扑排序

有向图的拓扑序列就是图的宽度优先遍历的应用

拓扑序列是针对有向图来说的，无向图是没有拓扑序列的。

存在一个序列A，对于图中的每条边（x，y），x在A中都出现在y之前，则称A是该图的一个拓扑序列。

举例：有如下一个有向图:

A = （1，2，3）就是一个拓扑序列，原因如下：

首先看第一条边（1，2）：1在2前面

在看第二条边（2，3）：2在3前面

最后看第三条边：（1，3）：1在3前面

图中每条边出现在序列A中时都是起点在终点的前面，所以A就是一个拓扑序列。

换句话说，我们把一个图按照拓扑序排好序之后，他所有的边都是从前指向后的。

并不是所有图都有拓扑序，如上图，我们把（1，3）改为（3，1），那么这个图就没有是没有拓扑序的。只要存在一个环我们就无论如何都不把他摆成拓扑序的形式。

有向无环图（又名：拓扑图）一定存在拓扑序列。

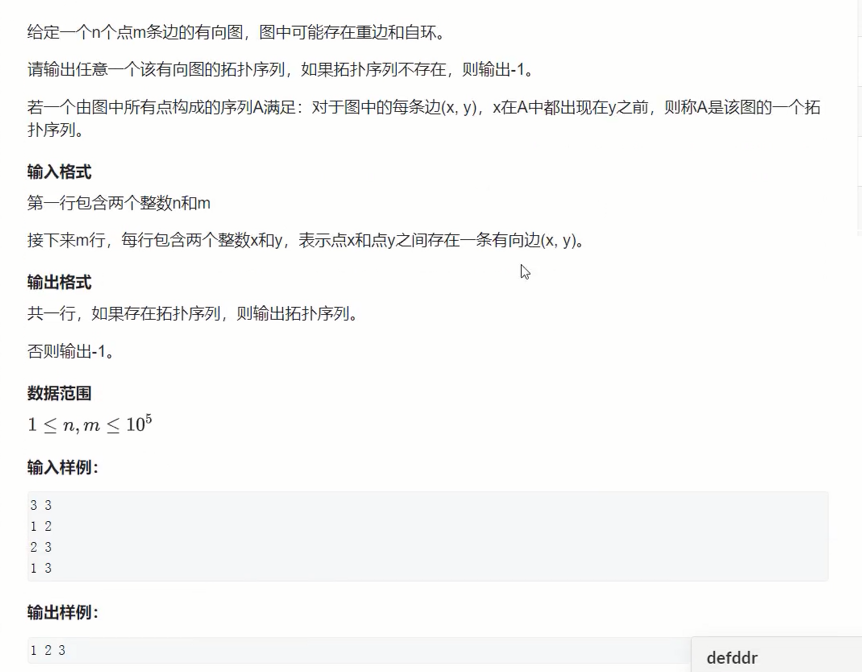
1.1 拓扑例题：有向图的拓扑序列

1.2 拓扑序列代码

拓扑序是从前指向后的，所以所有入度为0的点都可以作为起点。

• queue \(\gets\) 所有入度为0的点

• while（queue不空）

  {

  ​ \(t \gets\)队头

  ​ 枚举t的所有出边：\(t \to j\)

  ​ 删掉\(t \to j\)，这影响了j的入度，用d[j]表示j的入度，所以d[j]--;

  ​ if(d[j] == 0)说明这前面所有的都排好序放好了，此时j就没有限制可以放到最前面了

  ​ \(queue \gets j\)，就让j入队

  }

拓扑序不唯一。

/**
 * 所有当前入度为0的点都可以作为起点
 * 这意味着没有边指向它，即没有点在它前面
 * d[j]表示j的入度
 * queue <-- 所有入度为0的点
 * while queue 不空
 * {
 *      t <-- 对头
 *      枚举t的所有出边 t->j
 *      删掉t->j，d[j]--;
 *      if d[j] == 0 说明j前面所有点都排好序了，都放好了，没有限制了
 *      queue <- j;
 * }
 */
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010;

int n, m;
int h[N], e[N], ne[N], idx;
int d[N];
int q[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

bool topsort()
{
    int hh = 0, tt = -1; // 队头，队尾

    for (int i = 1; i <= n; i ++ )
        if (!d[i]) // 所有入度为0的点插入到队列内
            q[ ++ tt] = i;

    while (hh <= tt)
    {
        int t = q[hh ++ ];

        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i]; // 找到出边，然后入度--
            if (-- d[j] == 0) // =0说明找到了
                q[ ++ tt] = j;
        }
    }

    return tt == n - 1; // 是不是所有点都入队了，都进队说明是有向无环图
}

int main()
{
    scanf("%d%d", &n, &m);

    memset(h, -1, sizeof h);

    for (int i = 0; i < m; i ++ )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b); // 一条a->b的边，b的入度++

        d[b] ++ ;
    }

    if (!topsort()) puts("-1");
    else
    {
        for (int i = 0; i < n; i ++ ) printf("%d ", q[i]);
        puts("");
    }

    return 0;
}