堆

3.1 概述

手写堆而不是STL的堆

STL里的堆就是优先队列priority_queue

如何手写一个堆？

STL支持的操作：

1. 插入一个值
2. 求集合中的最小值
3. 删除最小值

STL没办法直接实现，只能间接实现的功能：

4. 删除任意一个元素
5. 修改任意一个元素

3.1.1 什么是堆

堆就是一个二叉树或者说是完全二叉树

完全二叉树：除了最后一层，其余层都是满节点。最后一层从左到右依次排列。

以小根堆为例：每一个点都是 \(\leq\) 左右儿子的叫小根堆

根节点就是树节点的最小值。

3.1.2 堆的存储

用一个一维数组来存，1号点是跟节点，x的左儿子是2x，右儿子是2x+1。

所以数组下标从1开始比较方便

3.1.3 堆的操作

• down(x)
• up(x)

比如有如下小根堆，根节点突然变为6

移动的逻辑关系：先从6，3，4这三个点中找到一个最小值3，把6和3进行交换，接下来在6，3，5中找到最小值3进行交换，一直交换到不能交换的情况，又恢复成了一个小根堆。如下所示：

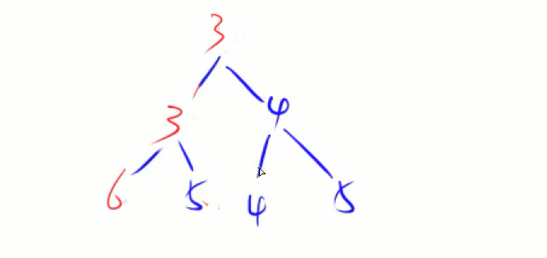
用up和down实现堆的五种操作

1、 插入实现

用heap表示这个堆，size表示堆的大小

插入x：heap[++size] = x，在堆的最后一个位置插入x

不断上移：up(size);

heap[++size] = x;
up(size);

2、求最小值

heap[1];

3、 删除最小值

我们想删除最小值，有一些技巧

1. 我们用整个堆的最后一个元素覆盖堆顶元素，之后size--删除最后一个元素就可以了。
2. 接下来不断下移down(size)就可以了。

原因：这个堆的实现是一个一维数组，我们删除头节点比较困难，但是删除尾节点非常方便。

heap[1] = heap[size];
size--;
down(1);

4、删除任意一个元素k

与删除最小值类似

heap[k] = heap[size];
size--;
// 此时k这个位置可能变大/变小/不变，三种情况，偷懒直接up，down，实际指挥执行一个
down(k);
up(k);

5、修改任意一个元素

heap[k] = x;
// 此时k这个位置可能变大/变小/不变，三种情况，偷懒直接up，down，实际指挥执行一个
down(k);
up(k);

3.2 练手题目

堆排序就是把整个数列或者数组建成堆，每一次把堆顶输出出来，第一次就是最小/大数，

第二次就是第二小/大的数，以此类推...

3.3 练手答案

#include<iostream>
#include<algorithm>
using namespace std;

const int N = 100010;

int n,m;
int h[N],size;

void down(int u)
{
    // log的复杂度，跟树的高度成正比
    int t = u;
    if(u*2 <= size && h[u*2] < h[t]) t = u*2;
    if(u*2+1 <= size && h[u*2+1] < h[t]) t = u*2+1;
    if(u != t)
    {
        swap(h[u],h[t]);
        down(t);
    }

}

void up(int u)
{
    while(u/2 && h[u/2] > h[u])
    {
        swap(h[u/2],h[u]);
        u /= 2;
    }
}

int main()
{
    cin >> n >> m;;
    for(int i = 1; i <= n; i++) cin >> h[i];
    size = n;

    // 一个一个插入复杂度为O(n*log^n),下面是一个O(n)的建堆方式
    // 因为每一次操作log^n,一共n步，所以下面的方法优化了时间复杂度
    // 这是一个递推问题
    for(int i = n/2; i; i--) down(i);
    while(m--)
    {
        cout << h[1] << " ";
        h[1] = h[size--];
        down(1);
    }
    return 0;

}

3.4 证明3.3中建堆的时间复杂度是O(n)

从n/2开始down，n/2正好是除了最后一层的所有元素

上面一半元素（第1，2，3层）的数量是n/2，最后一层（即第三层）元素数量是n/4，向下down1层，第二层的元素数量是n/8，向下down2层，第一层的数量是n/16，向下down3层

所以O = \(\frac{n}{4}\times 1 + \frac{n}{8} \times 2 + \frac{n}{16} \times 3 + ...\)

进行计算，得

\(n(\frac{1}{2^2} + \frac{2}{2^3} + \frac{3}{2^4} + \frac{4}{2^5} + ...)\)

令S = \((\frac{1}{2^2} + \frac{2}{2^3} + \frac{3}{2^4} + \frac{4}{2^5} + ...)\)

则2S = \((\frac{1}{2} + \frac{2}{2^2} + \frac{3}{2^3} + \frac{4}{2^4} + ...)\)

令2S - S = S,得\((\frac{1}{2} + \frac{1}{2^2} + \frac{1}{2^3} + \frac{1}{2^4} + ...)\)，这个结果是小于1的

所以整个的时间复杂度就是小于n的

所以时间复杂度为O(n)。