并查集

1、概述

1.1 作用

1. 将两个集合合并
2. 询问两个元素是否在一个集合当中

1.2 暴力做法

用一个数组belong[x] = a存储哪个元素属于哪个集合，判断就是if(belong[x] == belong[y])，复杂度O（1）

但是当我们想合并两个集合时，假如集合a有1000个元素，集合b有2000个元素，那么我们最少也需要改动集合a的1000个元素编号，很耗时

并查集优化：可以在近乎O(1)的时间完成上述两个操作

1.3 基本原理

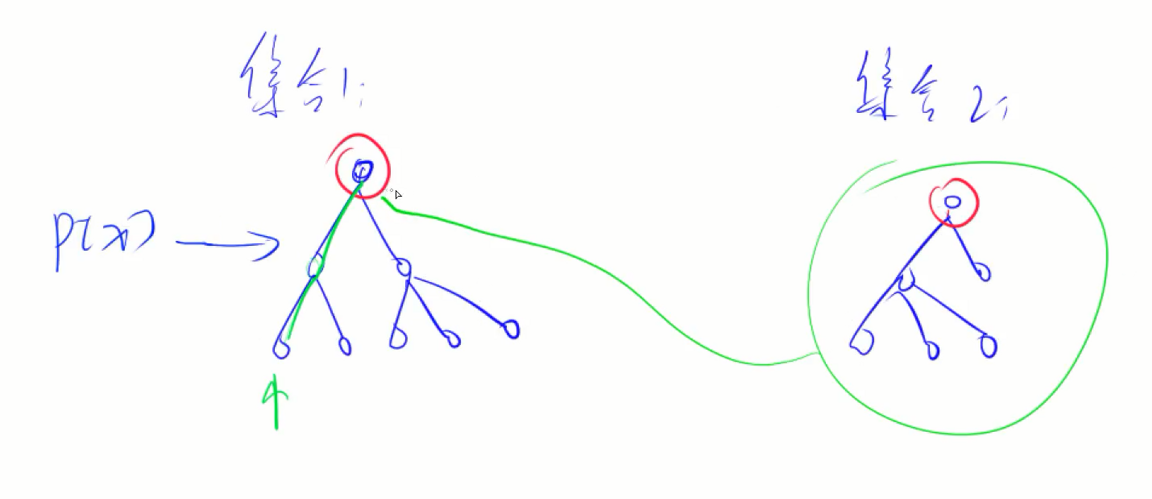
每一个集合用树的形式来维护。每一个集合的编号就是他根节点的编号。对于每个点都存储他的父节点是谁。p[x]表示x的父节点。当我们求每个点属于哪个集合的时候，就去查找他的父节点，看他的父节点是不是树根root节点，不是就继续向上找。

问题一：如何判断树根？

if(p[x] == x)，除了根节点外p[x]都 != x

问题二：如何求x的集合编号？

while(p[x] != x) x = p[x];

问题三：如何合并两个集合？

加一条边，把右面的集合变成左面集合的儿子。假设p[x]是x的集合编号，p[y]是y的集合编号，则让p[y] = x就可以了。

现在这种情况下，求x的集合编号复杂度还是蛮高的，每次都需要从当前的节点遍历到根节点，遍历的次数和树的高度是成正比的。这时就涉及到并查集的一个优化。

并查集优化：路径压缩

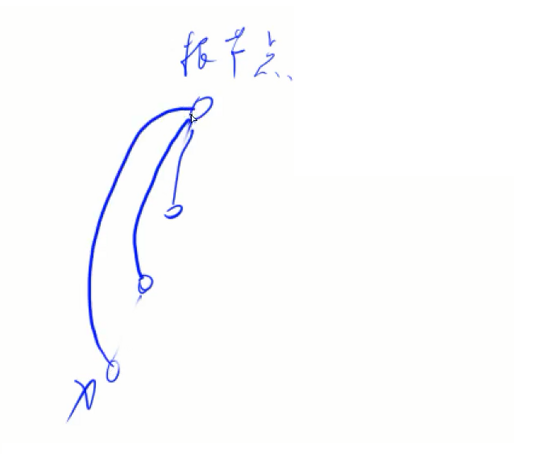
一旦往上走找到了根节点，就把这个路径上所有的点都直接指向根节点。这样的话如上图第一次需要走3步，下一次就只需要走一步了。

还有一种按秩合并的优化，但是用的比较少。

2、练手题目

3、练手答案

p[x]存储的是每个节点的父节点是谁，这道题里，初始时每个元素单独一个集合，每个集合内只有一个点，这个点树根就是自己p[x]=x就可以了。

#include<istream>
using namespace std;

const int N = 100010;

int n,m;
int p[N];

int find(int x) // 返回x的祖宗节点 + 路径压缩
{
    // 递归回溯时起到了路径压缩的作用，将每个点都指向了祖宗节点
    if(p[x] != x) p[x] =find(p[x]);
    return p[x];
}

int main()
{
    scanf("%d%d", &n,&m);
    for(int i = 1; i <= n; i++) p[i] = i;
    while(m--)
    {
        // scanf读取字符时不会读取空格和回车，但是读取字符串时会自动忽略空格和回车
        // 所以用的是op[2]而不是op
        // cin会自动忽略空格和回车，可以用op
        char op[2];
        int a,b;
        scanf("%s%d%d",op,&a,&b);
        if(op[0] == 'M') p[find(a)] = find(b); // 合并2个集合，a的祖宗节点的父亲=b的祖宗节点
        else
        {
            // 说明2节点在同一集合
            if(find(a) == find(b)) puts("Yes");
            else puts("No");
        }
    }
    return 0;
    
}