KMP

就是两个串，s[N]是长串，p[M]是短串

习惯上下标从1开始

暴力做法：

就相当于每次都只挪动一个位置去匹配下一位。红色和绿色圆圈说明这个位置不匹配，将红色短线向右移动一个位置重新匹配。

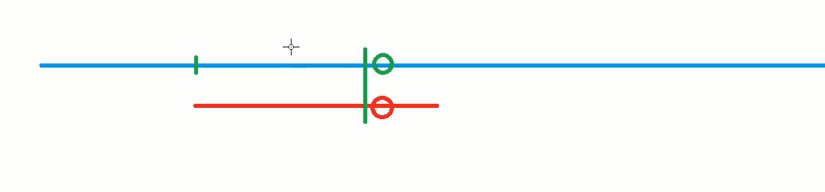
KMP优化：

从上面可以看出一些规律，在前面匹配失败的情况下，我们最多可以往后移动多少位让他继续匹配。

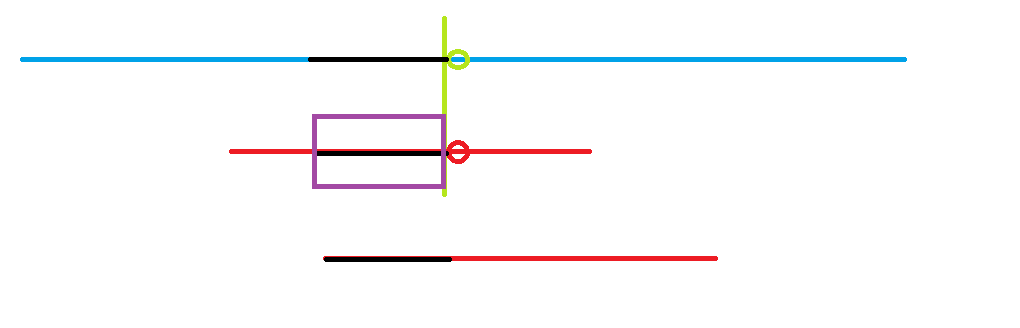
我们要找的实际上就是紫色框内这条黑色的线，这个黑线越长，也就是红色圈圈之前的线的部分的开头和结尾相同的值的数量越多，那么向后移动的位置也就越少。

那么实际上我们只需要对红色串的数组的每个点都预处理出后缀和前缀最大相等的长度是多少。这个就是所谓next数组的含义。next[i]就是以i为终点的后缀和从1开始的前缀相等且后缀长度最长。

举例说明next数组：

假设这个匹配串叫p，next[i] = j的含义就是说：

p[1~j] = p[i-j+1~i]，即这两段是相等的，即上图中两个红色部分相等且长度最长。

明确一下各个点的下标：

在上一个串匹配到i-1时，模板串匹配到j时，是相等的，但是s[i] != p[j+1],此时就需要把红颜色的线从前往后移动。

移动之后如图：

然后看紫色圆圈与s[i]即绿色圆圈是否匹配，如果匹配说明我们可以继续往后做，如果不匹配，我们就递归的做这个过程，再把红色线向后移动ne[ne[j]]的位置，之后看是否匹配。

1、练手题目

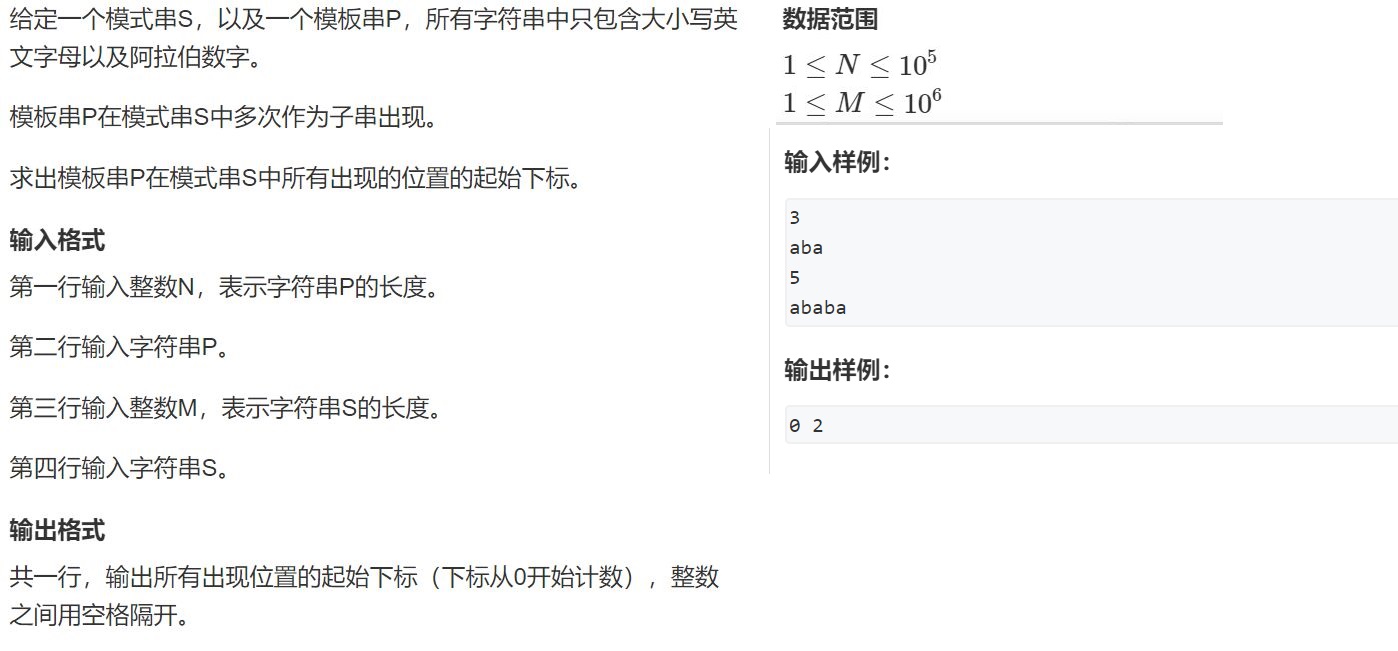
2、练手答案

// 注意：试图和s[i]匹配的是p[j+1]
#include<iostream>

using namespace std;

const int N = 10010,M = 100010;

int n,m;
int ne[N];
char s[M],p[N];

int main()
{
    cin >> n >> p+1 >> m >> s+1;

    // 求next的过程
    // next用的是模板串即字串p而不是模式串即总串s
    // 与i匹配的是j+1，所以j往前错了一位
    // n是字串p的总长度

    for(int i = 2, j = 0; i <= n; i++)
    {
        // 在不停匹配中寻找next数组
        while(j && p[i] != p[j+1]) j = ne[j];

        // 退出循环有两种情况，退无可退和匹配成功
        if(p[i] == p[j+1]) j++; // 匹配成功，j到下一步
        ne[i] = j; // 记录一下
    }

    // KMP匹配过程                                                                         
    for(int i = 1, j = 0; i <= m; i++)
    {
        // j没有退回起点，j退回起点表示重新开始匹配
        // 不匹配就移动一下，j=ne[j]
        // 每次不成功都可以退一步但是j退到开头退无可退就没办法了
        // 假设第i个点和第j+1个点不匹配
        // 不满足这些条件则进行移动最大前缀和后缀相等的距离
        // j没退回起点，退回起点含义就是需要重新开始匹配
        while(j && s[i] != p[j+1]) j = ne[j];// j不能往后走就往前退一步

         // 结束有两种情况，退无可退或成功匹配
        if(s[i] == p[j+1]) j++;// 如果匹配，则j到下一个位置
        if(j == n)
        {
            // 匹配成功
            printf("%d %d",i-n, i-1);
            cout << endl;
            j = ne[j]; // 匹配成功后如果想继续匹配就移动ne[j]的距离，此题用不到
        }
    }
    return 0;
}

3、求next数组

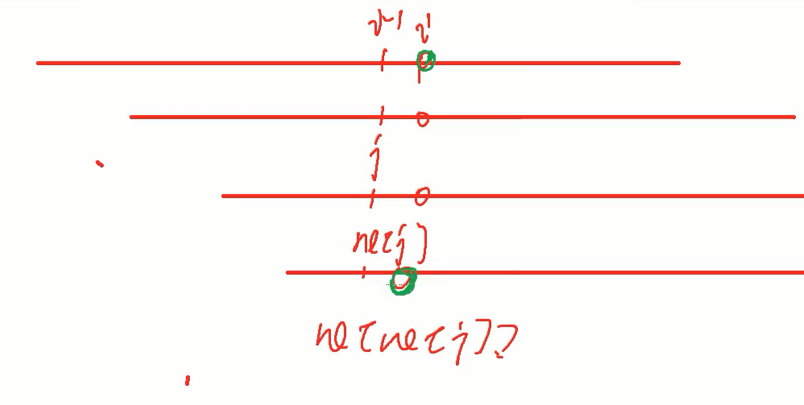
就是这样不断循环往复，不断找到合适的位置

i从2开始，因为next[1]=0，因为第一个字母失败了就只能从0开始

for(int i = 2, j = 0; i <= n; i++)
    {
        // 在不停匹配中寻找next数组
        while(j && p[i] != p[j+1]) j = ne[j];

        // 退出循环有两种情况，退无可退和匹配成功
        if(p[i] == p[j+1]) j++; // 匹配成功，j到下一步
        ne[i] = j; // 记录一下
    }

具体图示如下：

s[7] != p[7],j = 6，ne[6] = 4,所以j = 4，不匹配在继续往前跳，直到跳到开头为止。

4、时间复杂度

这里给出的代码的复杂度是O(N)的。

while循环最多执行m次，所以j最多会加m次，i循环m次，j最多减m次，所以虽然是2重循环，但实际的复杂度为2m