归并排序

归并排序 O(\(n\log_an\))

主要思想

分治

快排是用一个数来分，让左边都小于等于这个数，右面都大于等于这个数。

归并是以整个数组最中心来分。

具体步骤

1. 确定分界点mid即下标长度中间值，取左右平均值\(\frac{(l+r)}{2}\)即可

2. 递归排序左边left和右边right

3. 归并：把两个有序的数组合并在一起 O(n)

具体代码实现

双指针算法

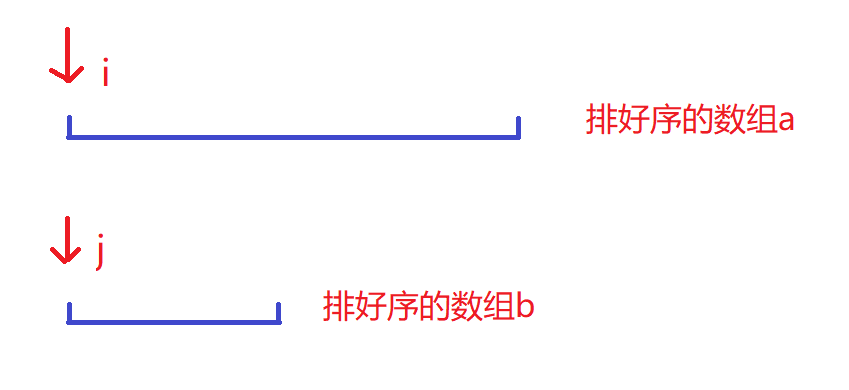
如图所示，i和j指针指向的数进行对比，小的数放入结果数组c中，对应的指针向后移动一位

直至i和j一方走到头，将剩余数组全部放入结果数组c中，如i走到末尾，那么就将j++将其对应的数也放到结果数组C中

归并排序是稳定的，快速排序是不稳定的，这个稳定和不稳定是什么意思呢？

比如有两个排好序的数组

1. 1 3 5 7 9

2. 2 4 5 8 10

对于归并排序来说当i，j指针都指向5时，每次都固定将i移动到下一位，所以是稳定的

但是对于快速排序来说，并不能确定每次移动哪个数组中对应5的指针。

快速排序想变成稳定的，只需要将排序的数变成pair就可以了，如5--><5,1>,<5,2>

稳定和不稳定是指对于相同的值来说每次放在前面的是不是都是固定的。

复杂度分析

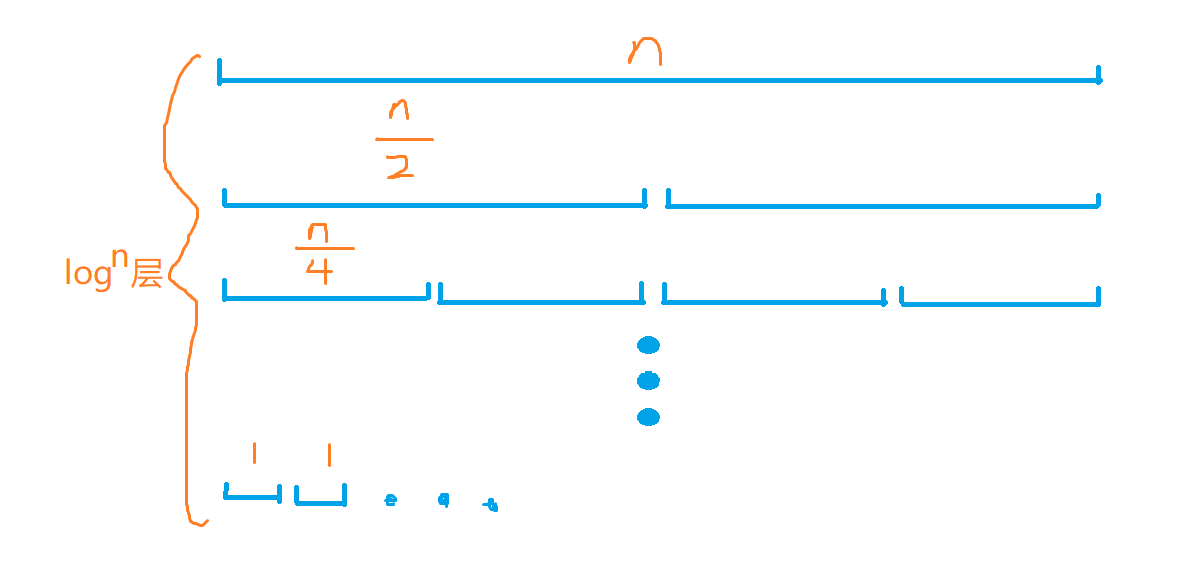
每一层的时间复杂度都是O(n)的。所以总的时间复杂度O(\(n\log_an\))

代码

#include<iostream>

using namespace std;

const int N = 100010;

int n;
int q[N],tmp[N];

void merge_sort(int q[], int l, int r)
{
    if(l >= r) return;
    int mid = l+r >> 1;
    merge_sort(q,l,mid);
    merge_sort(q,mid+1,r);
     // 归并
     // 表示当前tmp里有多少个数
     int k = 0,i = l, j = mid+1;
     while(i <= mid && j <= r)
        {
            if(q[i] <= q[j]) tmp[k ++] = q[i ++];
            else tmp[k ++] = q[j ++]; 
        }
        while(i <= mid) tmp[k ++] = q[i ++];
        while(j <= r) tmp[k ++] = q[j ++];
    
        for(int i = l, j = 0; i <= r; i++,j++) q[i] = tmp[j];
}


int main()
{
    scanf("%d",&n);
    for(int i = 0; i < n; i++) scanf("%d",&q[i]);
    merge_sort(q,0,n-1);
    for(int i = 0; i < n; i++) printf("%d ", q[i]);
    return 0;
}