二分

二分

在一个区间内部去二分答案，在选择二分出的两个区间的时候都选择答案所在区间进行下一步处理，

这样可以保证区间缩小了一半并且答案也在该区间内，当区间长度为1时，区间内的数就是答案

二分的本质：

1. 如果有单调性一定可以二分，但是可以二分的题目不一定有单调性。

2. 边界：即定义某种性质，将整个区间一分为二，使得左面可以满足这种性质，右边不满足这种性质

整数二分

整数二分有着边界的问题，如(4+5)/2

具体如下图所示：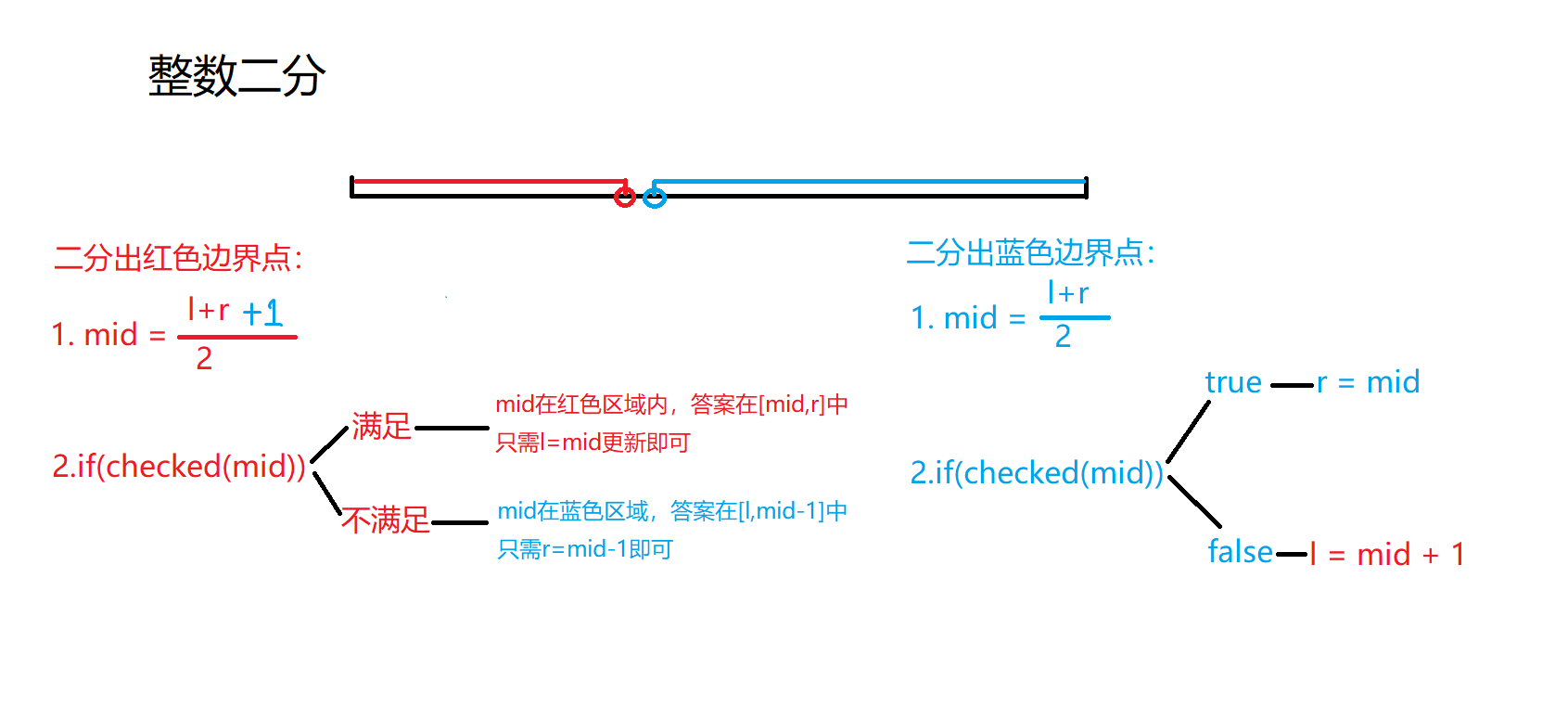

为什么在二分红色边界点时mid=\(\frac{l+r+1}{2}\)而不是\(\frac{l+r}{2}\)呢?

假设我们让mid=\(\frac{l+r}{2}\),那么当l=r-1时，在进行一次更新后，由于C++的除法性质，mid=r-1=l。

此时check如果为true，则l=mid=l，程序仍是[l,r],这时程序将进入无限循环，所以让mid=\(\frac{l+r+1}{2}\)。

总结一下，如果更新是l=mid,那么mid=\(\frac{l+r+1}{2}\)。如果更新是r=mid,那么mid=\(\frac{l+r}{2}\)。

代码实现

实际在代码实现过程中并没有上面那么复杂，首先上模板

bool check(int x) {/* ... */} // 检查x是否满足某种性质

// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check()判断mid是否满足性质
        else l = mid + 1;
    }
    return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

然后上一道题目

题目名称：寻找数的范围

给定一个按照升序排列的长度为n的整数数组，以及 q 个查询。

对于每个查询，返回一个元素k的起始位置和终止位置（位置从0开始计数）。

如果数组中不存在该元素，则返回“-1 -1”。

输入格式

第一行包含整数n和q，表示数组长度和询问个数。

第二行包含n个整数（均在1~10000范围内），表示完整数组。

接下来q行，每行包含一个整数k，表示一个询问元素。

输出格式

共q行，每行包含两个整数，表示所求元素的起始位置和终止位置。

如果数组中不存在该元素，则返回“-1 -1”。

数据范围

1≤n≤100000
1≤q≤10000
1≤k≤10000

输入样例

6 3
1 2 2 3 3 4
3
4
5

输出样例

3 4
5 5
-1 -1

代码实现

#include <iostream>

using namespace std;

const int N = 100010;

int n, m;
int q[N];

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 0; i < n; i ++ ) scanf("%d", &q[i]);

    while (m -- )
    {
        int x;
        scanf("%d", &x);

        int l = 0, r = n - 1;
        while (l < r)
        {
            int mid = l + r >> 1;

            // 找到第一个边界
            // 性质定为>=x,说明mid一定在右半边，答案一定在左半边
            if (q[mid] >= x) r = mid;
            else l = mid + 1;
        }

        // 不存在x的情况
        if (q[l] != x) cout << "-1 -1" << endl;
        else
        {
            // while循环结束l，r相等，输出l/r都可以
            cout << l << ' ';

            // 性质定位<=x
            // 找第二个边界，此时左边所有数都满足这个性质
            // 右边所有数都不满足这个性质
            int l = 0, r = n - 1;
            while (l < r)
            {
                int mid = l + r + 1 >> 1;
                if (q[mid] <= x) l = mid; // 说明mid在左半边，答案在mid右半边
                else r = mid - 1;
            }

            cout << l << endl;
        }
    }

    return 0;
}

浮点数二分