POJ1458最长公共子序列

原题链接:Common Subsequence

题目描述

给出两个字符串，求出这样一个最长的公共子序列的长度：子序列中的每个字符都能在两个原串中找到，而且每个字符的先后顺序和原串中的先后顺序一致。

样例输入

abcfbc         abfcab
programming    contest 
abcd           mnp

样例输出

4
2
0

---

动态规划 \(O(n^2)\)

这道题首先需要对集合进行划分，我们要找的是最长的公共子序列，这个需要找的集合就是所有在字符串a中的前i个字母中出现，且在字符串b的前j个子母中出现的集合。
我们需要对整个集合进行划分，如下图所示：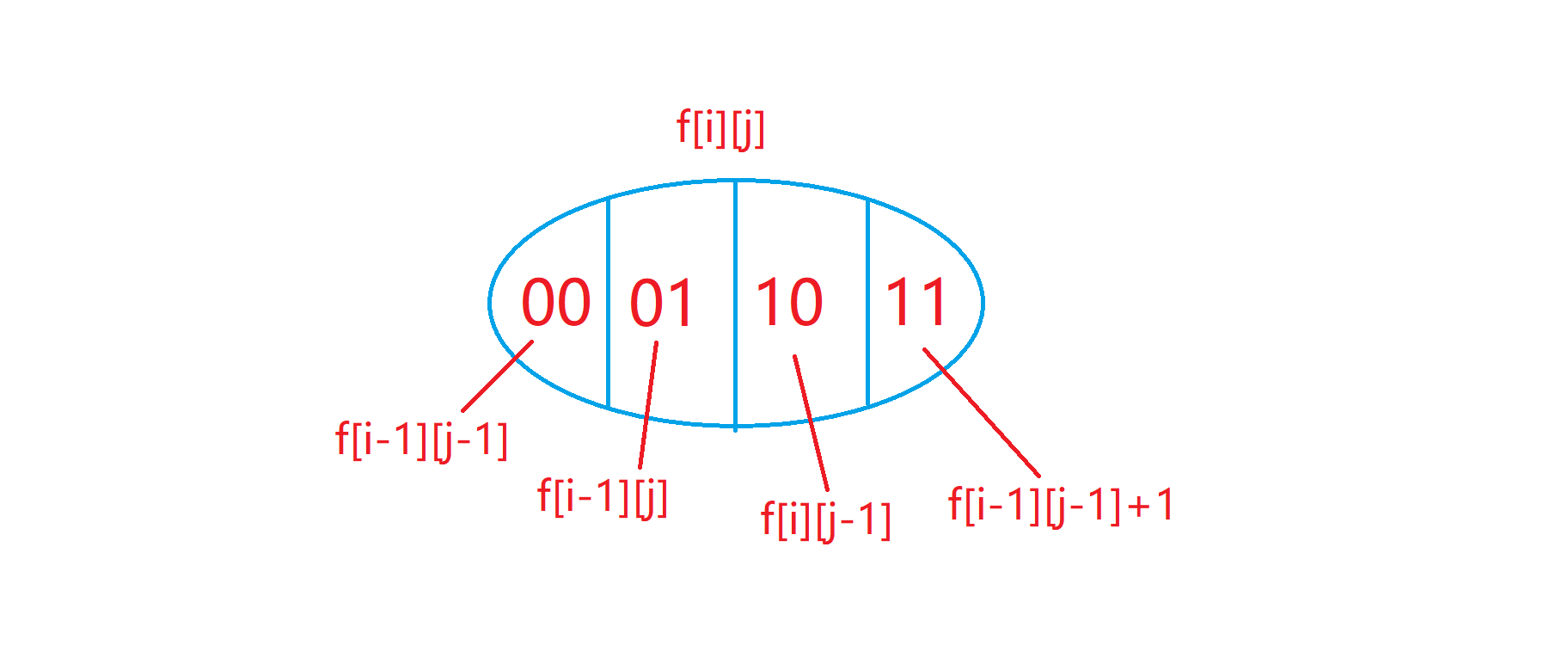
整个集合是按照a[i]和b[j]是否包含在子序列中进行的划分，00表示都不在，01表示a[i]不在b[j]在，10表示a[i]在b[j]不在，11表示a[i],b[j]都在，其中00很容易得其表示方法f[i-1][j-1],11也很容易得其表示方法，f[i-1][j-1]+1,01和10这两种情况中，f[i-1][j]表示的并不一定就包含b[j],f[i-1][j]代表的实际是b[j]这个值在b序列的前j个字母中出现过，但并不一定就是最后一个位置即位置j，但是f[i-1][j]有没有可能包换01这种情况呢，可能的，因为f[i-1][j]是一个更大的集合，01只是这个集合的一个特殊情况，而f[i-1][j]又一定包含在f[i][j]中，所以我们用f[i-1][j]对01进行表示，10同理。
这四个集合的划分彼此之间是有交集的，比如f[i-1][j-1]就一定包含在f[i-1][j]/f[i][j-1]中，所以f[i-1][j-1]这个集合的划分在代码中就被省略了。

时间复杂度

动态规划的问题的时间复杂度计算方法：
状态数量是\(O(n^)2\),因为是2维的，即集合的状态划分
状态转移是3次运算，O(1)的
总体时间复杂度就是\(O(n^2 * 1)\)

C++ 代码

#include<iostream>
#include<string>

using namespace std;

const int N = 1010;

string a, b;
int f[N][N];

int main()
{
    while(cin >> a >> b)
    {
        for(int i = 1; i <= a.length(); i++)
            for(int j = 1; j <= b.length(); j++)
            {
                f[i][j] = max(f[i-1][j], f[i][j-1]);
                if(a[i-1] == b[j-1]) f[i][j] = max(f[i][j], f[i-1][j-1]+1);
            }

        cout << f[a.length()][b.length()] << endl;
    }
    return 0;
}