[Intro to Deep Learning with PyTorch -- L2 -- N35] Code: Analyzing Student Data
Predicting Student Admissions with Neural Networks
In this notebook, we predict student admissions to graduate school at UCLA based on three pieces of data:
- GRE Scores (Test)
- GPA Scores (Grades)
- Class rank (1-4)
The dataset originally came from here: http://www.ats.ucla.edu/
Loading the data
To load the data and format it nicely, we will use two very useful packages called Pandas and Numpy. You can read on the documentation here:
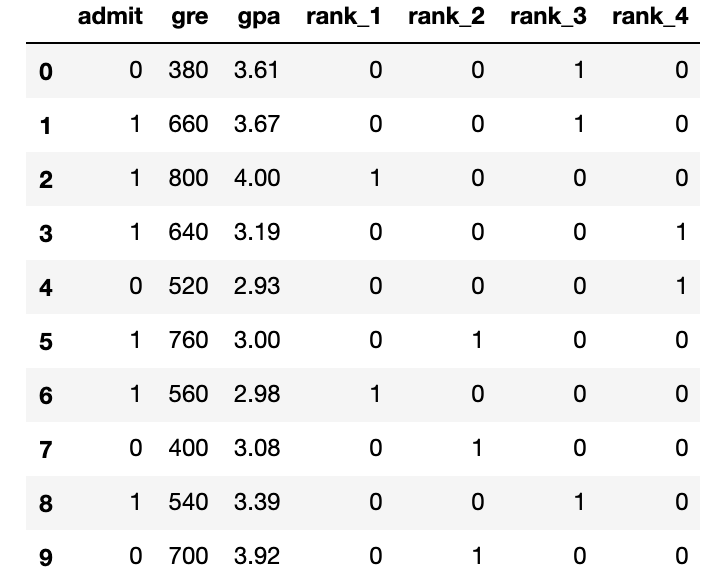
# Importing pandas and numpy import pandas as pd import numpy as np # Reading the csv file into a pandas DataFrame data = pd.read_csv('student_data.csv') # Printing out the first 10 rows of our data data[:10]
Plotting the data¶
First let's make a plot of our data to see how it looks. In order to have a 2D plot, let's ingore the rank.
# Importing matplotlib import matplotlib.pyplot as plt # Function to help us plot def plot_points(data): X = np.array(data[["gre","gpa"]]) y = np.array(data["admit"]) admitted = X[np.argwhere(y==1)] rejected = X[np.argwhere(y==0)] plt.scatter([s[0][0] for s in rejected], [s[0][1] for s in rejected], s = 25, color = 'red', edgecolor = 'k') plt.scatter([s[0][0] for s in admitted], [s[0][1] for s in admitted], s = 25, color = 'cyan', edgecolor = 'k') plt.xlabel('Test (GRE)') plt.ylabel('Grades (GPA)') # Plotting the points plot_points(data) plt.show()
Roughly, it looks like the students with high scores in the grades and test passed, while the ones with low scores didn't, but the data is not as nicely separable as we hoped it would. Maybe it would help to take the rank into account? Let's make 4 plots, each one for each rank.
# Separating the ranks data_rank1 = data[data["rank"]==1] data_rank2 = data[data["rank"]==2] data_rank3 = data[data["rank"]==3] data_rank4 = data[data["rank"]==4] # Plotting the graphs plot_points(data_rank1) plt.title("Rank 1") plt.show() plot_points(data_rank2) plt.title("Rank 2") plt.show() plot_points(data_rank3) plt.title("Rank 3") plt.show() plot_points(data_rank4) plt.title("Rank 4") plt.show()
# TODO: Make dummy variables for rank one_hot_data = pd.concat([data, pd.get_dummies(data['rank'], prefix='rank')], axis=1) # TODO: Drop the previous rank column one_hot_data = one_hot_data.drop('rank', axis=1) # Print the first 10 rows of our data one_hot_data[:10]
Scaling the data
The next step is to scale the data. We notice that the range for grades is 1.0-4.0, whereas the range for test scores is roughly 200-800, which is much larger. This means our data is skewed, and that makes it hard for a neural network to handle. Let's fit our two features into a range of 0-1, by dividing the grades by 4.0, and the test score by 800.
# Making a copy of our data processed_data = one_hot_data[:] # TODO: Scale the columns processed_data['gre'] = processed_data['gre'] / 800 processed_data['gpa'] = processed_data['gpa'] / 4.0 # Printing the first 10 rows of our procesed data processed_data[:10]
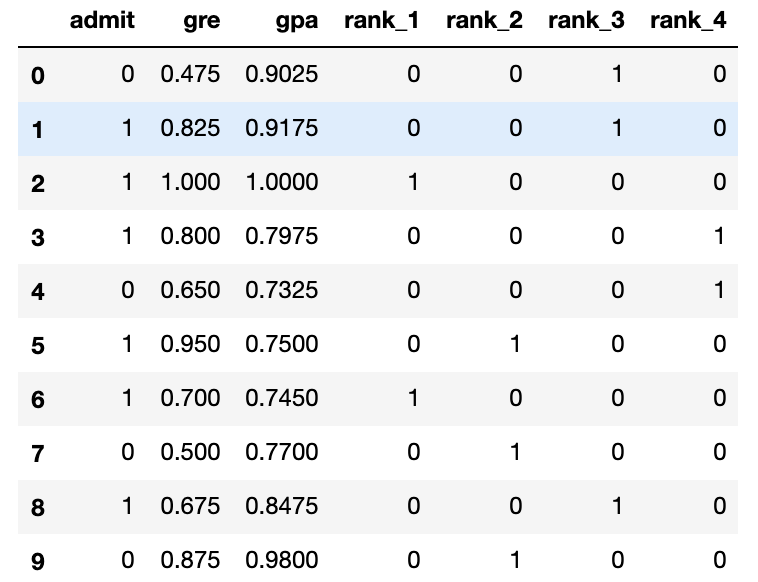
Splitting the data into Training and Testing
In order to test our algorithm, we'll split the data into a Training and a Testing set. The size of the testing set will be 10% of the total data.
sample = np.random.choice(processed_data.index, size=int(len(processed_data)*0.9), replace=False) train_data, test_data = processed_data.iloc[sample], processed_data.drop(sample) print("Number of training samples is", len(train_data)) print("Number of testing samples is", len(test_data)) print(train_data[:10]) print(test_data[:10])
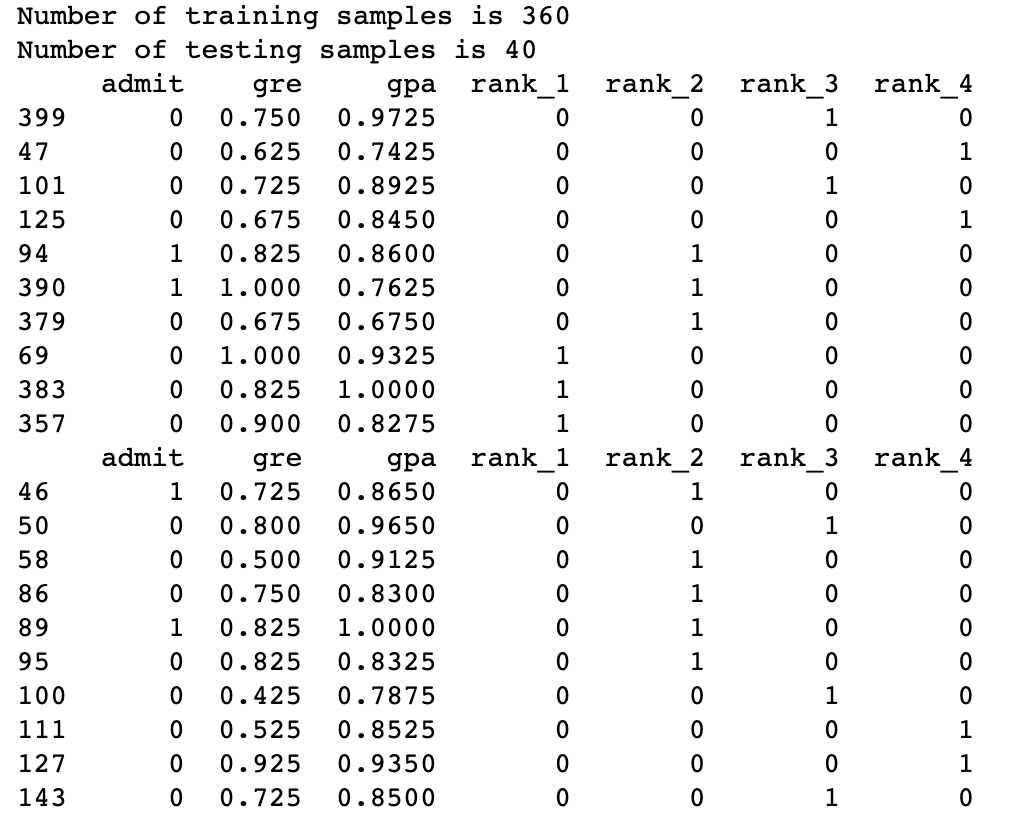
Splitting the data into features and targets (labels)
Now, as a final step before the training, we'll split the data into features (X) and targets (y).
features = train_data.drop('admit', axis=1) targets = train_data['admit'] features_test = test_data.drop('admit', axis=1) targets_test = test_data['admit'] print(features[:10]) print(targets[:10])
Training the 2-layer Neural Network
The following function trains the 2-layer neural network. First, we'll write some helper functions.
# Activation (sigmoid) function def sigmoid(x): return 1 / (1 + np.exp(-x)) def sigmoid_prime(x): return sigmoid(x) * (1-sigmoid(x)) def error_formula(y, output): return - y*np.log(output) - (1 - y) * np.log(1-output)Backpropagate the errorNow it's your turn to shine. Write the error term. Remember that this is given by the equation $$ (y-\hat{y}) \sigma'(x) $$
Backpropagate the error
Now it's your turn to shine. Write the error term. Remember that this is given by the equation
(𝑦−𝑦̂ )𝜎′(𝑥)
def error_term_formula(x, y, output): return (y-output) * sigmoid_prime(x)
# Neural Network hyperparameters epochs = 1000 learnrate = 0.5 # Training function def train_nn(features, targets, epochs, learnrate): # Use to same seed to make debugging easier np.random.seed(42) n_records, n_features = features.shape last_loss = None # Initialize weights weights = np.random.normal(scale=1 / n_features**.5, size=n_features) for e in range(epochs): del_w = np.zeros(weights.shape) for x, y in zip(features.values, targets): # Loop through all records, x is the input, y is the target # Activation of the output unit # Notice we multiply the inputs and the weights here # rather than storing h as a separate variable output = sigmoid(np.dot(x, weights)) # The error, the target minus the network output error = error_formula(y, output) # The error term error_term = error_term_formula(x, y, output) # The gradient descent step, the error times the gradient times the inputs del_w += error_term * x # Update the weights here. The learning rate times the # change in weights, divided by the number of records to average weights += learnrate * del_w / n_records # Printing out the mean square error on the training set if e % (epochs / 10) == 0: out = sigmoid(np.dot(features, weights)) loss = np.mean((out - targets) ** 2) print("Epoch:", e) if last_loss and last_loss < loss: print("Train loss: ", loss, " WARNING - Loss Increasing") else: print("Train loss: ", loss) last_loss = loss print("=========") print("Finished training!") return weights weights = train_nn(features, targets, epochs, learnrate)
Epoch: 0 Train loss: 0.272834785819 ========= Epoch: 100 Train loss: 0.214783568962 ========= Epoch: 200 Train loss: 0.212824240445 ========= Epoch: 300 Train loss: 0.211832049153 ========= Epoch: 400 Train loss: 0.211288707425 ========= Epoch: 500 Train loss: 0.210955131451 ========= Epoch: 600 Train loss: 0.210722118768 ========= Epoch: 700 Train loss: 0.21053904423 ========= Epoch: 800 Train loss: 0.210381907513 ========= Epoch: 900 Train loss: 0.210239075095 ========= Finished training!
# Calculate accuracy on test data test_out = sigmoid(np.dot(features_test, weights)) predictions = test_out > 0.5 accuracy = np.mean(predictions == targets_test) print("Prediction accuracy: {:.3f}".format(accuracy))
Prediction accuracy: 0.825
浙公网安备 33010602011771号