BUAA OO Summary - Unit1

Unit1

目录

目录

• Unit1
  • 目录
  • Task1架构
    • 读入处理
    • package parser---解析表达式（用递归下降法构造表达式树状结构）
      • Lexer
      • Parser
        • 关于对符号的处理
    • package expression---表达式存储架构
    • 化简表达式
      • 关于优化
    • 生成数据
  • Task2架构
    • 文件树
    • 关于重构
      • 架构
      • 化简
      • 合并
    • 迭代开发
  • Task3架构
  • 基于度量分析
    • TASK1
      • 代码规模分析
      • 方法复杂度分析
      • 类复杂度分析
    • TASK2与TASK3
      • 代码规模分析
      • 方法复杂度分析
      • 类复杂度分析
  • 分析自己程序的bug
    • TASK1
    • TASK2
    • TASK3
  • 分析别人程序的bug
    • TASK1
    • TASK2
    • TASK3
  • 架构设计体验

Task1架构

所谓万事开头难，当看到第一次作业以后，觉得很没有头绪：不知道怎么解析字符串，不知道是应该一遍解析表达式一遍进行化简还是解析完了以后再化简...总之就是，顶层架构无法确认，具体细节也不知道怎么实现。于是在反复阅读指导书并且与朋友进行交流以后，才开始进入正式的写代码阶段。虽然后面终于有了一个可以实现的想法，但是心里隐隐觉得，下周一定是要重构了。

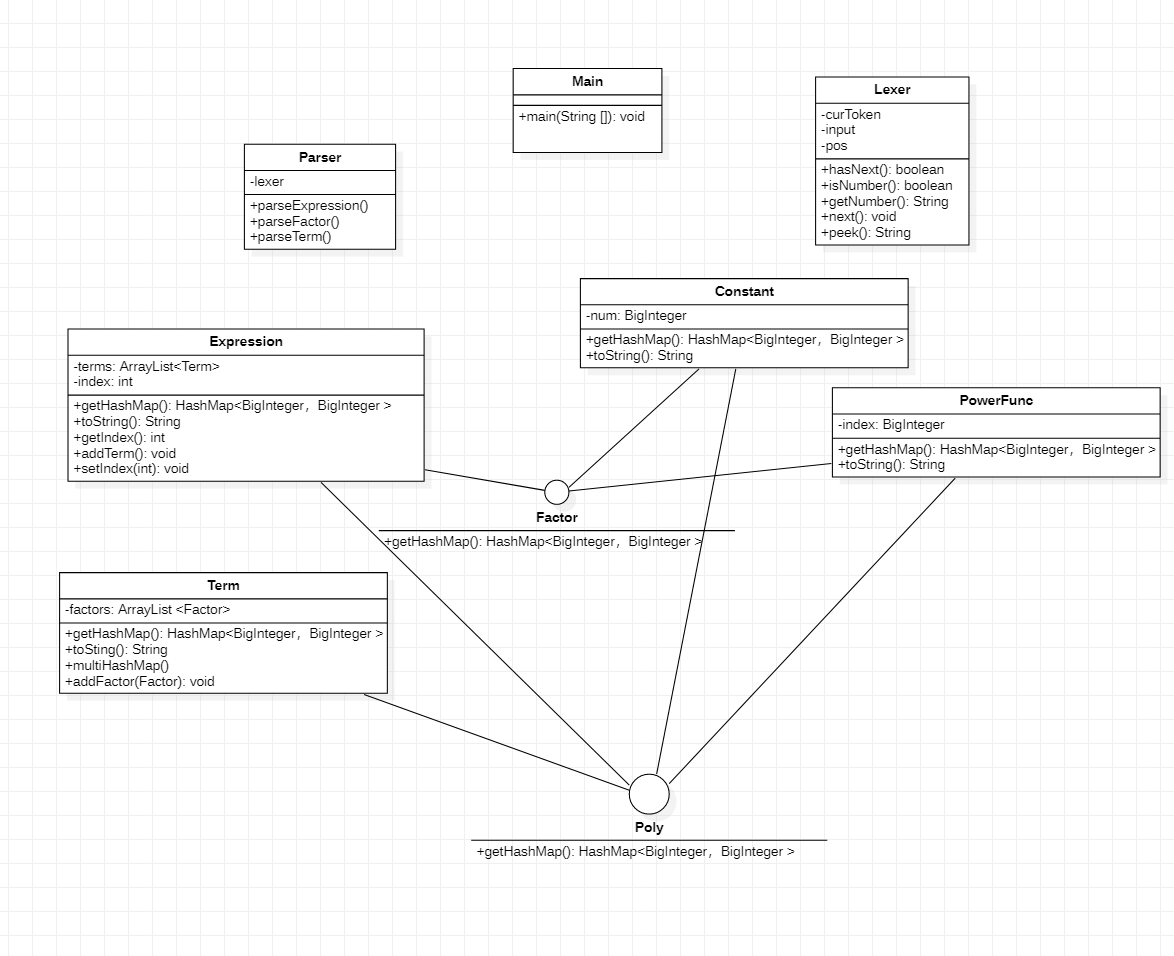
首先宏观来看整个解题步骤，分为一下几步

读入处理

首先，当读入字符串后，由于本次作业不进行错误格式判断，所以可以直接在这一步先把空白符全部去除，再进行下一步的表达式解析

package parser---解析表达式（用递归下降法构造表达式树状结构）

这里沿用模仿了训练代码中给出的Lexer类和Parser类

Lexer

Lexer用来扫描输入的字符串，并且匹配我们所需要的的token，其中的peek()方法可以让我们获取当前所读到的token，而每当我们读到某一个token并成功解析后，可以调用其中的next()方法，来继续解析下一个token，直到整个表达式解析完为止，也就完成了整个表达式树的构建

这里支持获取的token包含：['+'，'-'，'*'，'**'，'('，')'，不带符号的数字]

Parser

从形式化表述中可以清晰的知道，表达式由项通过加减号连接组成，而项由因子相乘组成，因子由变量因子、常数因子、表达式因子组成

所以这里很自然分为parseExpression,parseTerm,parseFactor来从顶层整个字符串逐个解析表达式

关于对符号的处理

这里，参照形式化表述，为了统一处理，降低复杂度

• 在parseExpression中对表达式的解析过程中，认为所有项都是由加号连接，而每一项前面的符号则归并至该项自身。这样也统一了第一项前面有符号的情况。

  当遇到负号，就在parseTerm以后返回的Term中再加入一个值为-1的常数因子（最后会进行合并同类型和化简处理），即相当于让解析到的当前项再乘上一个-1的因子；

  而当遇到正号，我们就可以不做处理，直接把解析完的项加入当前表达式就好

• 在parseTerm中对项进行解析时，参照形式化表述中，如果最前面的加减符号存在且为负号，则直接在这个项中加入一个值为-1的表达式因子，相当于整个项×-1

• 而在parseFactor中，需要特殊处理的表达式因子，判断如果扫描到'('，则parseExpression，即表达式因子；在解析完表达式因子后，如果遇到token'**'，则记录其后面的数值（注意这里要记得处理指数的符号），记录下来，然后在返回到parseTerm时，向该向中添加相应数值次的表达式因子

  比如：（x+1)**2，即向项中添加两次（x+1)，效果相当于（x+1）*（x+1）

package expression---表达式存储架构

这里设置了两个接口，主要是为了不混淆term

• Factor接口（显然因为下面三个都是因子）
  • PowerFunc
  • Constant
  • Expression
• Poly接口（里面有一个getHashMap方法，其实下面四个都能看成一个多项式存进HashMap中，下面化简表达式部分讲述，只不过后三个看成该多项式只含有一个项，HashMap中的key表示指数，value表示系数）
  • Term
  • PowerFunc
  • Constant
  • Expression

化简表达式

getHashMap()

从最底层因子类factors：幂函数、常数、表达式因子，得到他们对应的hashmap

比如对于幂函数x**2,其hashmap为<key: 2, value: 1>

对于常数1,其hashmap为<key: 0, value: 1>

对于表达式因子x**2+x+1,其hashmap为<key: 0, value: 1>,<key:1, value: 1>, <key: 2, value:1>

再在项类term，对这些因子的hashmap迭代相乘，逐渐拆括号，类似于当求（x+1)×(x+2)×(x+3),先得到（x^{2+3x+2)×(x+3)后，再拆一次括号为最终的（x}3+6x^2+11x+6)；最后得到的每个项都将是不含有表达式因子的项，即括号拆除完毕

得到term展开括号后的hashmap，最后在表达式类expression，把这些已经拆过括号的项再合并，达到最终的hashmap，即hashmap相加

最后在main里面得到返回的hashmap这是就已经是合并同类项以后的最简形式了

最终只需调用expression里面的toString方法，利用hashmap逐个打印出a*x**b形式的项的和即可

这里的gethashmap实则也是递归下降

关于优化

为了使得最后输出的结果在正确的前提下尽可能的短，最后在expression里面的toString方法要进行一下特判与处理；

比如当指数为0时，，即hashmap的key为0时，不打印指数部分；当指数为1，不打印“**1”；

生成数据

用到了python的Xeger，利用正则表达式来生成最基本的常数因子和表达式因子

然后写了几个函数分别用来生成

• 不含表达式因子的项
• 不含表达式因子的表达式（即用来生成表达式因子）
• 含表达式因子的项
• 表达式

Task2架构

果不其然，先预告一下，真的重构了。不过，重构不可怕，因为有了好的架构，才能有利于后期更好的迭代开发，这也让我在第三次作业尝到了很大的甜头。所以，一定要设计一个自己觉得至少不错的架构，如果自己都不能和自己的架构和解，问题早晚会暴露出来

文件树

│  InputHandle.java
│  Main.java
│
├─expression
│      Adder.java
|	   Multiplier.java
│      PowerFunc.java
│      Constant.java
│      Sin.java
│      Cos.java
│      MyFunc.java
│      Sum.java
│      Standard.java
│      
└─parser
        Lexer.java
        Parser.java

关于重构

架构

​ 由于上理论的时候，老师不断强调，对于例如1+2+3这样的表达式，我们可以把1，2，3分别看成一个整体；也可以把1+2看成一个整体，3看成一个整体；最后1+2+3也可以看成一个整体.

​ 再结合指导书对于架构设计的建议：

• 对于每一种函数（常数、幂函数、三角函数、求和函数、自定义函数），分别建立类
• 对于每一种运算规则（乘法、加减法），分别建立类
• 对于自定义函数，可以先将其 定义表达式 展开，将展开后的结果代入进行计算。
• 对于求和函数，可以类似于自定义函数进行代入

​ 于是，我一共定义了8个函数类，分别为加法类（Adder）、乘法类（Multiplier）、幂函数类（PowerFunc）、常量类（Constant）、正弦函数类（Sin）、余弦函数类（Cos），他们实现了Function接口

化简

Adder类化简核心代码（只包含主要逻辑）如下：
public Adder simplify() {
	for (Function func : functions) {
		if (func instance of Adder) {
			tmpFunctions = ((Adder) func).simplify().getFunctions();
			simFunctions.add(tmpFunctions);
		} else if (func instanceof Multiplier) {
			tmpFunction = ((Multiplier) func).simplify();
            for (Function func1 : tmpFunction.getFunctions() {
            	if (func1 instanceof Adder) {
            		tmpFunctions = ((Adder) func1).simplify().getFunctions();
            	} else {
            		tmpFunctions.add(func1);
            	}
            }
		}
	}
}

Multiplier类化简核心代码（只包含主要逻辑）如下：
public Adder simplify() {
        for (Function func : functions
        ) {
            if (addFunctions.isEmpty()) {
                if (func instanceof Adder) {
                    tmpFunction = ((Adder) func).simplify();
                    addFunctions.addAll(tmpFunction.getFunctions());
                } else if (func instanceof Multiplier) {
                    tmpFunction = ((Multiplier) func).simplify();
                    addFunctions.addAll(tmpFunction.getFunctions());
                } else {
                    addFunctions.add(func);
                }
            } else {
                if (func instanceof Adder) {
                    tmpFunction = ((Adder) func).simplify();
                    multiFunctions.addAll(tmpFunction.getFunctions());
                } else if (func instanceof Multiplier) {
                    tmpFunction = ((Multiplier) func).simplify();
                    multiFunctions.addAll(tmpFunction.getFunctions());
                } else {
                    multiFunctions.add(func);
                }
                addFunctions = multi(addFunctions, multiFunctions);
            }
        }
        return new Adder(addFunctions);
 }

合并

​ 为了能够更好地合并同类项，我单独建了一个Standard类（成员变量如图），可以表示随后化简表达式的每一个项，即形式为a\*x\*\*b\*[sin(inner)^c]*\*[cos(x)**d]*

​ 然后在Adder类新建一个HashMap，键值key为Standard类的对象，值value为该Standard的系数，也就是上式中的a，然后遍历Adder下的functions（未化简的项，可以想象每个function默认由加号连接组成表达式），对其包含的每个项进行合并，这里的合并体现在代码上就是对比HashMap的键值，如果不存在，则直接存入；如果存在，则更新该项的value（即更新该项的系数）

​ 其中注意，对于HashMap中的键值，为了保证能够真正意义合并同类项，需要重写HashCode，我们只需要保证power，sins和coss一致，就能确定是统一形式的项

​ 还有一点需要注意，这里重写HashCode，对于其中的sins，coss由于含有inner，即三角函数中的因子，所以对于每一个function的子类都需要重写一下HashCode来保证真正意义合并同类项

对于我所说的真正意义合并同类项，举个例子，比如sin((x+x))和sin((2*x)),由于表现形式不太一样，如果不重写HashCode会导致这两个生成的HashCode不一样，从而无法合并

迭代开发

在以上重构了的基础上，已经能够很好地满足第一次的要求，并且能够很方便地进行第二次作业的迭代开发。于是，针对第二次新加的自定义函数和求和函数，基本上只用解决表达式解析部分的改动，后面的化简与合并其实并不会影响到，这也体现了目前这一版本的架构的可扩展性

这一次作业作业新增了sin和cos以及自定义函数和求和函数，对于解析部分，新增sin和cos只需要在解析时识别到sin或cos的token以后，调用parseFactor对内部进行解析即可（这个已经能够支撑第三次作业对sin和cos的inner解析了）；而新增自定义函数和求和函数在这次作业中我选择了在字符串中进行暴力替换（虽然知道很不好，但当时还是这么做了）

对于自定义函数，当字符串解析时识别到f|g|h，把自定义函数调用这一部分提取出来，然后利用正则的捕获组提取出函数调用部分，再把对应部分进行替换，这里替换需要注意的是替换的顺序，如果自变量中含有x，需要先把x的部分替换以后再进行后续替换，否则如果遇到f(y,x)=y-x时如果按照自变量出现的顺序进行替换，就会出现y-x——>x-x，显然这样是错误的

对于求和函数，由于是sum(i,begin,end,..)的固定模式，直接把后面求和表达式中出现的i用begin逐渐+1知道begin进行替换。这个地方有四个坑点

• 第一个是在替换i的时候，由于求和表达式中肯能出现正弦函数sin，所以这里的i也会被替换掉，导致字符串不能正常解析（这也证实了进行字符串暴力替换的弊端)
• 第二个是begin，end是常量因子，所以我们需要把记录遍历到的序号时用BigInteger来存储，否则会数据溢出
• 第三个是要特判begin>end情况，输出为0
• 第四个是，如果直接字符串替换i，需要替换时在i两边加上括号，这个是我第三次强测以后才发现的问题，否则如果替换的数是负数时，会导致负号的作用范围扩大到整个项

Task3架构

由于此次作业仅在第二次作业的基础上做了少量的修改，所以这里只对修改部分进行描述

由于这一次作业自定义函数的实参可以是求和函数、表达式因子也可以是自定义函数，函数可以互相调用，所以如果还是使用第二次作业的暴力替换法的话就不太能醒得通了，而且容易引入很多奇怪的bug，于是我对表达式解析部分进行了修改，不在使用暴力替换，而是同样采用递归下降法来解析，当识别到f|g|h或者sum以后，对其函数调用或求和表达式对parseExpression进行再次调用，这样就只能保证表达式能够解析到最简形式然后不断返回

基于度量分析

前置知识

• ev(G) 基本复杂度是用来衡量程序非结构化程度的，非结构成分降低了程序的质量，增加了代码的维护难度，使程序难于理解。因此，基本复杂度高意味着非结构化程度高，难以模块化和维护。实际上，消除了一个错误有时会引起其他的错误。

• iv(G) 模块设计复杂度是用来衡量模块判定结构，即模块和其他模块的调用关系。软件模块设计复杂度高意味模块耦合度高，这将导致模块难于隔离、维护和复用。模块设计复杂度是从模块流程图中移去那些不包含调用子模块的判定和循环结构后得出的圈复杂度，因此模块设计复杂度不能大于圈复杂度，通常是远小于圈复杂度。

• v(G) 是用来衡量一个模块判定结构的复杂程度，数量上表现为独立路径的条数，即合理的预防错误所需测试的最少路径条数，圈复杂度大说明程序代码可能质量低且难于测试和维护，经验表明，程序的可能错误和高的圈复杂度有着很大关系。

TASK1

代码规模分析

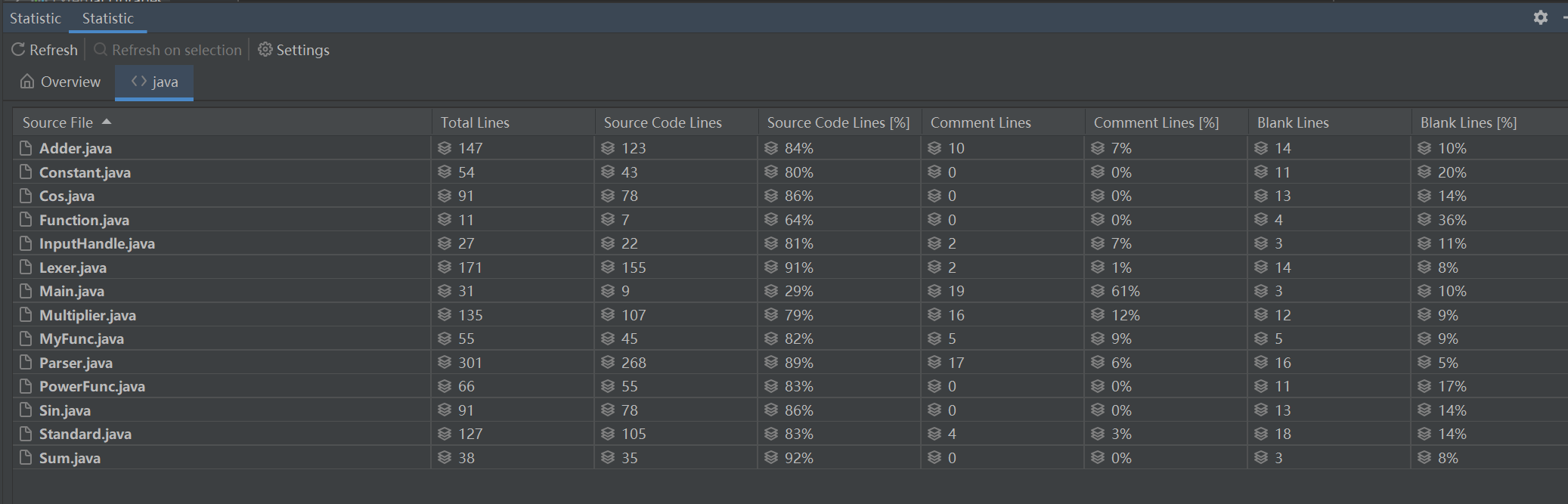
相比之下，用于表达式解析的Parser类和Lexer类代码量较多，显得较为臃肿，而其他关于表达式架构存储的类规模较为均衡

方法复杂度分析

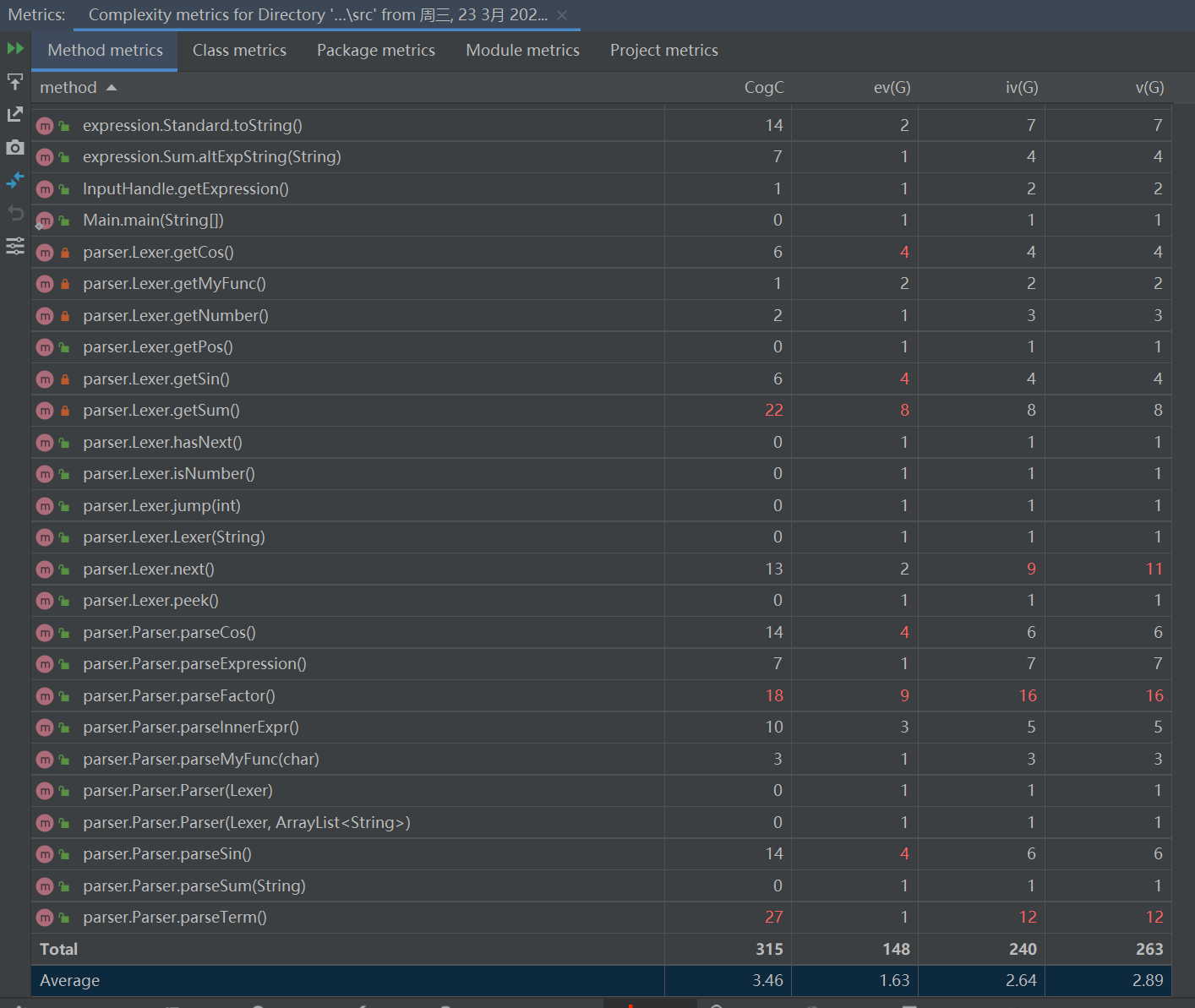
纵观所有方法，也就是在parser和lexer中出现了爆红，这从上面的代码规模中这两个类较为臃肿也就可以预料到

类复杂度分析

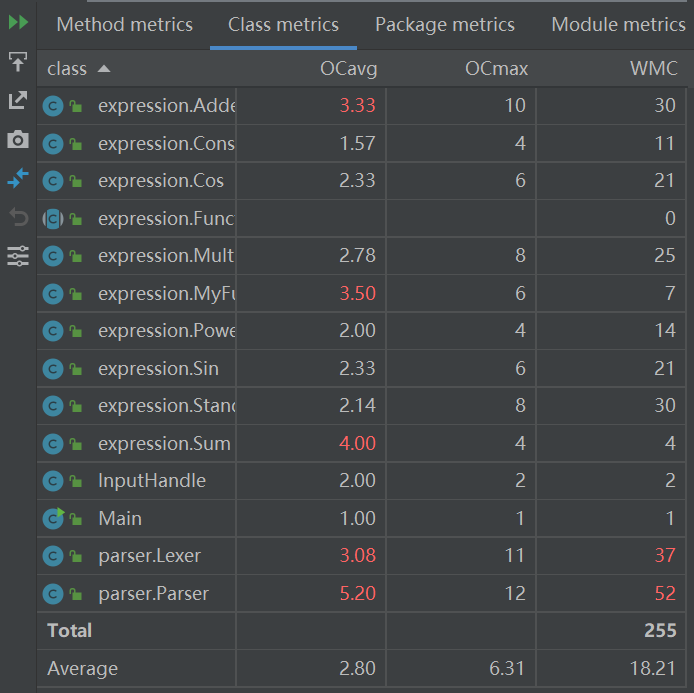
TASK2与TASK3

由于第三次作业在第二次作业上迭代开发，且仅进行了表达式解析部分的少量调整，所以直接对第三次作业进行度量分析

代码规模分析

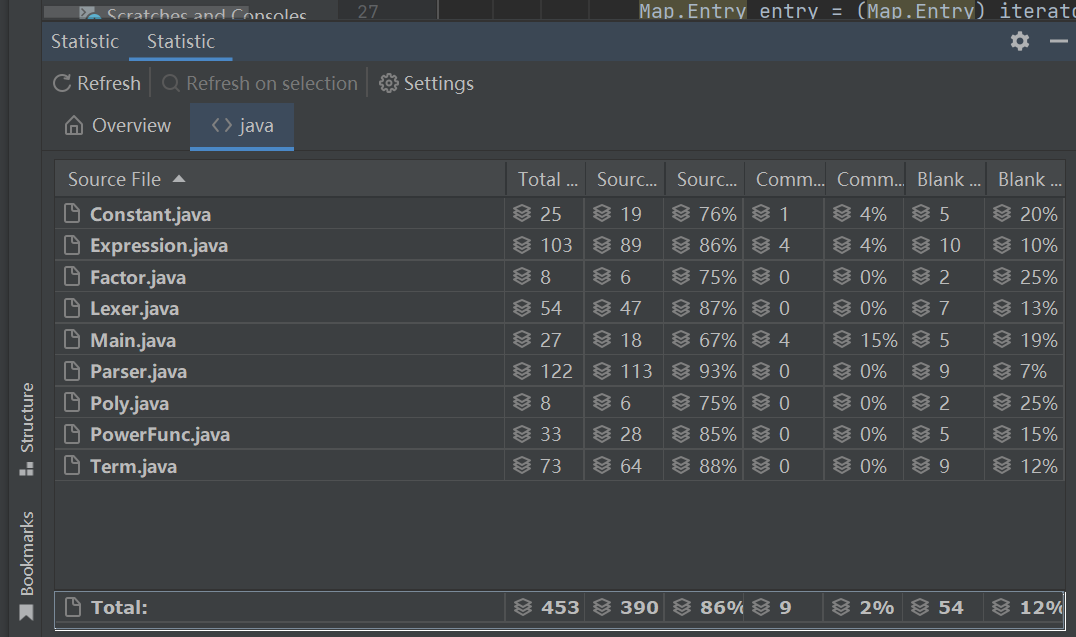
方法复杂度分析

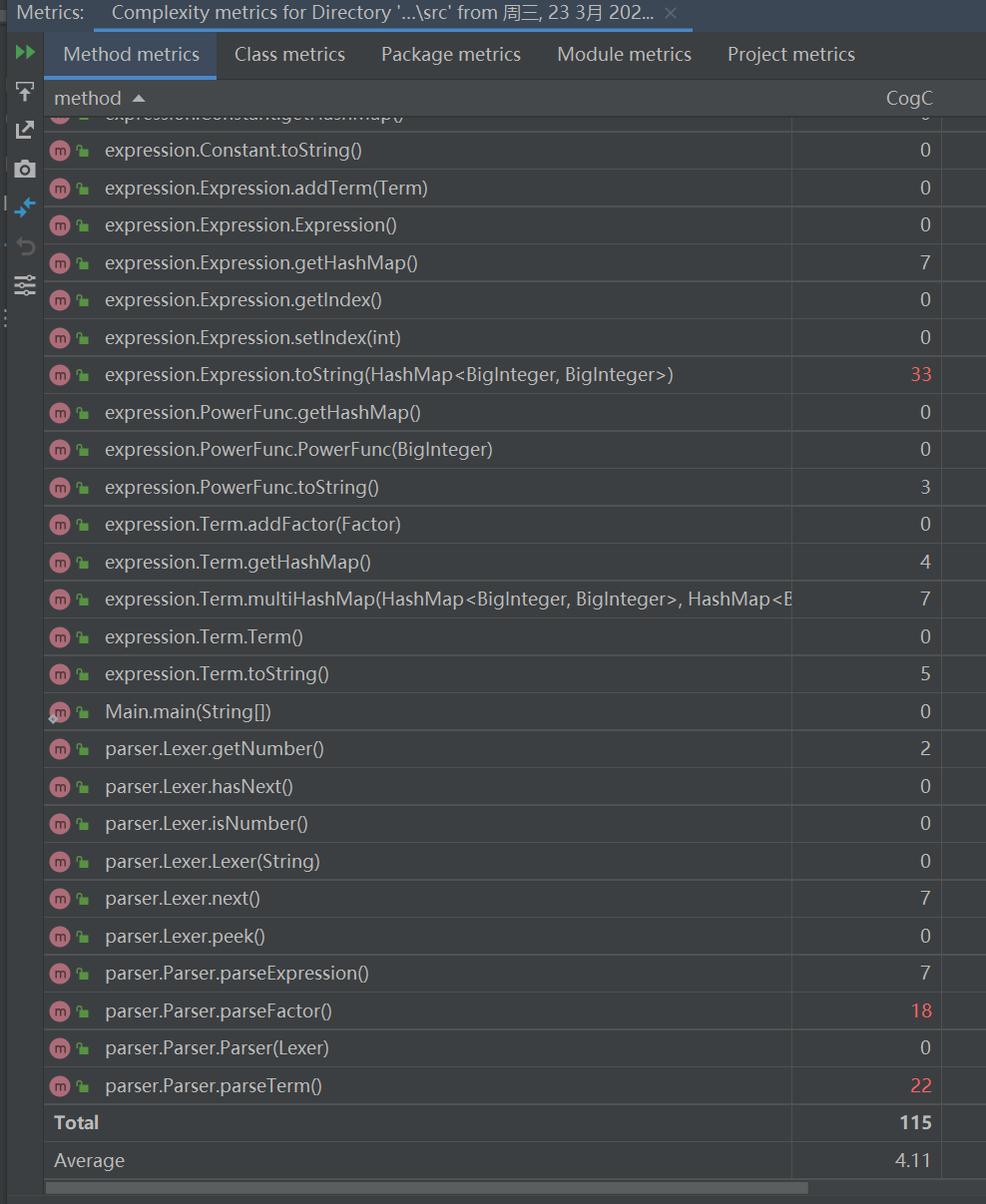
类复杂度分析

分析自己程序的bug

TASK1

这一次被强测和互测以后发现了一个bug，死于优化，经一次提交修复所有

输入：(+-x*0*-3)，输出：00*x

看起来问题很大的样子，其实就是因为遇到系数是0的项没有用加号分隔

TASK2

这一次强测错了一个点，互测没有被hack出bug，经一次提交修复所有

输入：

2
f(x,y,z)= (x)**+000-(cos(z)**2)**2
g(x)= +0-1009
(f(-0,sin(x),+0))**+02-sin(x**2)**+1 +-2-sum(i,1,10,(i*x))

输出

-1+-55*x+-2*cos(0)**4+1*cos(0)**8+-1*sin(x*x)

原因是对于sin内部因子的打印，我选择调用该因子的toSting()，而由于为了优化，将幂函数x**2简化为x*x，而本次作业对输出的要求是三角函数中只能包含幂函数或常量，所以输出错误

TASK3

这一次强测和互测出来归因于两个bug，但是在5行内修复了这两个bug，经过这三次懊悔于提交前没有好好测试

• 第一个：

  • 输入：

  0
  -+0 +-x*sin(cos((1-1)))**+2+sin((-sum(i,1,1,i)))
  

  • 输出：

  sin((-1))+-x*sin(cos(()))**2
  

  • 由于为了优化，对于Adder类的输出，当判断某一个标准项的系数为0时，直接return不输出，继续输出下一个标准项，忘记了

• 第二个：

  • 输入：

  0
  sum(i,-1,1,i**2)
  

  • 输出：空
  • 一方面由于本来就错误的输出为0，导致输出为空。另一方面，在对sum进行解析的时候，没有考虑到负数代入的情况，没有加括号，导致最后结果为-1**2+1**2=0

分析别人程序的bug

TASK1

/*第一个*/
输入：
-(0)+1
输出：0+-1*x**0
原因：符号的处理部分不对，负号作用到了后面的1
/*第二个*/
输入：1
输出：报错
原因：该同学选择了预解析模式，对于只有一个常量输入时，没有正确获取信息
/*第三个*/
输入：+-(-x-+-2)**1*x+(+-x*0*-3)*(-+x**1*0+x**+1)**3*+2
输出：-2*x+x**2+
原因：对于加号连接的时候最后一项为0时省略了0但是仍有加号输出

TASK2

输入：
0
sum(i,9999999999999999,10000000000000000,i*x)
输出：报错
原因：对于sum

TASK3

/*第一个*/
输入：
0
x*(sum(i,2,1,(sin(x)+1)))
输出：报错
原因：不能解析begin>end的情况
/*第二个*/
输入：
0
cos(0)
输出：0
原因：为了优化把cos(0)直接误判为输出0
/*第三个*/
输入：
0
sum(i,9999999999,10000000000,1)
输出：报错
原因：用Integer来存begin，end造成数据溢出

架构设计体验

​ 首先，很感谢课程组第一次训练给出的递归下降的框架，正是对这一框架的扩充让整个程序在解析字符串方面已经有很高的的鲁棒性。

​ 其次，从第一次到第二次作业为了后续更好的迭代进行了重构，事实证明重构并不是什么坏事，当发现原有框架不能满足现有需求时果断选择重构才能将损失降到最小，否则后期在原有框架上不断调整，终有一个时刻会坍塌。

​ 最后，由于我最后强测和互测发现的bug都是由于自己没有在提交前对输出部分进行严谨的审查，导致优化后出现了一些简单到不能再简单的bug。所以三次作业的bug修复我几乎都是在互测时候hack别人的时候发现了自己的低级错误，并都在修复开放后5行之内解决掉bug。虽然修复bug很快速，但是这些低级错误真的应该在中测结束前就自己解决掉。

​ 下周就到多线程了，希望能够在繁忙的四月也能很好地完成OO的课程任务。

​ 最后，如果本博客出现笔误或错误，欢迎批评指正！