基础矩阵知识 旋转-平移-投影-缩放-LookAt

在学习之前我默认我们有基本的线性代数认识。

计算机图形学基础

领域：计算机科学

关键概念：
• 坐标系
• 矩阵变换
• 三维投影

计算机图形学数学基础

目录

1. 笛卡尔坐标系
2. 齐次坐标系
3. 基础变换矩阵

笛卡尔坐标系

笛卡尔坐标系（Cartesian coordinate system）由法国数学家笛卡尔于1637年提出

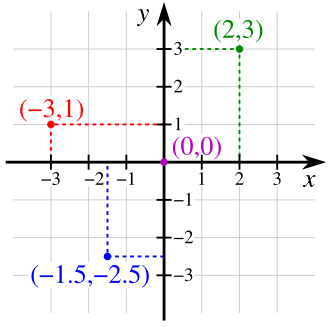
如图 ：直角坐标系。图中四点的坐标分别为，

绿点：(2, 3)，红点：(−3, 1)，

蓝点：(−1.5, −2.5)，紫点：(0, 0)。

当然我们的GLGS中一般使用的是三维笛卡尔坐标系。一般使用VEC3做表示

数学表示

二维坐标系中的点表示为：
P = (x, y) ∈ ℝ²

齐次坐标系

齐次坐标（Homogeneous coordinates）由August Ferdinand Möbius于1827年提出

其实目的就是为了更方向的在图形学上做计算。在GLGS中我们用VEC4做表示。

如下图：

坐标转换示例

笛卡尔坐标	→ 齐次坐标
(x, y)	(x, y, 1)

这是个有趣的一点，我们先不讨论齐次坐标系是什么，那为什么要加一个这样的多一个位数呢？

我们思考这样一件事，如果只用笛卡尔坐标系。我们或许很容易对其做平移,旋转，变换。

缩放
[[1*dx,0]  *  [[x] = [[x*dx]
[0,1*dx]]     [y]]    [y*dy]]
新的向量 [x*dy,y*dy]
示例：
dx=2, dy=0.5，向量(3,4) 缩放后为：
(3×2,4×0.5)=(6,2)
旋转
[[cosθ,-sinθ]  *  [[x] = [[x′]
[sinθ,cosθ]]     [y]]    [y′]]
旋转我们需要这样理解一下原式如何求得。
首先我们认为 x′=rcos(α) ,y′= rsin⁡(α+θ)
x′=rcos(α+θ)=r(cosαcosθ−sinαsinθ)=xcosθ−ysinθ
y′=rsin⁡(α+θ)=r(sin⁡αcos⁡θ+cos⁡αsin⁡θ)=xsin⁡θ+ycosθ

但是你会发现，它难以做平移和旋转。（注意先平移后旋转和先旋转再平移完全是两个结果）

需要一个加发和一个旋转乘法，这里我就不再赘述了。

那么如果加上一坐标系，这个坐标系并不对原本坐标系发生转变，但在计算的时候可以对其有较方便的影响，所以我们将使用其次坐标系去解决问题。

基础变换矩阵

平移矩阵

1	0	tx
0	1	ty
0	0	1

如上齐次坐标：
我们做简单的平移
[[1,0,tx],   [[x]    [[x*1+0+tx],
[0,1,ty],  * [y]   = [0+y*1+ty],
[0,0,1]]     [1]]    [0+0+1   ]]

这里我们发现，它可以平移了！齐次方程真的很方便。

三维旋转矩阵

 

三维旋转矩阵（齐次坐标）

1. 绕X轴旋转（角度θ）

1	0	0	0
0	cosθ	-sinθ	0
0	sinθ	cosθ	0
0	0	0	1

实例：绕X轴旋转90°

点 P = (0, 1, 0) 的齐次坐标为 [0, 1, 0, 1]^T

1	0	0	0
0	0	-1	0
0	1	0	0
0	0	0	1

计算结果：

0

0

1

1

→ 变换后坐标 P' = (0, 0, 1)

2. 绕Y轴旋转（角度θ）

cosθ	0	sinθ	0
0	1	0	0
-sinθ	0	cosθ	0
0	0	0	1

实例：绕Y轴旋转90°

点 P = (1, 0, 0) 的齐次坐标为 [1, 0, 0, 1]^T

0	0	1	0
0	1	0	0
-1	0	0	0
0	0	0	1

计算结果：

0

0

-1

1

→ 变换后坐标 P' = (0, 0, -1)

3. 绕Z轴旋转（角度θ）

cosθ	-sinθ	0	0
sinθ	cosθ	0	0
0	0	1	0
0	0	0	1

实例：绕Z轴旋转90°

点 P = (1, 0, 0) 的齐次坐标为 [1, 0, 0, 1]^T

0	-1	0	0
1	0	0	0
0	0	1	0
0	0	0	1

计算结果：

0

1

0

1

→ 变换后坐标 P' = (0, 1, 0)

关键点总结

• 齐次坐标通过添加第四维（值为1）统一变换操作
• 旋转矩阵第四行固定为 [0, 0, 0, 1]
• 遵循右手旋转法则（拇指指向轴的正方向）

这里我直接承接平移一个新的承接旋转平移的方法。
例如对点对其向量 （1，0，1，1） 平移 x->2,y->3,并绕着y轴旋转60°，我们可以只用一个矩阵解决
[cosθ, 0  ,sinθ,2  ]
[0    , 1  ,  0 ,3   ]
[-sinθ,0  ,cosθ,0 ]
[ 0, 0, 0, 1 ]

后面我们会学习一种叫做欧拉角和四元数的旋转矩阵，这将更为方便使用。

LookAt矩阵

这是一种专注于目标点和相机本身的一种矩阵。围绕目标点做矩阵变换。

viewMatrix = [
    [Rx, Ry, Rz, -eye·R],
    [Ux, Uy, Uz, -eye·U],
    [Dx, Dy, Dz, -eye·D],
    [0,   0,  0,       1]
]