并查集

并查集模板：

#include <iostream>
#include <vector>

using namespace std;

// 初始化父节点数组
vector<int> fa;

// 查找根节点并进行路径压缩
int findParent(int x) {
    if (x == fa[x]) return x;
    return fa[x] = findParent(fa[x]);
}

// 合并两个集合
void unionSets(int x, int y) {
    fa[findParent(x)] = findParent(y);
}

// 初始化并查集
void initialize(int n) {
    fa.resize(n);
    for (int i = 0; i < n; ++i) {
        fa[i] = i;
    }
}

int main() {
    int n = 10; // 假设有10个元素
    initialize(n);

    // 示例操作
    unionSets(1, 2);
    unionSets(3, 4);
    unionSets(2, 4);

    // 检查是否在同一个集合中
    if (findParent(1) == findParent(3)) {
        cout << "1 and 3 are in the same set." << endl;
    } else {
        cout << "1 and 3 are in different sets." << endl;
    }

    if (findParent(1) == findParent(5)) {
        cout << "1 and 5 are in the same set." << endl;
    } else {
        cout << "1 and 5 are in different sets." << endl;
    }

    return 0;
}

其实这里有个核心思想，并查集它在干一件事，那就是分集；在find的时候知道它在那个集合中。

那么看以下例题

P1955 [NOI2015] 程序自动分析 - 洛谷 | 计算机科学教育新生态

题目描述

在实现程序自动分析的过程中，常常需要判定一些约束条件是否能被同时满足。

考虑一个约束满足问题的简化版本：假设 $x_{1}, x_{2}, x_{3}, \dots$ 代表程序中出现的变量，给定 $n$ 个形如 $x_{i} = x_{j}$ 或 $x_{i} \neq = x_{j}$ 的变量相等/不等的约束条件，请判定是否可以分别为每一个变量赋予恰当的值，使得上述所有约束条件同时被满足。例如，一个问题中的约束条件为： $x_{1} = x_{2}, x_{2} = x_{3}, x_{3} = x_{4}, x_{4} \neq = x_{1}$ ，这些约束条件显然是不可能同时被满足的，因此这个问题应判定为不可被满足。

现在给出一些约束满足问题，请分别对它们进行判定。

输入格式

输入的第一行包含一个正整数 $t$ ，表示需要判定的问题个数。注意这些问题之间是相互独立的。

对于每个问题，包含若干行：

第一行包含一个正整数 $n$ ，表示该问题中需要被满足的约束条件个数。接下来 $n$ 行，每行包括三个整数 $i, j, e$ ，描述一个相等/不等的约束条件，相邻整数之间用单个空格隔开。若 $e = 1$ ，则该约束条件为 $x_{i} = x_{j}$ 。若 $e = 0$ ，则该约束条件为 $x_{i} \neq = x_{j}$ 。

输出格式

输出包括 $t$ 行。

输出文件的第 $k$ 行输出一个字符串 YES 或者 NO（字母全部大写），YES 表示输入中的第 $k$ 个问题判定为可以被满足，NO 表示不可被满足。

输入输出样例

输入 #1

输出 #1

NO
YES

输入 #2

输出 #2

YES
NO

看完题目我们其实就知道可以划分为，xi=xj在其中一个子集中，xi！=xj在另一个子集中，那么我们只需要建立一个子集xi=xj，并查找子集中是否如果其中存在xi！=xj

那么我们可以写以下代码

#include<iostream>
#include<algorithm>
#include<cstring>
#include<unordered_map>
#include<vector>
using namespace std;
const long long N = 1e5 + 10;
long long n, k;
long long p[N*2];
unordered_map<long long, long long> mp;
vector<pair<long long, long long>> query;

long long find(long long x) {
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

void merge(long long x, long long y) {
    long long pa = find(x), pb = find(y);
    if (pa != pb) p[pa] = pb;
}

int main() {
    int T;
    cin >> T;
    while (T--) {
        cin >> n;
        k = 0;
        mp.clear();
        query.clear();
        for (long long i = 1; i < N*2; i++) {
            p[i] = i;
        }
        while (n--) {
            long long a, b, e;
            cin >> a >> b >> e;
            if (e == 1) merge(a, b);
            else query.push_back({ a, b });
        }
        bool vis = true;
        for (long long i = 0; i < query.size(); i++) {
            long long a = query[i].first, b = query[i].second;
            if (find(a) == find(b)) {
                vis = false;
                break;
            }
        }

        if (vis) puts("YES");
        else puts("NO");
    }
    return 0;
}

经典例题：食物链

P2024 [NOI2001] 食物链 - 洛谷 | 计算机科学教育新生态

题目描述

动物王国中有三类动物 $A, B, C$ ，这三类动物的食物链构成了有趣的环形。 $A$ 吃 $B$ ， $B$ 吃 $C$ ， $C$ 吃 $A$ 。

现有 $N$ 个动物，以 $1 \sim N$ 编号。每个动物都是 $A, B, C$ 中的一种，但是我们并不知道它到底是哪一种。

有人用两种说法对这 $N$ 个动物所构成的食物链关系进行描述：

第一种说法是 1 X Y，表示 $X$ 和 $Y$ 是同类。
第二种说法是2 X Y，表示 $X$ 吃 $Y$ 。

此人对 $N$ 个动物，用上述两种说法，一句接一句地说出 $K$ 句话，这 $K$ 句话有的是真的，有的是假的。当一句话满足下列三条之一时，这句话就是假话，否则就是真话。

当前的话与前面的某些真的话冲突，就是假话；
当前的话中 $X$ 或 $Y$ 比 $N$ 大，就是假话；
当前的话表示 $X$ 吃 $X$ ，就是假话。

你的任务是根据给定的 $N$ 和 $K$ 句话，输出假话的总数。

输入格式

第一行两个整数， $N, K$ ，表示有 $N$ 个动物， $K$ 句话。

第二行开始每行一句话（按照题目要求，见样例）

输出格式

一行，一个整数，表示假话的总数。

输入输出样例

输入 #1

输出 #1

拓展域：

#include <bits/stdc++.h> //万能头 
using namespace std;
int fa[300001];
//并查集 
int find(int x)//查找 
{
	if(x != fa[x])
	{
		fa[x] = find(fa[x]);
	}
	return fa[x];
}
int unity(int x, int y)//合并 
{
	int r1 = find(fa[x]);
	int r2 = find(fa[y]);
	fa[r1] = r2;
}
int main()
{
	int i, n, k, x, y, z;
	int ans = 0;
	cin >> n >> k; // 输入 
	for(i = 1; i <= 3 * n; i++) // 初始化 
	{
		fa[i] = i; 
	}
	// x是同类，x + n是猎物， x + 2 * n是天敌 
	for(i = 1; i <= k; i++)
	{
		cin >> z >> x >> y;
		if(x > n || y > n) // x和y不能大于n 
		{
			ans++; // 假话++ 
		}
		else
		{
			if(z == 1) // x和y是同类 
			{
				if(find(x + n) == find(y) || find(x + 2 * n) == find(y)) // 如果是同类，x不能是y的猎物或天敌 
				{
					ans++; // 假话++ 
				}
				else
				{
					unity(x, y); // x的同类是y的同类 
					unity(x + n, y + n); // x的猎物是y的猎物
					unity(x + 2 * n, y + 2 * n); // x的天敌是y的天敌 
				}
			}
			else // y是x的猎物 
			{
				if(x == y || find(x) == find(y) || find(x + 2 * n) == find(y)) // 如果y是x的猎物，x不能是y的猎物，x不能和y是同类，y不能是x的天敌 
				{
					ans++; // 假话++ 
				}
				else
				{
					unity(x, y + 2 * n); // x的同类是y的天敌 
					unity(x + n, y); // x的猎物是y的同类
					unity(x + 2 * n, y + n); // x的天敌是y的猎物
				}
			}
		}
	}
	cout << ans; // 输出 
	return 0;
}

带权边：

C125【模板】带权并查集 P2024 [NOI2001] 食物链_哔哩哔哩_bilibili

// 带权并查集
#include <iostream>
using namespace std;

const int N=50005;
int n,m,k,x,y,ans;
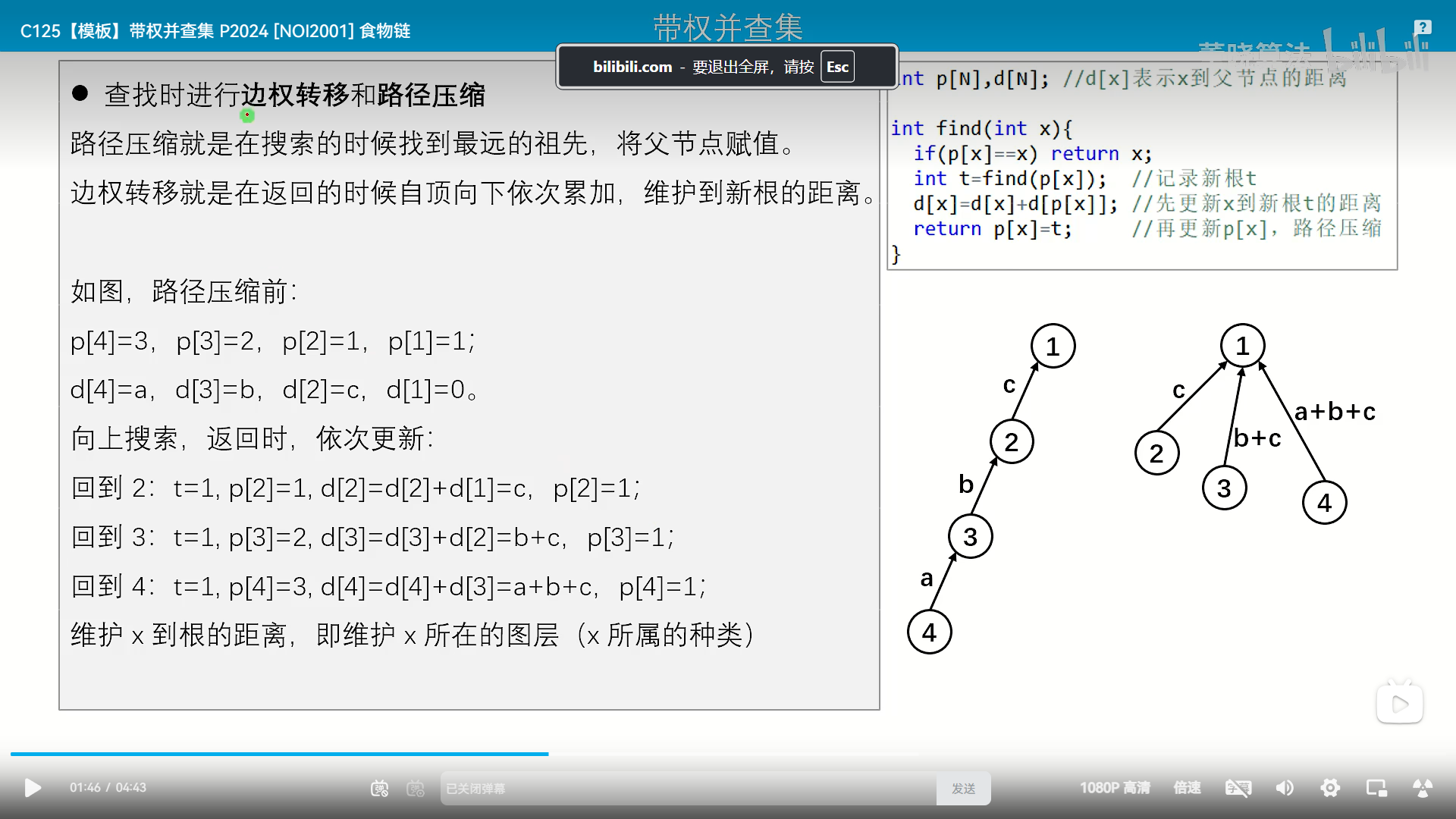
int p[N],d[N]; //d[x]表示x到根的距离

int find(int x){
  if(p[x]==x) return x;
  int t=find(p[x]);  //记录新根t
  d[x]=d[x]+d[p[x]]; //先更新x到新根t的距离
  return p[x]=t;     //再更新p[x]，路径压缩
}
int main(){
  scanf("%d%d",&n,&m);
  for(int i=1; i<=n; i++) p[i]=i;
  while(m--){
    scanf("%d%d%d",&k,&x,&y);
    int px=find(x),py=find(y);
    if(x>n||y>n) ans++;
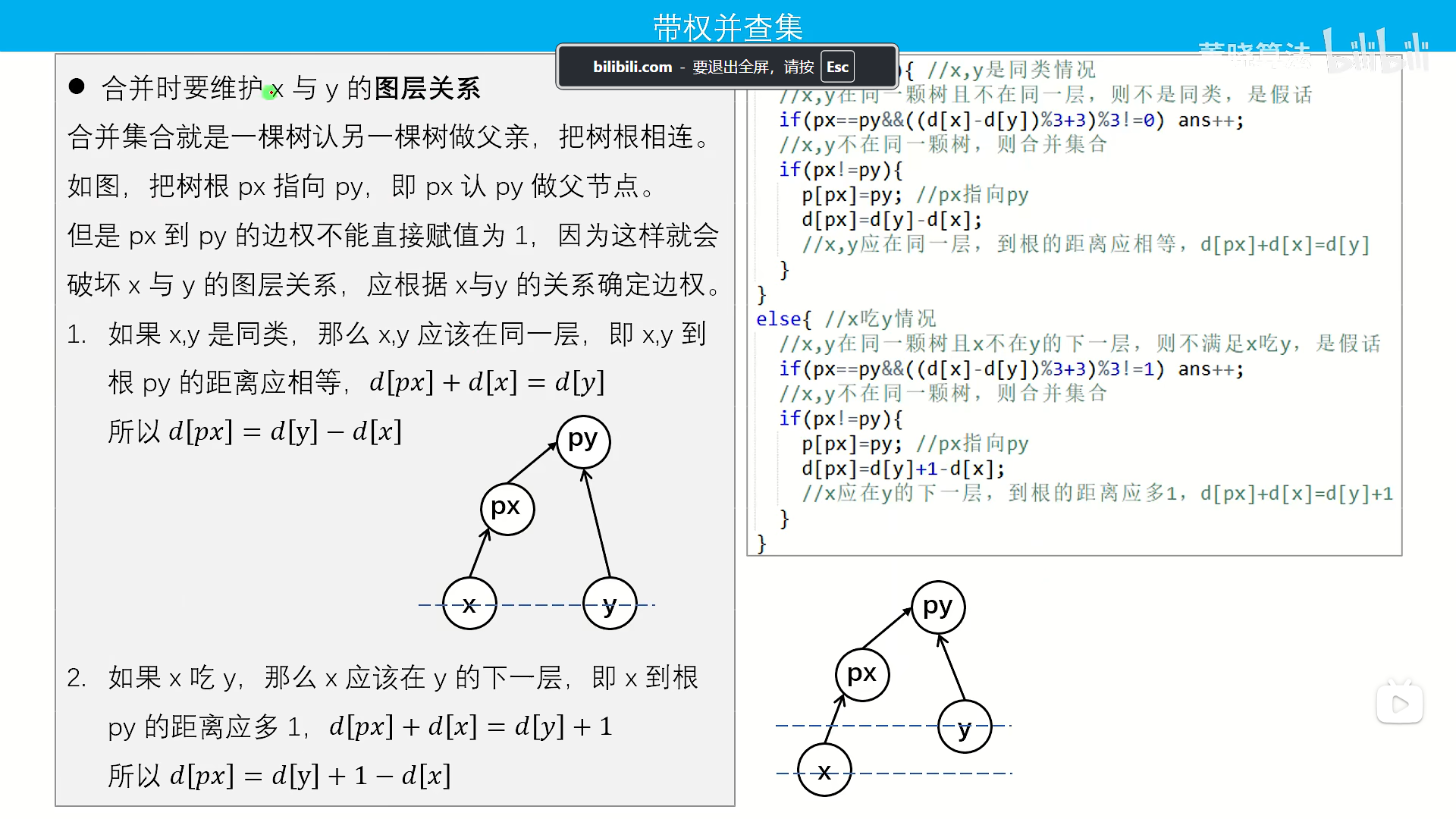
    else if(k==1){ //x,y是同类情况
      //x,y在同一颗树且不在同一层，则不是同类，是假话
      if(px==py&&((d[x]-d[y])%3+3)%3!=0) ans++;
      //x,y不在同一颗树，则合并集合
      if(px!=py){ 
        p[px]=py; //px指向py
        d[px]=d[y]-d[x]; 
        //x,y应在同一层，到根的距离应相等，d[px]+d[x]=d[y]
      }
    }
    else{ //x吃y情况
      //x,y在同一颗树且x不在y的下一层，则不满足x吃y，是假话
      if(px==py&&((d[x]-d[y])%3+3)%3!=1) ans++;
      //x,y不在同一颗树，则合并集合
      if(px!=py){
        p[px]=py; //px指向py
        d[px]=d[y]+1-d[x];
        //x应在y的下一层，到根的距离应多1，d[px]+d[x]=d[y]+1
      }           
    }
  }
  printf("%d\n",ans);
}

posted @ 2024-12-28 15:12 安娜アンナ阅读(21) 评论(0) 收藏举报

刷新页面返回顶部

AnnaStore

并查集

题目描述

输入格式

输出格式

输入输出样例

拓展域：

带权边：

公告