欧拉路径

1736年29岁的欧拉向圣彼得堡科学院递交了《哥尼斯堡的七座桥》的论文，在解答问题的同时，开创了数学的一个新的分支——图论与拓扑学，也由此展开了数学史上的新历程。

七桥问题提出后，很多人对此很感兴趣，纷纷进行试验，但在相当长的时间里，始终未能解决。欧拉通过对七桥问题的研究，不仅圆满地回答了哥尼斯堡居民提出的问题，而且得到并证明了更为广泛的有关一笔画的三条结论，人们通常称之为“欧拉定理F”。

 

 

我们来看一下七桥问题：

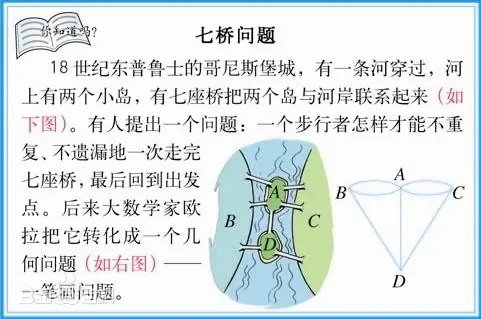
问题提出后，很多人对此很感兴趣，纷纷进行试验，但在相当长的时间里，始终未能解决。而利用普通数学知识，每座桥均走一次，那这七座桥所有的走法一共有7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040（种）。而这么多情况，要一一试验，这将会是很大的工作量。其实就是我们的DFS，这样看来虽然只有七次，但其搜索量依然巨大。

我们来看看七桥问题

P7771 【模板】欧拉路径 - 洛谷 | 计算机科学教育新生态

题目描述

求有向图字典序最小的欧拉路径。

输入格式

第一行两个整数 $n,m$ 表示有向图的点数和边数。

接下来 $m$ 行每行两个整数 $u,v$ 表示存在一条 $u\to v$ 的有向边。

输出格式

如果不存在欧拉路径，输出一行 No。

否则输出一行 $m+1$ 个数字，表示字典序最小的欧拉路径。

输入输出样例

输入 #1复制

4 6
1 3
2 1
4 2
3 3
1 2
3 4

输出 #1复制

1 2 1 3 3 4 2

输入 #2复制

5 5
1 2
3 5
4 3
3 4
2 3

输出 #2复制

1 2 3 4 3 5

输入 #3复制

4 3
1 2
1 3
1 4

输出 #3复制

No

很明显，这是一个欧拉路径问题，那么我们看看如何解决这个问题：
半欧拉图：具有欧拉路径但不具有欧拉回路的图

    无向图--有且仅有两个顶点入度是奇数

    有向图--有且仅有一个顶点（入度-出度）=1

    另有且仅有一个顶点（出度-入度）=1

 

OK所以做任何欧拉路径的时候我们都应该做一个简单判断：

    for (int i = 1; i <= n; i++) {
        if (du[i][1] != du[i][0]) {
            flag = 0;
            if (du[i][1] - du[i][0] == 1 ) cnt[1]++, S = i;
            else if (du[i][0] - du[i][1] == 1 ) cnt[0]++;
            else return puts("No"), 0;
        }
    }

接下来我们来看欧拉路径

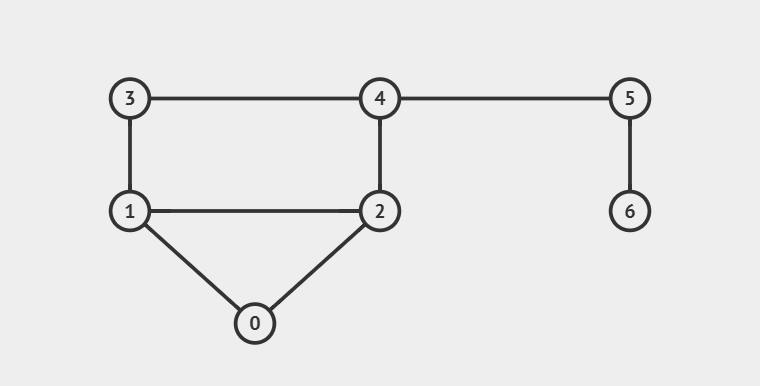
在这个图中，我们只需要从某节点开始遍历，接着每走完一步就删除其中的边，当走完某点所有边时候就将该节点放入栈

其中如何实现删除边呢，其实就是避免重复走，假设0点->2点，万一回到1点->0点，我们肯定不会从0点第一个边遍历吧，那么我们就从最后一次0走的边再次遍历。

那么我们可以用如下方式遍历整个图：

void dfs(int now) {
    for (int i = del[now]; i < G[now].size(); i = del[now]) {
        del[now] = i + 1;
        dfs(G[now][i]);
    }
    st.push(now);
}

其实这个就是核心路径。此时我们的欧拉路径问题已经解决。

而且我们发现，其中的时间复杂度为O(n);