第 3 节 全微分

第三节 全微分

一、全微分的定义

  由偏导数的定义知道，二元函数对某个自变量的偏导数表示当另一个自变量固定时，因变量相对于该自变量的变化率.根据一元函数微分学中增量与微分的关系，可得

  \(f(x+△x,y)-f(x,y)≈f_x(x,y)△x\),
  \(f(x,y+\triangle y)-f(x,y)≈f_y(x,y)\triangle y\).

  上面两式的左端分别叫做二元函数对 x 和对 y 的偏增量，而右端分别叫做二元函数对 x 和对 y 的偏微分.

  设函数 \(z=f(x,y)\) 在点 P(x,y) 的某邻域内有定义，\(P'(x+△x,y+△y)\) 为这邻域内的任意一点，则称这两点的函数值之差 \(f(x+△x,y+△y)-f(x,y)\) 为函数在点P对应于自变量增量 \(△x\) 和 \(△y\) 的全增量，记作 \(△z\), 即
\(△z=f(x+△x,y+△y)-f(x,y). \qquad(3-1)\)

定义 设函数 \(z=f(x,y)\) 在点 \((x,y)\) 的某邻域内有定义，如果函数在点 \((x,y)\) 的全增量
\(\qquad\qquad△z=f(x+△x,y+\triangle y)-f(x,y)\)
可表示为
\(\qquad\qquad△z=A△x+B△y+o(\rho), (3-2)\)
其中A 和B不依赖于 \(△x\) 和 \(\triangle y\) 而仅与 x 和 y 有关，\(\rho = \sqrt{(\triangle x)^2+(\triangle y)²}\), 那么称函数 \(z=f(x,y)\) 在点 \((x,y)\) 可微分，而 \(A\triangle x+B\triangle y\) 称为函数 \(z=f(x,y)\) 在点 \((x,y)\) 的全微分，记作 dz,即
\(\qquad dz=A△x+B△y\).

  如果函数在区域 D 内各点处都可微分，那么称这函数在 D 内可微分

函数在某点可微分，函数在某点一定连续.

定理1(必要条件) 如果函数 \(z=f(x,y)\) 在点 \((x,y)\) 可微分，那么该函数在点 \((x,y)\) 的偏导数 \(\Large \frac{\partial z}{\partial x}\) 和 \(\Large \frac{\partial z}{\partial y}\) 必定存在，且函数 \(z=f(x,y)\) 在点 \((x,y)\) 的全微分为

  \(dz={\Large \frac{\partial z}{\partial x}}\triangle x + {\Large \frac{\partial z}{\partial y}}\triangle y\).

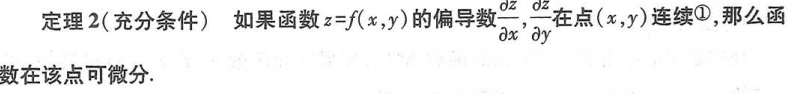
二、全微分在近似计算中的应用

绝对值的误差