第一节 不定积分的概念与性质

第一节 不定积分的概念与性质

一、原函数与不定积分的概念

定义1：
如果在区间 \(I\) 上，可导函数 \(F(x)\) 的导函数为 \(f(x)\), 即对任一 \(x\in I\), 都有 \(F′(x)=f(x)\) 或 \(dF(x)=f(x)dx\), 那么函数 \(F(x)\) 就称为 \(f(x)\) (或 \(f(x)dx\))在区间 \(I\)上的一个原函数.

---

原函数存在定理：
如果函数 \(f(x)\) 在区间 \(I\) 上连续，那么在区间 \(I\) 上存在可导函数 \(F(x)\), 使对任一 \(x \in I\) 都有
\(\qquad F′(x)=f(x)\).
简单地说就是：连续函数一定有原函数.

如果f(x)有一个原函数，那么f(x)就有无限多个原函数

---

---

  函数f(x)的原函数的图形称为f(x)的积分曲线，本例即是求函数y=2x 的通过点(1,2)的那条积分曲线. 显然，这条积分曲线可以由另一条积分曲线(例如y=x²)沿 y 轴方向平移而得

---

二、基本积分表

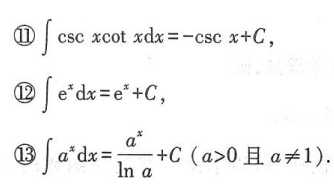
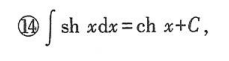
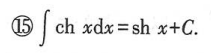
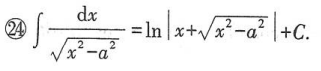
三、不定积分的性质