求导数总结
求导数方法总结
导数最后都要是包含 x 的表达式?
答题步骤参考第二节 例13、14
\(\Large \frac{dy}{dx}\) 是 y 对 x 的导数
\(\Large\frac{dx}{dy}\) 是 x 对 y 的导数
1. 基本求导法则与导数公式
-
常数的导数等于 0
-
幂函数的导数 \(f(x)=x^n, f'(x) = nx^{n-1}\)
-
指数函数的导数:\(f(x)=a^x (a>0, a\neq 1), f'(x) = a^x\ln a\)
-
三角函数:
- \((\sin x)'= \cos x\)
- \((\cos x)'=-\sin x\)
- \((\tan x)'=\sec^2 x\)
- \((\sec x)'=\sec x\tan x\)
-
对数函数的导数:\(f(x)=\log _a x(a>0, a\neq 1), f'(x)=\frac{1}{x\ln a}\)
-
幂指函数的导数
![img]()
上图中用的是复合函数的求导和函数的积的求导法则
2. 函数的和、差、积、商的求导法则
(1) \(\Large[u(x)±v(x)]'=u'(x)\pm v'(x)\);
(2) \(\Large[u(x)v(x)]'=u'(x)v(x)+u(x)v'(x)\);
(3) \(\large [\frac{u(x)}{vx}]'=\frac{u'(x)v(x)-u(x)v'(x)}{v^2(x)}(v(x)\neq 0)\)
3. 反函数的求导法则
4. 复合函数的求导法则


5. 两边同时取对数
高阶导数的求导

一级一级做下去。
y=f(x),
y'也是关于x 的函数,对这个函数再求一次导
常见初等函数的 n 阶导数
\((e^x)^{(n)}=e^x\)
\((\sin x)^{(n)}=\sin(x + n\cdot\frac{\pi}{2})\)
\((\cos x)^{(n)}=\cos(x+n\cdot \frac{\pi}{2})\)
\((x^\mu)^{(n)}=\mu(\mu-1)(\mu-2)\cdots(\mu-n+1)x^{\mu-n}\)
当 \(\mu = n\) 时,\((x^\mu)^{(n)}=n!\)
\((x^\mu)^{(n+k)}=0, (k = 1, 2, \cdots\) 因为常数的导数为 0
和、差的 n 阶导数
如果函数 \(u=u(x)\) 及 \(v=v(x)\) 都在点 x 处具有 n 阶导数,那么显然 \(u(x)+v(x)\) 及 \(u(x)-v(x)\) 也在点 x 处具有n 阶导数,且
\((u±v)^n=u^{(n)}±v^{(n)}\)
乘的 n 阶导数
乘积 \(u(x)v(x)\) 的 n 阶导数 是莱布尼茨公式
可以利用牛顿二项式定理的公式记忆
\((uv)^n=\sum_{k = 0} ^n{n \choose k}x^{n-k}y^k\)
n-k 和 k 表示 n-k 阶 和 k 阶导数(0 阶导数理解为函数本身)
隐函数求导
两边同时求导
由参数方程确定的函数的导数公式
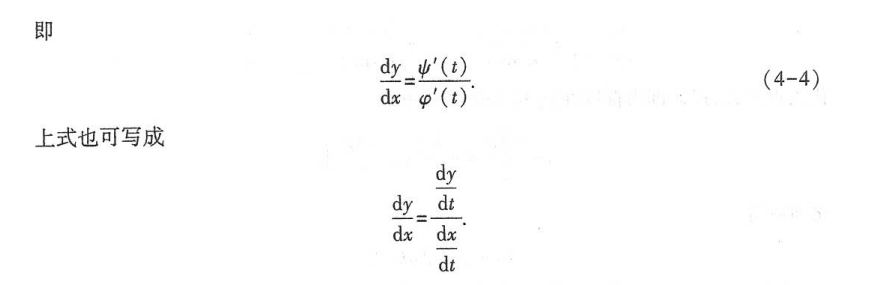


 浙公网安备 33010602011771号
浙公网安备 33010602011771号