第九节 连续函数的运算与初等函数的连续性

第九节 连续函数的运算与初等函数的连续性

一、连续函数和、差、积、商的连续性

定理1： 设函数 \(f(x)\) 和 \(g(x)\) 在点 \(x₀\) 连续，则它们的和(差)\(f±g\)、积\(f·g\)及商 \(\frac{f}{g}\) (当 \(g(x₀)≠0\) 时)都在点 x₀ 连续.

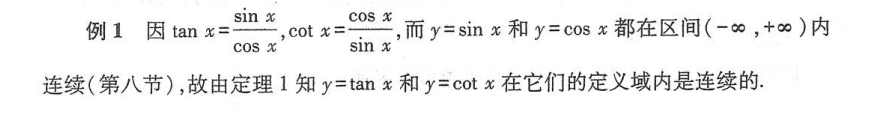
二、反函数与复合函数的连续性

定理2： 如果函数 \(y=f(x)\) 在区间 \(I_x\), 上单调增加(或单调减少)且连续，那么它的反函数 \(x=f(y)\) 也在对应的区间 \(I_y=\{y|y=f(x),x\in I_x\}\) 上单调增加(或单调减少)且连续

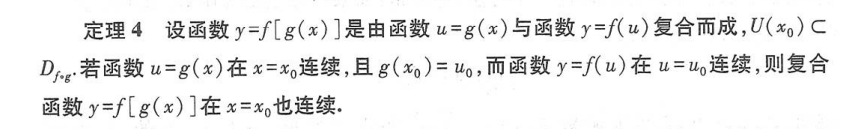
三、初等函数的连续性

基本初等函数在它们的定义域内都是连续的，最后，根据第一节中关于初等函数的定义，由基本初等函数的连续性以及本节定理1、定理4可得下列重要结论：一切初等函数在其定义区间内都是连续的，所谓定义区间，就是包含在定义域内的区间

  根据函数 \(f(x)\) 在点 \(x₀\) 连续的定义，如果已知 \(f(x)\) 在点 \(x₀\) 连续，那么求 \(f(x)\) 当 \(x→x₀\) 的极限时，只要求 \(f(x)\) 在点x₀ 的函数值就行了, 因此：
  如果 \(f(x)\) 是初等函数，且 \(x₀\) 是 \(f(x)\) 的定义区间内的点，那么

  \(\qquad \underset{x\rightarrow x_0}{\lim} f(x)=f(x_0)\)