Codeforces Global Round 19

A

#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int N = 1e5 + 10;
int n;
int a[N];
void solve()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ )  scanf("%d", &a[i]);
    for (int i = 2; i <= n; i ++ )
        if (a[i] < a[i - 1]) {
            puts("YES");
            return;
        }
    puts("NO");
}
int main() {
    int T;
    scanf("%d", &T);
    while (T -- )   solve();
    return 0;
}

B

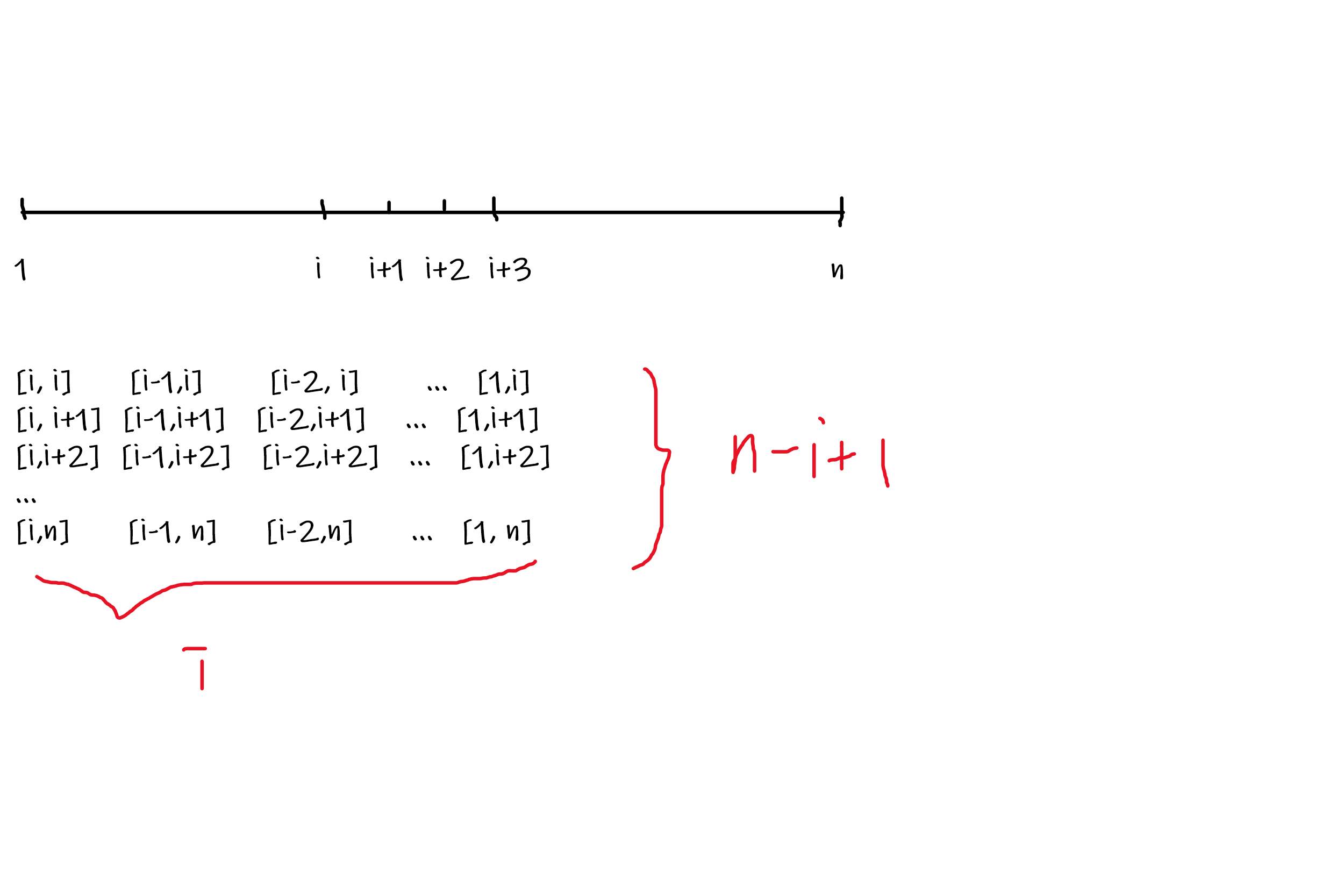
可以发现连续一段的最大值相当于把每个数都分成单独的序列所得到的贡献，所以每段序列的贡献值就为该子段的长度+该子段中\(0\)的个数
之后就可以通过枚举每个子段来计算
此时可以发现\(i\)这个点一共出现在\(i * (n - i + 1)\)个子段中，所以\(i\)这个点的贡献就为\(i * (n - i + 1)\)，而如果这个点为0的话在每个子段中的贡献还要多加\(1\)

#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int N = 1e5 + 10;
int n;
int a[N];
void solve()
{
    scanf("%d", &n);
    int res = 0;
    for (int i = 1; i <= n; i ++ )  scanf("%d", &a[i]);
    for (int i = 1; i <= n; i ++ ) {
        res += (n - i + 1) * i;
        if (a[i] == 0)  res += (n - i + 1) * i;
    }
    printf("%d\n", res);
}
int main() {
    int T;
    scanf("%d", &T);
    while (T -- )   solve();
    return 0;
}

C

#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int N = 1e5 + 10;
int n;
int a[N];
void solve()
{
    scanf("%d", &n);
    LL res = 0;
    int maxx = 0;
    for (int i = 1; i <= n; i ++ )  {
        scanf("%d", &a[i]);
        if (i != 1 && i != n)   maxx = max(maxx, a[i]);
    }
    if (n == 3) {
        if (a[2] % 2 == 0)  printf("%d\n", a[2] / 2);
        else printf("-1\n");
        return;
    }
    if (maxx == 1)  {printf("-1\n"); return;}
    for (int i = 2; i < n; i ++ )   
        if (a[i] % 2 == 0)  res += a[i] / 2;
        else res += a[i] / 2 + 1;
    printf("%lld\n", res);
}
int main() {
    int T;
    scanf("%d", &T);
    while (T -- )   solve();
    return 0;
}

D

#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int N = 1e4 + 10;
int n;
int a[N], b[N], f[100][N], sum_min[N], sum_max[N];
void solve()
{
    scanf("%d", &n);
    LL res = 0, tot = 0;
    memset(f, 0, sizeof f);
    for (int i = 1; i <= n; i ++ )  scanf("%d", &a[i]), res += a[i] * a[i] * (n - 2), tot += a[i];
    for (int i = 1; i <= n; i ++ )  scanf("%d", &b[i]), res += b[i] * b[i] * (n - 2), tot += b[i];
    for (int i = 1; i <= n; i ++ )  sum_min[i] = sum_min[i - 1] + min(a[i], b[i]), sum_max[i] = sum_max[i - 1] + max(a[i], b[i]);
    if (n == 1) {puts("0"); return;}
    f[0][0] = 1;
    for (int i = 1; i <= n; i ++ )
        for (int j = sum_min[i - 1]; j <= sum_max[i - 1]; j ++ )
            if (f[i - 1][j])    f[i][j + a[i]] = 1, f[i][j + b[i]] = 1;
    LL sum = 1e18;
    for (int i = sum_min[n]; i <= sum_max[n]; i ++ )
        if (f[n][i]) 
            sum = min(i * i + (tot - i) * (tot - i), sum);
    printf("%lld\n", res + sum);
}
int main() {
    int T;
    scanf("%d", &T);
    while (T -- )   solve();
    return 0;
}