数据结构-图整理 5-04（原创）最短路径、拓扑排序、关键路径

一、最短路径（带权图内）

图的最短路径问题是在一个带权图中，寻找两个顶点之间（单源最短路径）或所有顶点对之间（多源最短路径）权重最小的路径。

1.单源最短路径(两个点)

定义：

从图中某一特定顶点（源点）出发，找出到其他各顶点的最短路径。

常用算法-Dijkstra 算法

• 适用范围：适用于边权非负的有向图或无向图。
• 原理：维护一个距离源点距离最短的顶点集合。初始时，集合仅包含源点，且源点到自身距离为 0，其他顶点距离设为无穷大。然后不断从集合外选择距离源点最近的顶点加入集合，并利用新加入顶点更新集合外其他顶点到源点的距离，直到所有顶点都加入集合。
• 时间复杂度：朴素实现为O(n^2)，使用优先队列优化后可达O((n+E)logn)，其中n是顶点数，E是边数。
• 

使用dijkstra算法画出表格并求出最短路径Dist[]

总结：

• 从源点开始，先写出到各点的距离Dist[]，无法到达就记为none,Path路径记录的是最短路径下的上一结点，无法到达记为-1。
• 选择距离源点最近的顶点加入集合s中（同时删去u中，便于之后减少判断量），作为新的源点更新距离Dist[]和path路径，然后循环上一步骤即可。

例题1：

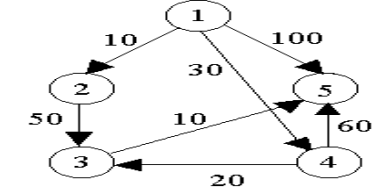
用Dijkstra算法计算源点1到各顶点的最短路径及路径长度

1.将下表填写完整。注意：Na代表不可到达，0代表到源点自己的距离为0。

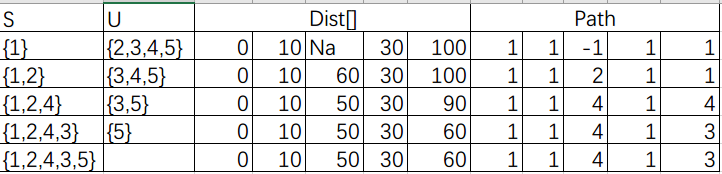
2.写出1号顶点到其他顶点的最短路径长度（根据path）及最短路径序列（根据path逆推）

1到2的最短路径长度：10，路径序列：1,2

1到3的最短路径长度：50，路径序列：1,4,3

1到4的最短路径长度：30，路径序列：1,4

1到5的最短路径长度：60，路径序列：1,4，3，5

例题2：

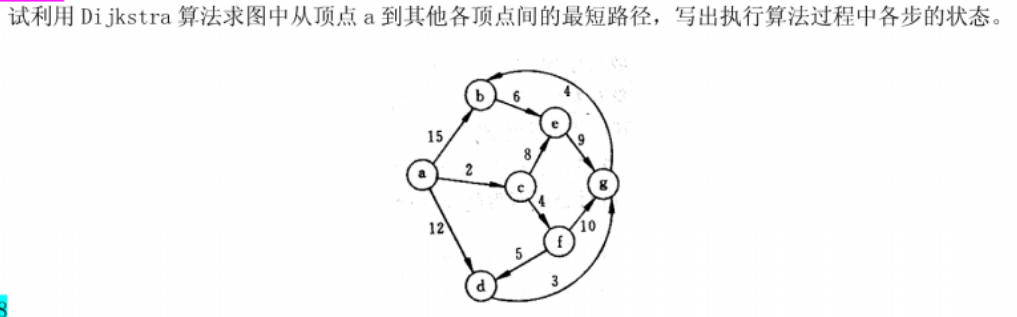
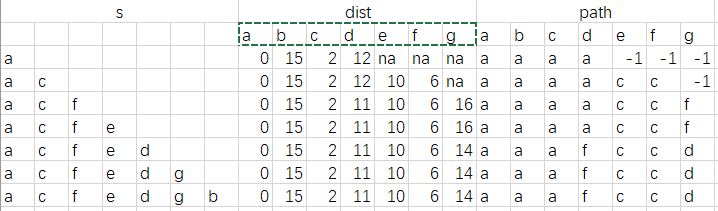
例题3：

本题要求给出下图中从A到其他顶点的最短路径。

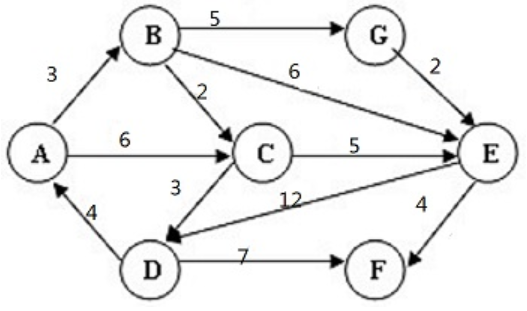
这题讲一下直接看图的方法，由于已经给出部分最短路径，所以找a到其所有前结点的最短路径再加上到该点的距离然后比较就可以得到最短路径

比如对e，前结点有b、c、g，然后b(min)= 3,c(min)=ABC=5,g=ABG=8,

因为ABE=9<ABCE=10=ABGE所以E最短路径为ABE

（这里ac最短路径应该是ABC，题目给错了）

例题4：

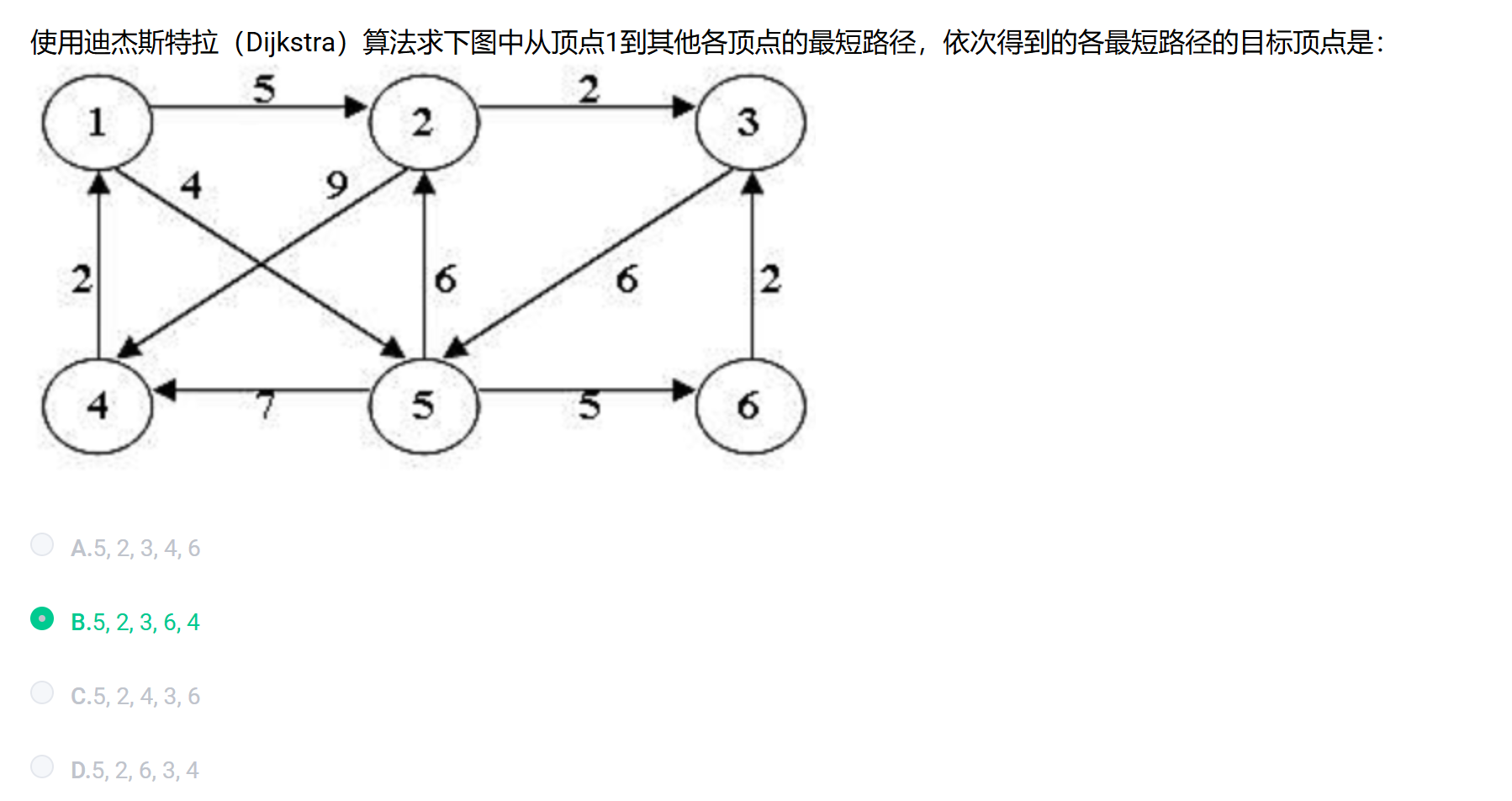
s	dist	path

						1	2	3	4	5	6	1	2	3	4	5	6
1						0	5	na	na	4	na	1	1	-1	-1	1	-1
1	5					0	5	na	11	4	9	1	1	-1	5	1	5
1	5	2				0	5	7	11	4	9	1	1	2	5	1	5
1	5	2	3			0	5	7	11	4	9	1	1	2	5	1	5
1	5	2	3	6		0	5	7	11	4	9	1	1	2	5	1	5
1	5	2	3	6	4	0	5	7	11	4	9	1	1	2	5	1	5

2.多源最短路径（all顶点对）

定义：计算图中所有顶点对之间的最短路径。

常用算法 - Floyd 算法

• 适用范围：适用于有向图和无向图，可处理负权边，但不能处理存在负权回路的图。
• 原理：借助一个三层嵌套循环，通过不断引入中间顶点来更新任意两个顶点之间的最短路径。其核心思想是对于每一个顶点k ，判断是否可以通过顶点k ，使顶点i到顶点j的路径更短。
• 时间复杂度：O(V3) 。
• 

二、拓扑排序(有向无环图)

定义

拓扑排序是对有向无环图（DAG）的顶点进行排序，使得对于图中的任意一条有向边(u,v) ，顶点u在排序序列中都位于顶点v之前。它主要用于解决具有依赖关系的任务调度等问题，比如课程先修关系、任务执行先后顺序等。

实现算法

深度优先搜索（DFS）算法

• 原理：对图进行深度优先遍历。在回溯阶段（即从递归调用返回时 ）将顶点加入结果列表。遍历结束后，将结果列表反转，得到的序列就是拓扑排序结果。在遍历过程中，如果发现某个顶点已经在当前递归路径中被访问过，说明图中存在环，无法进行拓扑排序。
• 时间复杂度：时间复杂度为 O(V+E) 。因为对图进行深度优先遍历，每个顶点和边都只会被访问一次。

所以：

使用DFS，每访问一点查看其是否已访问过。如果已访问过则代表该有向图包含回路

1.分析时间复杂度

对于n个顶点、e条弧的有向图来说，拓扑排序有三步：
1. 建立求各顶点的入度的时间复杂度为O(e)；
2. 建零入度顶点栈的时间复杂度为O(n)；
3. 在拓扑排序过程中，若有向图无环，则每个顶点进一次栈、出一次栈，入度减1的操作在while语句中总共执行e次，所以总的时间复杂度为O(n+e)。

具体分析：
1. 拓扑排序初始参数只有邻接表，所以第一步建立入度数组，因为每一入度对应一条弧，总共e条弧，建立入度数组的复杂度为O(e)。
2. 每个节点入一次栈、出一次栈，也就是每个节点输出一次。那么就要遍历n个节点，因此时间复杂度为O(n)。（使用零入度节点栈的原因是，如果不把零入度节点入栈，每次输出时都要遍历节点。建立此栈，只需遍历一次。）
3. 然后对每个节点进行入度减1的操作，也是一条弧对应一次，e条弧总共O(e)。以上总计O(n+2e)即O(n+e)。
即对每条弧要建立入度数组操作和删除操作，每个顶点要遍历一次并删除。故时间复杂度为O(n+e)。

2.判断拓扑序列

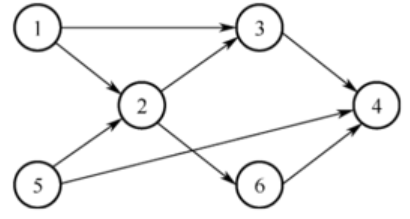
3.判断题

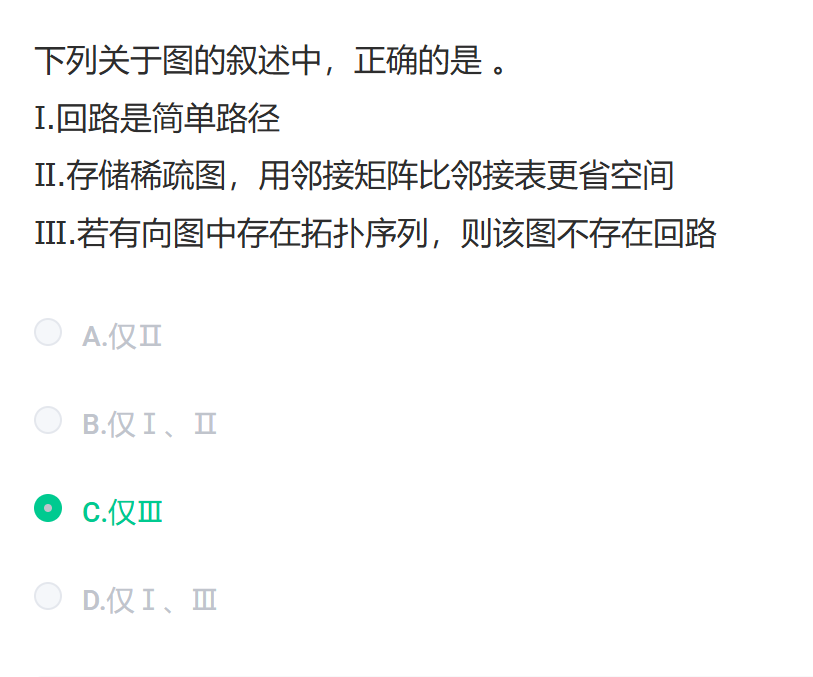
顺带复习一下前面的知识

Ⅰ：简单路径是指在路径中顶点不重复出现的路径 ，而回路是起点和终点为同一个顶点的路径，必然存在顶点重复，所以回路不是简单路径，Ⅰ 错误。
Ⅱ：邻接矩阵表示图时，空间复杂度为O(V2)（V为顶点数） ，不管图是稀疏还是稠密，都需要这么大空间。邻接表表示图时，空间复杂度为O(V+E)（E为边数），对于稀疏图（E≪V2 ），邻接表比邻接矩阵更省空间，Ⅱ 错误。
Ⅲ：拓扑排序是对有向无环图的顶点进行排序，若有向图中存在拓扑序列，说明该图不存在回路（有回路的图无法进行拓扑排序），Ⅲ 正确。

三、关键路径（有向无环图的最长路径）

AOE 网（Activity On Edge Network）即边表示活动的网络，是一个带权的有向无环图（DAG）。

综合题

先画出图对应的上三角（对角线往上）邻接矩阵（一维数组以结点数-1记录）为：

（1）画出有向带权图G。

（2）写一个拓扑序列

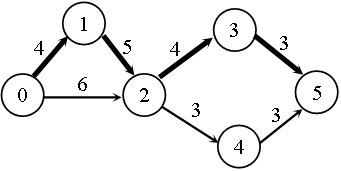
（3）画图G的关键路径，并计算该关键路径的长度。

1.画出有向图

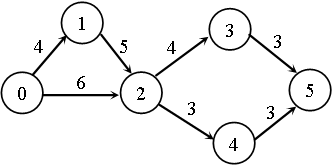
2.拓扑序列（注意1要在2的前面）：

0 1 2 3 4 5

3.关键路径（最长的）=16